Capitolo 8 Verifica dei modelli

Nei capitoli precedenti, abbiamo studiato i modelli come “strumenti” per descrivere le relazioni causa-effetto tra le variabili sperimentali e per trarre conclusioni testando ed eventualmente rigettando ipotesi scientifiche rilevanti. Tuttavia, abbiamo anche visto che i modelli statistici e le inferenze su di essi basate, assumono che siano verificate alcune condizioni fondamentali:

1. il modello fornisce una buona descrizione dei dati sperimentali (bontà di adattamento);
2. i residui sono indipendenti l’uno dall’altro (indipendenza);
3. i residui hanno una distribuzione gaussiana di probabilità (normalità);
4. tutti i residui hanno la stessa varianza (omoschedasticità).

Oltre alle ipotesi di cui sopra, i dati osservati devono rispettare anche un altro requisito essenziale: l’assenza di valori anomali (outliers), ovvero osservazioni che differiscono notevolmente da tutte le altre osservazioni nello stesso gruppo di trattamento. Questi valori anomali producono residui negativi o positivi enormi, che possono essere molto influenti, sia per il test d’ipotesi che per l’affidabilità delle stime.

Purtroppo, bisogna riconoscere che i problemi relativi alle assunzioni di base sono tutt’altro che infrequenti, come vedremo in seguito.

8.1 Deviazioni rispetto alle assunzioni di base

La mancanza di ‘bontà d’adattamento’ (più semplicemente: ‘mancanza d’adattamento’) può verificarsi quando le previsioni del modello sembrano deviare sistematicamente rispetto ai dati osservati, ad esempio quando una modello di regressione lineare viene adattato ad una risposta curvilinea. In caso di mancanza di adattamento, dovremo concludere che i dati e il modello non si supportano a vicenda e, quindi, che il modello “non consente al ricercatore di rispondere alle sue domande scientifiche” (Kass et al., 2016).

La mancanza d’indipendenza dei residui del modello può verificarsi a causa di:

1. intrusioni sistematiche,
2. presenza di fattori di raggruppamento non considerati nel modello,
3. mancanza di adattamento sistematica dovuta alla selezione errata del modello, o
4. mancanza di randomizzazione adeguata (vedere anche Sezione 4.6 e Capitolo 12).

La mancanza di indipendenza è considerata una delle assunzioni di base più pericolose da violare, poiché comporta un rischio elevato di errore di I specie (Frey et al., 2024), ovvero un rischio maggiore di rifiutare erroneamente un’ipotesi nulla vera (falso positivo).

La normalità viene violata quando i residui del modello non “riflettono” la forma tipica di una distribuzione gaussiana, ovvero quando sono asimmetrici (distribuzione asimmetrica: la media non è uguale alla mediana) o quando le code sono troppo ‘alte’ (distribuzione platicurtica: troppi valori estremi) o troppo ‘basse’ (distribuzione leptocurtica: i valori sono troppo “concentrati” attorno alla media)(Fig. 8.1). In assenza di outliers (vedi più avanti), la non normalità è considerata meno dannosa di altre deviazioni (Knief e Forstmeier, 2021), in quanto non provoca forti distorsioni nella stima dei parametri od un incremento del rischio di errore di I specie. Tuttavia, si raccomanda sempre un atteggiamento cauto, poiché le deviazioni dalla normalità possono essere associate ad altri tipi di deviazioni più pericolose, come l’eteroschedasticità. Deviazioni dalla normalità possono verificarsi anche a causa della presenza di outliers, collegati ad errori casuali di entità eccezionale (ad esempio, procedure difettose, scarso controllo o intrusioni di qualsiasi tipo). Questi outliers modificano profondamente medie e deviazioni standard, portando ad un’errata interpretazione dei risultati sperimentali (Cochran, 1947).

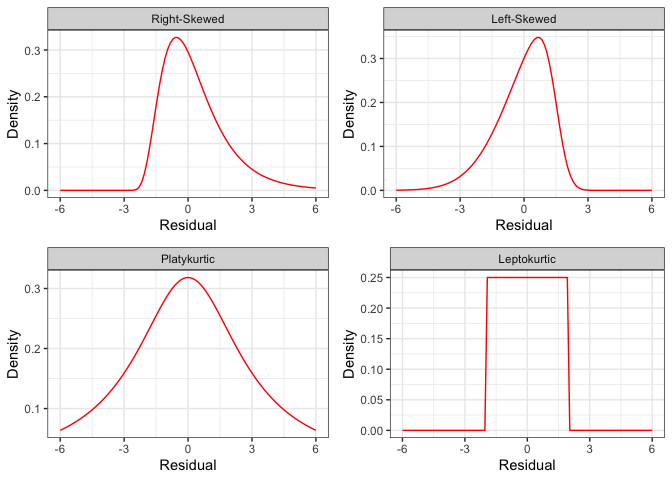
Figura 8.1: Alcune distribuzioni non-normali dei residui.

L’eteroschedasticità può verificarsi, ad esempio, quando i trattamenti sperimentali producono effetti sia sulla media che sulle deviazioni standard (ad esempio, effetti moltiplicativi) in modo tale che queste due statistiche diventino proporzionali tra loro (quando la media aumenta, aumenta proporzionalmente anche la deviazione standard). Altre cause comuni di eteroschedasticità includono attacchi di parassiti e altre intrusioni, nonché un grado inferiore di controllo in alcune parti dell’esperimento di campo. È stato dimostrato che l’eteroschedasticità si traduce in una stima distorta della deviazione standard dei residui e porta a P-value non validi, così che il reale rischio d’errore di I specie può essere anche molto diverso da quello nominale (Glass et al., 1972).

8.2 Scoprire le violazioni

Il rispetto di alcune assunzioni di base, come l’indipendenza dei residui e l’assenza di errori sistematici, è garantito dall’adozione di un disegno sperimentale a ‘regola d’arte’, cioè basato su repliche indipendenti e correttamente randomizzate. Bisogna tenere presente che gli eventuali vincoli alla randomizzazione introdotti in fase di disegno sperimentale (blocchi randomizzati, quadrato latino, split-plot…) possono inficiare l’indipendenza dei residui; ad esempio, con i blocchi randomizzati, le osservazioni all’interno dello stesso blocco si assomigliano di più che non quelle in blocchi diversi, proprio perché condividono le condizioni ambientali caratteristiche di ciascun blocco. Insomma, si realizza un certo grado di ‘parentela’ tra le osservazioni, che non è compatibile con l’ipotesi di totale indipendenza. Vedremo nei capitoli successivi che queste situazioni vengono gestite includendo nel modello ANOVA anche il fattore di blocco o gli altri vincoli eventualmente imposti alla randomizzazione completa.

Per quanto riguarda le altre assunzioni di base, come la bontà di adattamento, l’omogeneità delle varianze e la normalità dei residui, la verifica può essere fatta solo a posteriori, cioè dopo aver effettuato la stima dei parametri ed aver individuato i residui stessi.

Oltre a quanto abbiamo finora dotto, dobbiamo anche tener presente che il dataset non dovrebbe contenere le cosiddette osservazioni aberranti od outliers. Si tratta di osservazioni molto diverse dalle altre, che spesso fanno sospettare che sia avvenuto qualche errore grossolano; la loro assenza non è postulata da alcun modello statistico, anche se esse, proprio perché molto diverse dalle altre, finiscono per inficiare la normalità dei residui e l’omogeneità delle varianze, oltre a stravolgere pericolosamente le nostre conclusioni. Pertanto, alla loro individuazione deve essere sempre dedicata la debita attenzione.

Per diagnosticare eventuali problemi con le assunzioni di base e/o con la presenza di outliers, possiamo utilizzare sia metodi grafici che metodi formali, basati sul test d’ipotesi. Vediamo ora alcune possibilità.

8.3 Analisi grafica dei residui

Dato che la gran parte delle assunzioni riguarda la struttura dei residui, l’ispezione grafica di questi ultimi è in grado di evidenziare chiaramente la gran parte dei problemi e dovrebbe, pertanto, essere considerata come una metodica da applicare in modo routinario. Esistono diversi tipi di grafici, ma ne elenchiamo fondamentalmente due: il grafico dei residui contro i valori attesi e il QQ-plot.

8.3.1 Grafico dei valori osservati, aumentato con le previsioni del modello

Per tutti i tipi di modelli di regressione, lo strumento più importante per verificare la bontà di adattamento è un grafico a dispersione della risposta osservata rispetto al predittore, integQuest’ultima dovrebbe seguire fedelmente i dati osservati (Fig. 8.2A) senza mostrare alcun segno di deviazioni sistematiche, come illustrato nelle Figure 8.2B, C e D.

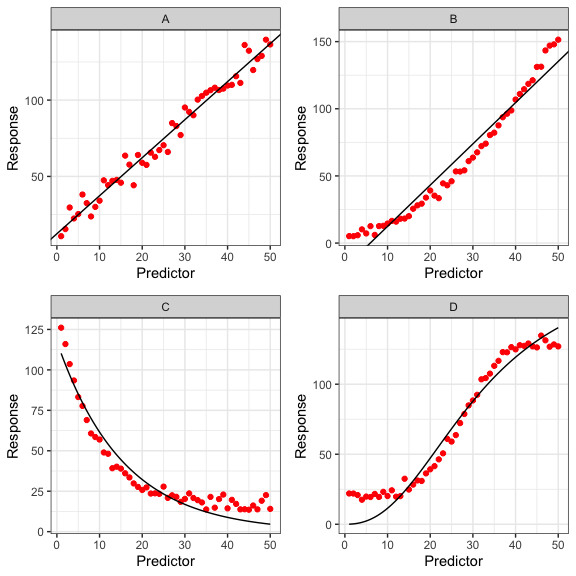
Figura 8.2: Grafico a dispersione delle risposte osservate (simboli), integrati con le previsioni del modello (linee e curve). Il panel in alto a sinistra mostra un modello con un buon adattamento, mentre gli altri grafici mostrano diversi tipi di violazioni.

8.3.2 Grafico dei residui contro i valori attesi

Il metodo grafico più utilizzato per l’analisi dei residui consiste nel plottare i residui stessi contro i valori attesi. Se non vi sono problemi, i punti nel grafico dovrebbero essere distribuiti in modo assolutamente casuale, come in Figura 8.3, in alto a sinistra. Le osservazioni aberranti (outliers) appaiono invece come punti isolati rispetto agli altri (Fig. 8.3; in alto a destra). L’eterogeneità delle varianze è invece indicata da residui che si allargano o si stringono procedendo verso i margini del grafico (Figura 8.3, in basso a sinistra), facendo emergere una sorta di proporzionalità tra media e varianza. In ultimo, la mancanza di adattamento nei modelli di regressione è evidenziata da un qualche evidente pattern, come quando i residui sono tendenzialmente negativi per bassi valori attesi e positivi per alti valori, chiaro segnale di un modello deterministico che sovrastima le osservazioni quando sono basse e le sottostima quando sono alte (Fig. 8.3; in basso a destra).

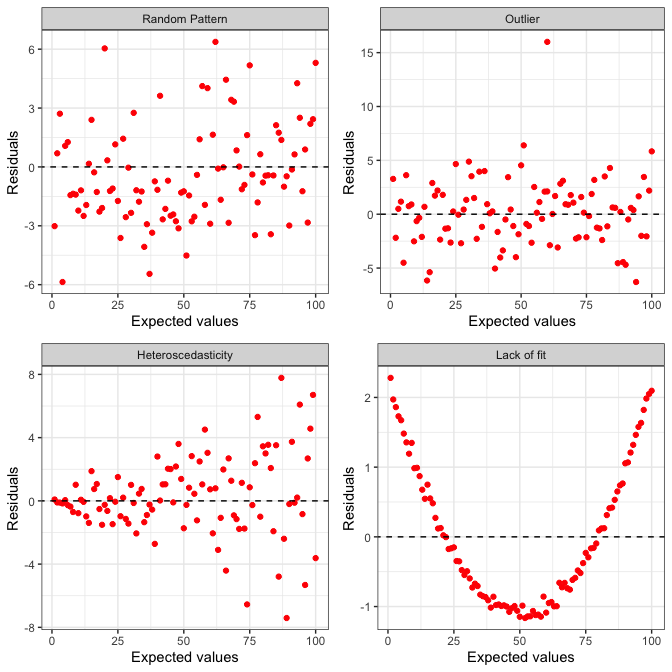
Figura 8.3: Plot dei residui contro i valori attesi: una disposizione dei punti totalmente casuale supportata l’ipotesi che le assunzioni di base siano rispettate (in alto a sinistra). Gli outliers sono evidenziati come punti ‘isolati’ (in alto a destra), mentre una disposizione ad ‘imbuto’ rivela che le varianze sono direttamente o inversamente proporzionali alle medie (in basso a sinistra). La mancanza d’adattamento è invece rivelata da un qualkunque evidente pattern nella disposizione dei punti, come, ad esempio, dei residui associati di ugual segno in una certa zona del grafico (in basso a destra).

8.3.3 QQ-plot

Per evidenziare problemi di non-normalità, risulta molto utile un QQ-plot (quantile-quantile plot), nel quale i residui standardizzati vengono ‘plottati’ contro i rispettivi percentili di una distribuzione normale standardizzata. Con residui normali, queste due entità (i residui standardizzati e i percentili corrispondenti di una distribuzione normale standardizzata) sono largamente coincidenti, in modo che i punti nel QQ-plot giacciono lungo la bisettrice del primo e del terzo quadrante (8.4 in alto a sinistra).

Le deviazioni più diffuse dalla normalità sono relative alla simmetria (skewness) e alla curtosi della popolazione da cui i residui sono campionati. In particolare, può capitare che i residui provengano da una popolazione con asimmetria positiva (right-skewed), come, ad esempio, una popolazione log-normale. In questo caso, la media è maggiore della mediana e i residui negativi sono più numerosi, ma più piccoli in valore assoluto di quelli positivi. Il QQ-plot si presenta come in figura 8.4 in alto al centro. Al contrario, se i residui provengono da una popolazione con asimmetria negativa (‘left-skewed’), caratterizzata, ad esempio, da una funzione di densità ‘beta’, la media è minore della mediana e, di conseguenza, i valori positivi sono più numerosi, ma più vicini allo zero di quelli negativi. In questa situazione, il QQ-plot presenta un andamento abbastanza tipico, come indicato in Figura 8.4 in alto a destra.

Per quanto riguarda la curtosi, è necessario osservare le code della distribuzione: se queste sono più alte di una distribuzione normale parliamo di distribuzione platicurtica, mentre se sono più basse parliamo di distribuzione leptocurtica. Ad esempio, se i residui provengono da una distribuzione t di Student con pochi gradi di libertà sono platicurtici ed il QQ-plot mostra l’andamento indicato in figura 8.4 in basso a sinistra. Al contrario, se i residui provengono da una distribuzione uniforme sono tipicamente leptocurtici e presentano un QQ-plot come quello riportato in Figura 8.4 in basso al centro.

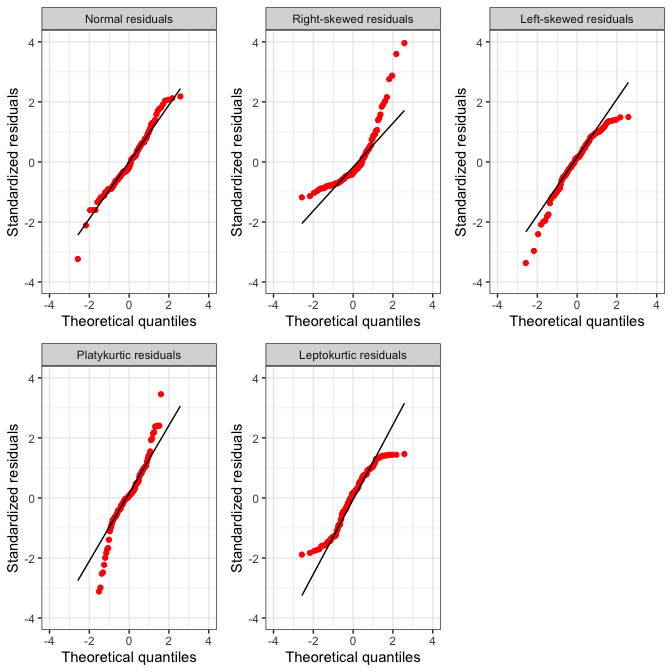
Figura 8.4: QQ-plot per residui gaussiani (in alto a sinistra) e per residui che mostrano diversi tipi di violazioni dalla normalità (vedi anche Fig. 8.1).

8.4 Test d’ipotesi

La valutazioni illustrate in precedenza sono basate sulla semplice osservazione di uno o più grafici, ma sono considerate sufficientemente attendibili per la maggior parte delle situazioni. Tuttavia, esistono anche test statistici formali che consentono di saggiare l’ipotesi nulla di ‘assenza di deviazioni’, che può essere rifiutata qualora il P-level fosse inferiore a 0.05.

Rispetto alle procedure grafiche, il test d’ipotesi formale può dare una miglior sensazione di obiettività, anche se non è tutto oro quel che luccica. Infatti, questi test possono creare più problemi di quanti ne risolvano dato che, ad esempio, richiedono campioni di grandi dimensioni e fanno affidamento su assunzioni di base molto stringenti, tanto che, alla fine, l’affidabilità dei risultati è spesso discutibile (Kozak e Piepho 2018). Per questi motivi, il loro utilizzo è sconsigliato e dovrebbe essere riservato a supportare situazioni complesse in cui i metodi grafici non forniscono risposte sufficientemente chiare.

Le procedure presentate in questo capitolo sono state selezionate perché ampiamente utilizzate e facilmente disponibili in R.

8.4.1 Test di Levene per l’omogeneità delle varianze

Secondo gli studi di Conover et al. (1981), il test di Levene è una delle procedure più affidabili per saggiare l’ipotesi di omoschedasticità nei modelli con predittori nominali; consiste nel’eseguire l’analisi della varianza di una ‘pseudo-risposta’, ottenuta sostituendo ciascun dato osservato con il valore assoluto della sua differenza con il centro del gruppo a cui appartiene (dati ‘group-centered’).

Inizialmente, Levene propose di utilizzare come centro di gruppo la media; l’idea di fondo era che, sebbene le medie di gruppo di dati ‘group-centered’ siano pari a zero, prendendo i valori assoluto (cioè rimuovendo i segno negativi), queste medie diventano diverse da zero e sono tanto più alte quanto più la varianza di gruppo è alta. Questo concetto sarà più semplice da comprendere utilizzando un esempio pratico. Consideriamo due gruppi sperimentali A <- c(19, 20, 21) e B <- c(26, 30, 34), che hanno, rispettivamente, medie pari a 20 e 30, e varianze pari a 1 e 16. Sottraendo dalle osservazioni di ogni gruppo la media del gruppo stesso, otteniamo le pseudo-osservazioni Ac <- c(-1, 0, 1) e Bc <- c(-4, 0, 4), la cui media è zero, mentre le varianze restano inalterate. Se escludiamo i segno negativi, le medie dei due gruppi divengono pari, rispettivamente, a 2/3 e 8/3, mostrando come il gruppo con più alta varianza abbia prodotto pseudo-osservazioni con media più alta. Se la differenza tra le due medie delle pseudo-osservazioni è significativa, l’ipotesi nulla di omogeneità delle varianze può essere rigettata.

Lavori successivi (Brown e Forsythe, 1974) hanno mostrato che è preferibile sostituire la media del gruppo con la sua mediana, per ottenere un test più robusto per dati non normali.

Sia il test di Levene che il test di Brown-Forsythe sono disponibili nella funzione leveneTest() del package car, ma il secondo è largamente preferito e considerato come la procedura di ‘default’. Un esempio di questo test è fornito nel Riquadro 8.3, che confronta due genotipi di mais in un disegno completamente randomizzato con 11 repliche. Il secondo genotipo (B) presenta una varianza maggiore e il test di Levene risulta significativo (il valore P è inferiore a 0,05 e l’ipotesi nulla di omoschedasticità viene rifiutata). I due test (centrato sulle medie o centrato sulle mediane) producono risultati simili, il che potrebbe suggerire che i dati originali non si discostino significativamente dalla normalità.

# Code Box 8.1
# Testing hypotheses about model residuals
# Levene’s test for homoscedasticity
library(car)

# Entering the data
dataset <- data.frame(Genotype = c("A", "A", "A", "A", "A",
                                   "A", "A", "A", "A", "A",
                                   "A", "B", "B", "B", "B",
                                   "B", "B", "B", "B", "B",
                                   "B", "B"),
                      Yield = c(10.0, 10.7, 11.9, 10.3, 10.0,
                                7.8, 10.4, 9.7, 10.0, 9.2, 9.7,
                                15.0, 11.2, 13.7, 11.9, 9.4,
                                10.6, 12.6, 10.1, 9.9, 15.3, 12.2))
head(dataset)
##   Genotype Yield
## 1        A  10.0
## 2        A  10.7
## 3        A  11.9
## 4        A  10.3
## 5        A  10.0
## 6        A   7.8
dataset$Genotype <- factor(dataset$Genotype)

# Fitting the model
mod <- lm(Yield ~ Genotype, data = dataset)

# Centering the data by subtracting, for each genotype 
# the group mean (Levene’s test)
GroupMeans <- tapply(dataset$Yield, dataset$Genotype, mean)
YieldC <- dataset$Yield - rep(GroupMeans, each = 11)

# Re-fitting the same model to the absolute values of 
# centered data and run an ANOVA
modlevene <- lm(abs(YieldC) ~ dataset$Genotype)
anova(modlevene)
## Analysis of Variance Table
## 
## Response: abs(YieldC)
##                  Df  Sum Sq Mean Sq F value  Pr(>F)  
## dataset$Genotype  1  5.2129  5.2129  5.8944 0.02475 *
## Residuals        20 17.6878  0.8844                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Centering the data by subtracting, for each genotype
# the group median (Brown-Forsythe’s test)
GroupMedians <- tapply(dataset$Yield, dataset$Genotype, median)
YieldC <- dataset$Yield - rep(GroupMedians, each = 11)

# Re-fitting the same model to the absolute values of # centered data and run an ANOVA
modlevene <- lm(abs(YieldC) ~ dataset$Genotype)
anova(modlevene)
## Analysis of Variance Table
## 
## Response: abs(YieldC)
##                  Df  Sum Sq Mean Sq F value  Pr(>F)  
## dataset$Genotype  1  5.2041  5.2041  5.7245 0.02666 *
## Residuals        20 18.1818  0.9091                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Non-robust Levene’s test with R (centering with means)
leveneTest(mod, center = "mean")
## Levene's Test for Homogeneity of Variance (center = "mean")
##       Df F value  Pr(>F)  
## group  1  5.8944 0.02475 *
##       20                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Levene’s test with R (centering with medians; default)
leveneTest(mod)
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value  Pr(>F)  
## group  1  5.7245 0.02666 *
##       20                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

8.4.2 Test di Shapiro-Wilk per la normalità

Il test di Shapiro-Wilk per la normalità fornisce la statistica W e un valore P per l’ipotesi nulla che i residui siano distribuiti normalmente. La procedura di test non è così semplice come quella del test di Levene e i calcoli manuali non sono altrettanto facili da eseguire. Tuttavia, possiamo utilizzare la funzione shapiro.test() in R, passando i residui del modello come argomento (vedi l’esempio seguente).

8.4.3 Altri test

Vale la pena menzionare alcune tecniche numeriche per l’individuazione di valori anomali, come i metodi proposti da Anscombe e Tukey (1963) e Grubbs (1969).

8.5 Esempio 8.1: Analisi dei residui per il dataset “mixture”

Abbiamo eseguito un esperimento in vaso, nel quale abbiamo utilizzato quattro trattamenti erbicidi:

1. Metribuzin
2. Rimsulfuron
3. Metribuzin + rimsulfuron
4. Testimone non trattato

Lo scopo dell’esperimento era quello di verificare se la miscela metribuzin e rimsulfuron è più efficace dei due componenti utilizzati separatamente.

A questo fine, sono stati preparati sedici vasi uniformi e sono stati seminati con Solanum nigrum, un importante infestante di alcune colture primaverili estive, come mais e pomodoro. Quando le piante hanno raggiunto lo stadio di 4 foglie vere, sono state trattate con una delle tesi sopra elencate, secondo un disegno sperimentale completamente randomizzato con quattro repliche. Tre settimane dopo i trattamenti, le piante in ciascun vaso sono state raccolte e pesate; minore era il peso, maggiore era l’efficacia degli erbicidi (Onofri et al. 1995).

Per questo esperimento, è possibile adattare un modello lineare con un predittore nominale (il trattamento erbicida) (vedere Eq. 4.6 nel Cap. 4), come mostrato nel riquadro sottostante.

# Code box 8.2
# Example 8.1
# Checking the residuals for the `mixture' data

# Loading the packages
library(statforbiology)
library(car)

# Loading and transforming the data
mixture <- getAgroData("mixture")
mixture$Treat <- factor(mixture$Treat)
head(mixture)
##             Treat Weight
## 1 Metribuzin__348  15.20
## 2 Metribuzin__348   4.38
## 3 Metribuzin__348  10.32
## 4 Metribuzin__348   6.80
## 5     Mixture_378   6.14
## 6     Mixture_378   1.95
# Model fitting
mod1 <- lm(Weight ~ Treat, data = mixture)

Dopo aver effettuato la stima dei parametri, i grafici dei residui possono essere ottenuti utilizzando la funzione plot() applicata al risultato del fitting lineare. L’argomento ‘which’ specifica il tipo di grafico: se utilizziamo: ‘which = 1’ otteniamo il grafico dei residui verso gli attesi, se invece utilizziamo ‘which = 2’ otteniamo il QQ-plot. I due comandi sono:

plot(mod, which = 1)
plot(mod, which = 2)

e il risultato è mostrato nella figura 8.5.

Figura 8.5: Analisi grafica dei residui per un modello ANOVA ad una via adattato al dataset ‘mixture.csv’

Nessuno dei grafici suggerisce l’esistenza di particolari problematiche e, considerando anche che che non si tratta di un conteggio o una proporzione e che le differenze tra le medie sono piuttosto piccole (meno di un ordine di grandezza), possiamo concludere che non vi sono motivi per dubitare del rispetto delle assunzioni di base.

Sebbene ciò non sia necessario, possiamo confermare la nostra conclusione eseguendo i test di Levene e Shapiro-Wilk. Nel codice sottostante possiamo notare come la funzione leveneTest() richieda come argomento l’oggetto risultante dal fitting lineare, mentre la funzione shapiro.test() richiede i residui del modello.

# Example 8.1 [continuation]

# Levene's test and Shapiro-Wilk's test
leveneTest(mod1)
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  3  1.0698 0.3984
##       12
shapiro.test(residuals(mod1))
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mod1)
## W = 0.97615, p-value = 0.9257

8.6 Esempio 8.2: Analisi dei residui per il dataset ‘insects’

Proviamo ad analizzare il dataset ‘insects’, che si riferisce ad un esperimento nel quale quindici piante sono state trattate con tre insetticidi diversi in modo completamente randomizzato, scegliendo cinque piante a caso per insetticida. Tre settimane dopo il trattamento è stato rilevato il numero di insetti presenti su ciascuna pianta.

Per testare l’effetto degli insetticidi, è stato adattato ai dati osservati un modello ANOVA ad una via, utilizzando la variabile “Insecticide” come predittore nominale. In questo caso, il controllo delle deviazioni dagli assunti di base richiede grande attenzione, poiché la variabile di risposta è un conteggio e le statistiche descrittive, che si lasciano per eercizio al lettore, indicano che le deviazioni standard sono in qualche modo proporzionali alle medie. Le analisi grafiche dei residui in Figura 8.6 mostrano chiari segni di eteroschedasticità (grafico a sinistra) e residui asimmetrici a destra (grafico a destra). Queste deviazioni sono confermate dal test di Levene (valore P = 0,043) e dal test di Shapiro-Wilks (valore P = 0,048).

# Example 8.2
# checking the residuals for the `insects' data

# Loading the packages
library(statforbiology)
library(car)

# Loading and transforming the data
insects <- getAgroData("insects")
insects$Insecticide <- factor(insects$Insecticide)
head(insects)
##   Insecticide Rep Count
## 1          T1   1   448
## 2          T1   2   906
## 3          T1   3   484
## 4          T1   4   477
## 5          T1   5   634
## 6          T2   1   211
# Fitting a model
mod2 <- lm(Count ~ Insecticide, data = insects)

# Graphical analyses of residuals (not run, see Figure)
# plot(mod2, which = 1)
# plot(mod2, which = 2)

# Levene's test
leveneTest(mod2)
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  1.0263 0.3878
##       12
# Shapiro-Wilks' test
shapiro.test(residuals(mod2))
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mod2)
## W = 0.87689, p-value = 0.04265

Figura 8.6: Analisi grafica dei residui per il dataset ‘insects.csv’

8.7 Misure correttive

Se le procedure diagnostiche hanno evidenziato deviazioni rispetto agli assunti di base, è necessario valutare se e come intraprendere azioni correttive. Ovviamente, la ‘terapia’ cambia al cambiare della ‘patologia’.

8.7.1 Correzione/Rimozione degli outliers

In presenza di outliers, la ‘terapia’ più opportuna è, banalmente, quella di rimuoverli, ottenendo così un dataset ‘sbilanciato’ (diverso numero di repliche per trattamento). Oggigiorno, trattare un dataset sbilanciato non costituisce un problema, ovviamente se si utilizzano le metodiche di analisi opportune. Qualche anno fa, al contrario, si cercava di evitare lo sbilanciamento a tutti i costi, utilizzando tecniche di imputing per l’immissione di valori ‘ragionevoli’ in sostituzione di quelli mancanti/aberranti. Con le dovute eccezioni, le tecniche di imputing sembrano oggi abbastanza obsolete, almeno in questo contesto.

Vorremmo porre l’attenzione sul fatto che i dati aberranti possono influenzare in modo molto marcato il risultato dell’analisi (sono dati ‘influenziali’); pertanto, se è sbagliato correggerli arbitrariamente, senza aver prima accertato che siano effettivamente frutto di errore, può essere altrettanto sbagliato lasciarli nel dataset. Ovviamente, la rimozione non può che riguardare una larga minoranza dei dati sperimentali raccolti, altrimenti si dovrà necessariamente pensare di ripetere l’esperimento.

8.7.2 Correzione del modello

Abbiamo visto che il modello impiegato potrebbe non essere adatto a descrivere il dataset (mancanza di adattamento). Gli effetti potrebbero non essere additivi, ma moltiplicativi, oppure potrebbero essere non-lineari. Potrebbero essere presenti asintoti che il nostro modello non è in grado di descrivere, oppure la crescita/decrescita osservata potrebbero essere più lente/veloci di quanto la nostra funzione sia in grado di descrivere. Per tutti questi casi, ovviamente, la strategia più consigliabile è quella di utilizzare un diverso modello, capace di descrivere meglio le osservazioni sperimentali.

8.7.3 Trasformazione del predittore

Quando il predittore è quantitativo e la risposta sembra non essere lineare è possibile trasformare il predittore stesso in modo da linearizzare la risposta. Ad esempio, se la risposta mostra un andamento esponenziale, la trasformazione del predittore in logaritmo può portare al sensibile miglioramento del fitting con un’equazione lineare. Vedremo un esempio di questa tecnica in un capitolo successivo.

8.7.4 Trasformazione della risposta

Una strategia empirica, ma molto semplice, diffusa ed efficace, è quella di ricorrere alle trasformazioni correttive. Con questa tecnica, si trasformano i dati in modo da portarli su una metrica che soddisfi le assunzioni di base dei modelli lineari; successivamente si ripete l’elaborazione sui dati trasformati.

Le trasformazioni possibili sono molte: ad esempio, i libri di testo più tradizionali (esempio: Snedecor e Cochran, 1991) consigliano la trasformazione in radice quadrata per i conteggi, la trasformazione angolare (arcoseno della radice quadrata) per le percentuali e la trasformazione in logaritmo per i dati log-normali, dove le variance sono proporzionali alle medie.

Per evitare di scegliere la trasformazione ‘al buio’, si può impiegare la procedura suggerita da Box e Cox (1964), basata su una ‘famiglia di trasformazioni’, così definita:

\[ W = \left\{ \begin{array}{ll} \frac{Y^\lambda - 1}{\lambda} & \quad \textrm{if} \,\,\, \lambda \neq 0 \\ \log(Y) & \quad \textrm{if} \,\,\, \lambda = 0 \end{array} \right.\]

dove \(W\) è la variabile trasformata, \(Y\) è la variabile originale e \(\lambda\) è il parametro che definisce la trasformazione ³

Questa famiglia è molto flessibile, nel senso che cambiando il valore di \(\lambda\) possiamo rimediare alla gran parte delle deviazioni rispetto alle assunzioni di base. Il valore ottimale (di massima verosimiglianza) per questo parametro può essere scelto con la funzione boxcox(), nel package MASS, come sarà mostrato negli esempi seguenti. Bisogna tener presente che, qualora il valore ottimale risultasse \(\lambda = 1\), la trasformazione sarebbe completamente fittizia, in quanto, da ogni dato, verrebbe semplicemente sottratta un’unità, senza quindi alterare minimamente i risultati dell’analisi. Di conseguenza, trovare che \(\lambda\) ottimale è uguale ad 1 viene considerato come evidenza del fatto che la trasformazione non è necessaria.

8.7.5 Esempio 8.1 (segue)

Sebbene le analisi precedenti abbiano mostrato che il dataset “mixture” non viola significativamente le assunzioni di base per i modelli lineari, possiamo comunque valutare la necessità di una trasformazione, utilizzando la funzione boxcox() contenuta nel package MASS e passando l’oggetto risultante dal fitting come argomento (Codice sottostante). Questa funzione restituisce un grafico delle verosimiglianze associate a diversi valori di \(\lambda\) (Fig. 8.7); il valore ottimale sarebbe \(\lambda = 0.83\), ma vediamo che anche \(\lambda = 1\) rientra nell’intervallo di confidenza di \(\lambda\) ottimale e, di conseguenza, si conferma che non è necessaria alcuna trasformazione stabilizzante.

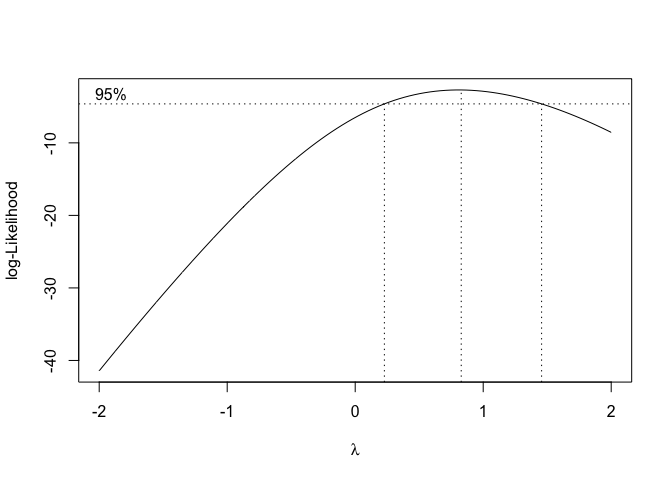
Figura 8.7: Scelta del valore ottimale di ‘lambda’ per la trasformazione di Box e Cox: caso in cui la trasformazione non è necessaria

8.7.6 Esempio 8.2 (segue)

Il metodo Box-Cox per il dataset “insects” restituisce il grafico in Figura 8.8; il valore di massima verosimiglianza è \(\lambda = 0.14\), e l’intervallo di confidenza del 95% va da poco meno di zero a circa 0.5. Pertanto, per semplicità, selezioniamo \(\lambda = 0\), che corrisponde a una trasformazione logaritmica. Questa scelta è motivata dal fatto che si tratta di una trasformazione molto nota e, quindi, facilmente comprensibile.

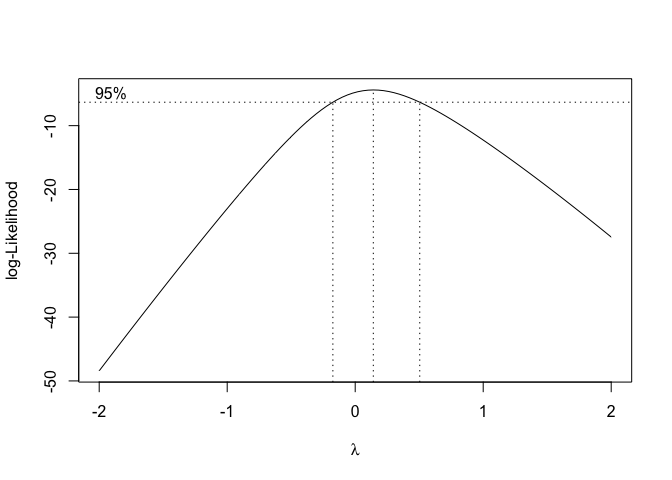
Figura 8.8: Scelta del valore ottimale di ‘lambda’ per la trasformazione di Box e Cox: caso in cui è consigliabile una trasformazione logaritmica

Il processo di analisi dei dati continua quindi trasformando i dati osservati nel loro logaritmo,e ripetendo il processo di stima del modello e sottoponendo a nuova verifica i residui risultanti. E’ importante notare nel codice sottostante come la trasformazione dei dati venga eseguita all’interno del comando di adattamento del modello, il che è utile per motivi che saranno discussi nel prossimo capitolo.

L’analisi grafica dei residui (che si lascia per esercizio) relativi ai dati trasformati non mostra più alcun sintomo di eteroschedasticità e, di conseguenza, il P-level calcolato sulla metrica logaritmica è totalmente affidabile. Procediamo quindi con l’analisi e richiediamo la tabella ANOVA, da cui si deduce che le differenze tra insetticidi sono significative (\(P = 1.49 \times 10^{−6}\). Se confrontiamo le tabelle ANOVA ottenute con e senza trasformazione, osserviamo che vi sono lievi differenze nel P-value e che, in questo caso specifico, l’analisi sui dati trasformati è leggermente più potente. Comunque, l’analisi sui dati non trasformati è sbagliata ed invalida, perché non rispetta le assunzioni di base dei modelli lineari.

# Adopting a stabilizing transformation

mod2t <- lm(log(Count) ~ Insecticide, data = insects)
anova(mod2t)
## Analysis of Variance Table
## 
## Response: log(Count)
##             Df  Sum Sq Mean Sq F value    Pr(>F)    
## Insecticide  2 15.8200  7.9100  50.122 1.493e-06 ***
## Residuals   12  1.8938  0.1578                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Comparing with ANOVA on the untransformed data
anova(mod2)
## Analysis of Variance Table
## 
## Response: Count
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## Insecticide  2 714654  357327  18.161 0.0002345 ***
## Residuals   12 236105   19675                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Concludiamo con un’osservazione pratica: nel caso in cui risultasse che il valore di \(\lambda\) ottimale è diverso sia da 1 che da 0, la trasformazione \(W = (Y^\lambda - 1)/\lambda\) potrebbe essere semplificata in \(W = Y^\lambda\), in modo da ottenere una metrica più facile da interpretare. Infatti, con \(\lambda = 0.5\) avremmo una semplice trasformazione nella radice quadrata, mentre con \(\lambda = -1\) avremmo l’altrettanto semplice trasformazione nel reciproco. Il box seguente mostra un esempio dell’equivalenza della trasformazione di Box e Cox nella forma originale e in quella semplificata: possiamo infatti notare che il rapporto F e il P-level sono esattamente uguali.

mod.1 <- lm(sqrt(Count) ~ Insecticide, data = insects)
mod.2 <- lm((Count^0.5 - 1)/0.5 ~ Insecticide, data = insects)
anova(mod.1)
## Analysis of Variance Table
## 
## Response: sqrt(Count)
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## Insecticide  2 724.22  362.11  35.022 9.791e-06 ***
## Residuals   12 124.08   10.34                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mod.2)
## Analysis of Variance Table
## 
## Response: (Count^0.5 - 1)/0.5
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## Insecticide  2 2896.9 1448.44  35.022 9.791e-06 ***
## Residuals   12  496.3   41.36                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Un’altra osservazione di cui tener conto è che la famiglia di trasformazioni di Box-Cox non funziona quando i dati sono negativi o uguali a zero. In questi casi, è possibile selezionare un valore costante, \(k\), da aggiungere alle osservazioni originali in modo che diventino strettamente positive. Ad esempio, se l’osservazione negativa più bassa è \(-0.9\), possiamo usare la trasformazione \(W = log(y + 1)\), che non produce errore in quanto non implica il calcolo del logaritmo di un numero negativo.

8.8 Risultati contraddittori

La valutazione degli assunti di base è un passo fondamentale nell’analisi dei dati sperimentali è non deve mai essere dimenticata. Tuttavia, l’esperienza insegna che, nella pratica, è molto facile incontrare situazioni dubbie, nelle quali i risultati ottenuti con le diverse tecniche diagnostiche appaiono contraddittori e difficili da interpretare. Come comportarsi in questi casi? A mio parere bisogna sempre ricordare che la ‘verità vera’ ci sfugge e, di conseguenza, tutte le valutazioni debbono essere sempre condotte con il massimo ‘buon senso’.

Un aspetto importante da considerare è la tipologia del dato: conteggi e proporzioni difficilmente sono normalmente distribuiti ed omoscedastici e, con questi dati, la prudenza non è mai troppa, quando si tratta di impiegare modelli lineari. Allo stesso modo, è necessaria una grande prudenza quando si analizzano variabili quantitative dove la differenza tra le diverse tesi è molto grande, orientativamente più di un ordine di grandezza. Con conteggi proporzioni e variabili quantitative con medie molto diverse tra loro, l’assunzione di omogeneità delle varianze è quasi sempre violata ed è quindi necessario essere molto prudenti prima di confermare il rispetto delle assunzioni di base.

8.9 Altri approcci ‘avanzati’

L’uso di trasformazioni stabilizzanti è stato molto di moda fino agli anni ’80 del ’900, quando la potenza di calcolo era estremamente bassa e rendeva possibile solo l’impiego di procedure semplici, come quelle indicate in questo libro. Oggigiorno, la diffusione di computer potenti a costo relativamente basso ha permesso la diffusione di modelli in grado di gestire anche errori non-normali e dati eteroscedastici. Questi modelli appartengono alle classi dei cosiddetti Modelli Lineari Generalizzati (GLM) o dei modelli con fitting basato sui Minimi Quadrati Generalizzati (GLS); sono molto flessibili, ma sono anche abbastanza complessi e non possono essere trattati su un testo introduttivo (potete studiare, ad esempio, Venables e Ripley, 2002).

Inoltre, per completezza di informazione, mensioneremo il fatto che esistono anche metodi di analisi dei dati che non fanno assunzioni parametriche o che ne fanno molto poche e sono, pertanto, noti come metodi non-parametrici. Non parleremo neanche di questi, rinviando chi fosse interessato alla lettura di testi specifici (esempio: Siegel e Castellan 1988).

---

8.10 Altre letture

1. Ahrens, W. H., D. J. Cox, and G. Budwar. 1990, Use of the arcsin and square root trasformation for subjectively determined percentage data. Weed science 452-458.
2. Anscombe, F. J. and J. W. Tukey. 1963, The examination and analysis of residuals. Technometrics 5: 141-160.
3. Box, G. E. P. and D. R. Cox. 1964, An analysis of transformations. Journal of the Royal Statistical Society, B-26, 211-243, discussion 244-252.
4. Brown MB, Forsythe AB (1974) Robust tests for the equality of variances. J Am Stat Assoc 69(346):364–367
5. Cochran WG (1947) Some consequences when the assumptions for the analysis of variance are not satisfied. Biometrics 3(1):22. https://doi.org/10.2307/3001535. https://www.jstor.org/stable/3001535?origin=crossref
6. Conover WJ, Johnson ME, Johnson MM (1981) A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics 23(4):351–361
7. Frey J, Hartung J, Ogutu J, Piepho H (2024) Analyze as randomized—why dropping block effects in designed experiments is a bad idea. Agron J 116(3):1371–1381. https://doi.org/10.1002/agj2. 21570. https://acsess.onlinelibrary.wiley.com/doi/10.1002/agj2.21570
8. Glass G, Peckham P, Sanders J (1972) Consequences of failure to meet assumptions underlying the fixed effects analyses of variance and covariance. Rev Educ Res 42(3):237–288
9. Grubbs FE (1969) Procedures for detecting outlying observations in samples. Technometrics 11(1):1–21
10. Kass RE, Caffo BS, Davidian M, Meng XL, Yu B, Reid N (2016) Ten simple rules for effective statistical practice. PLOS Comput Biol 12(6):e1004961. https://doi.org/10.1371/journal.pcbi. 1004961. https://dx.plos.org/10.1371/journal.pcbi.1004961
11. Knief U, Forstmeier W (2021) Violating the normality assumption may be the lesser of two evils. Behav Res Methods 53(6):2576–2590. https://doi.org/10.3758/s13428-021-01587-5. https:// link.springer.com/10.3758/s13428- 021- 01587- 5
12. Kozak M, Piepho H (2018) What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions. J Agron Crop Sci 204(1):86–98. https:// doi.org/10.1111/jac.12220. https://onlinelibrary.wiley.com/doi/10.1111/jac.12220
13. Onofri A, Covarelli L, Tei F (1995) Efficacy of rimsulfuron and metribuzin against Solanum nigrum L. at different growth stages in tomato. In: International Meeting on Weed Control. Proceedings 16th COLUMA Conference, Reims, ANPP, Reprints, pp 993–1000
14. Siegel S, Castellan NJ (1988) Nonparametric Statistics for the Behavioral Sciences. McGraw-Hill, Columbus
15. Snedecor GW, Cochran WG (1991) Statistical Methods, 8th edn. IOWA State University Press, Ames
16. Venables WN, Ripley BD (2002) Modern Applied Statistics with S. Statistics and Computing, 4th edn. Springer, New York

8.11 Esercizi

1. Considerare gli esercizi dal 5 al 7 nel capitolo 4. Per tutti questi esercizi, verificare che le ipotesi di base per i modelli lineari siano soddisfatte, utilizzando metodi grafici e test di ipotesi formali.

---

3. Nota: Considerate che il limite dell’espressione \((Y^\lambda -1)/\lambda\) per \(\lambda \rightarrow 0\) è proprio \(\log(Y)\)↩︎