Capitolo 10 Ricomponiamo il ‘puzzle’

È giunto ormai il momento di riunire tutti gli strumenti presentati nei capitoli precedenti e sviluppare un piano di lavoro per eseguire analisi dei dati corrette, produrre risultati affidabili e giungere a conclusioni pienamente supportate dai dati a nostra disposizione. Il piano di lavoro proposto non deve essere preso troppo alla lettera: è solo uno dei possibili approcci all’analisi dei dati e deve essere inteso solo come punto di partenza per ‘principianti’. Il piano di lavoro è il seguente:

Caricare i dati ed eseguire le eventuali trasformazioni che si rendano necessarie (ad es. le trasformazioni delle variabili numeriche in ‘factors’ oppure le trasformazioni stabilizzanti).
Descrivere i dati, calcolando almeno un indicatore di tendenza centrale (media) e un indicatore di variabilità (deviazione standard) come indicato nel Capitolo 3. Se necessario, utilizzare grafici per scoprire le caratteristiche principali del dataset in studio, scoprire pattern e individuare valori anomali: lasciare che i dati parlino da soli e “ascoltare” ciò che hanno da dire. Questa fase preliminare è definita Analisi Esplorativa dei Dati (EDA) ed è una parte fondamentale dell’analisi dei dati, prima dell’adattamento del modello, dell’inferenza e del test d’ipotesi.
Specificare il modello descrittivo più opportuno a stimarne i parametri con R.
Controllare il fitting per il rispetto delle assunzioni di base. Se necessario, trasformare i dati e ripetere il fitting
Calcolare gli errori standard e/o gli intervalli di confidenza e aggiungerli a tutte le stime puntuali. Verificare la significatività di tutti gli effetti tramite il test di F nell’ANOVA.
Utilizzare combinazioni lineari o non lineari dei parametri o delle medie per testare ulteriori ipotesi di interesse e rispondere a tutti i quesiti di ricerca.
Presentare i risultati sotto forma di grafici e tabelle, in modo conciso e assicurandosi di evidenziare tutte le caratteristiche chiave di interesse per il set di dati in questione.

In questo capitolo mostreremo come questo piano di lavoro possa essere messo in pratica, lavorando su alcuni dataset reali, relativi ad esperimenti agronomici di pieno campo.

10.1 Esempio 10.1: Confronto tra erbicidi in un esperimento a blocchi randomizzati

Consideriamo un esperimento di campo per confrontare otto genotipi di frumento, disegnato a blocchi randomizzati con tre repliche, nella collina Umbra durante la stagione di semina 2002 (Ciriciofolo, 2004; pubblicato in Belocchi et al. 2003). La variabile di risposta è la resa (in tonnellate per ettaro) e il set di dati è disponibile come “WinterWheat2002” nel package statforbiology. La variabile “blocco” deve essere trasformata in un fattore prima dell’analisi, altrimenti, R stimerebbe erroneamente un modello di regressione lineare (mentre i blocchi sono classi nominali e non ordinate). Anche la variabile “genotipo” può essere trasformata in un fattore, sebbene ciò sia facoltativo, poiché i genotipi non sono rappresentati con numeri. L’EDA rivela che i genotipi, ad eccezione di Simeto, sono relativamente simili in termini di resa media. Allo stesso tempo, esistono alcune differenze in termini di deviazione standard, che potrebbero giustificare un attento controllo di eteroschedasticità.

# Example 10.1
# A genotype experiment in blocks

# Loading the packages
library(statforbiology)
library(MASS)
library(car)
library(emmeans)
library(multcomp)

# Loading the 'WinterWheat2002' dataset and performing an EDA
dataset <- getAgroData("WinterWheat2002")
head(dataset)
##   Plot Block Genotype Yield
## 1   57     A COLOSSEO  4.31
## 2   61     B COLOSSEO  4.73
## 3   11     C COLOSSEO  5.64
## 4   60     A    CRESO  3.99
## 5   10     B    CRESO  4.82
## 6   42     C    CRESO  4.17
dataset$Block <- factor(dataset$Block)
dataset$Genotype <- factor(dataset$Genotype)

with(dataset, data.frame(Mean = tapply(Yield, Genotype, mean),
                         SD = tapply(Yield, Genotype, sd)))
##              Mean        SD
## COLOSSEO 4.893333 0.6798774
## CRESO    4.326667 0.4366158
## DUILIO   4.240000 0.1400000
## GRAZIA   4.340000 0.3764306
## IRIDE    4.963333 0.1892969
## SANCARLO 4.503333 0.2250185
## SIMETO   3.340000 0.3915354
## SOLEX    4.790000 0.2645751

La produzione di ogni unità sperimentale (parcella) è determinata da:

il genotipo in essa coltivato;
il blocco di cui fa parte;
altri effetti non conoscibile e puramente casuale (residuo).

Quindi, possiamo stimare un modello con due predittori nominali, come mostrato nell’Esempio 4.3 del Capitolo 4. Le analisi grafiche dei residui mostrano alcuni lievi segni di eteroschedasticità (Figura 10.1, sinistra), ma nessuna chiara evidenza di mancanza di normalità. La funzione leveneTest() non può essere utilizzata con dati provenienti da esperimenti a blocchi randomizzati, ma possiamo adattarla eseguendola sui residui in valore assoluto (Bhandary e Dai 2013; vedi riquadro sottostante); questo test non è significativo e il grafico di Box-Cox (non mostrato) conferma che non è necessaria alcuna trasformazione dei dati. Di conseguenza, concludiamo che non ci sono deviazioni significative dalle assunzioni di base e procediamo esaminando la tabella ANOVA. Il controllo preliminare dei gradi di libertà conferma che il modello è stato specificato correttamente (vale a dire, i DF sono uguali, rispettivamente, al numero di blocchi meno uno e al numero di genotipi meno uno) e, in base al P-value, rigettiamo l’ipotesi nulla concludendo che esistono differenze significative tra i genotipi.

# Example 10.1 [continuation]

# Model fitting with two nominal predictors
mod <- lm(Yield ~ Block + Genotype, data = dataset)

# Inspection of plots (not run)
# par(mfrow=c(2,2))
# plot(mod, which = 1)
# plot(mod, which = 2)
# boxcox(mod)

# Levene test (modified version for RCBDs)
leveneTest(abs(residuals(mod)) ~ Genotype, data = dataset)
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  7  0.7932 0.6037
##       16
# Variance partitioning
anova(mod)
## Analysis of Variance Table
## 
## Response: Yield
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## Block      2 0.7977 0.39883  3.8502 0.0465178 *  
## Genotype   7 5.6305 0.80436  7.7651 0.0006252 ***
## Residuals 14 1.4502 0.10359                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1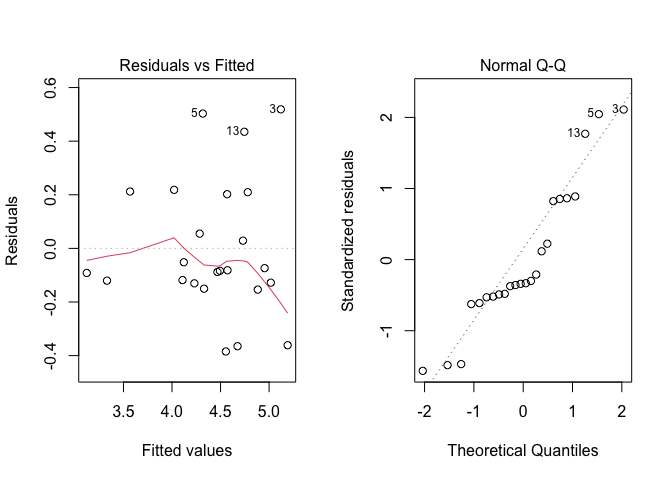

Figura 10.1: Analisi grafica dei residui per la prova di confronto varietale a blocchi randomizzati

Le stime dei parametri del modello sono relativamente poco interessanti in questo caso, mentre i confronti a coppie possono essere utili per la raccomandazione varietale. Con otto genotipi e, quindi, \((8 \times 7)/2 = 28\) contrasti, è necessaria una correzione per la molteplicità. Oltre ai confronti a coppie con i relativi intervalli di confidenza, riportiamo una tabella delle medie in ordine decrescente di resa, con le lettere di significanza. La conclusione è che Simeto è risultato significativamente peggiore di tutti gli altri genotipi, ad eccezione di Duilio.

# Example 10.1 [continuation]

# Multiple comparisons
meds <- emmeans(mod, ~Genotype)
confint(contrast(meds, method = "pairwise"))
##  contrast            estimate    SE df lower.CL upper.CL
##  COLOSSEO - CRESO      0.5667 0.263 14  -0.3606    1.494
##  COLOSSEO - DUILIO     0.6533 0.263 14  -0.2740    1.581
##  COLOSSEO - GRAZIA     0.5533 0.263 14  -0.3740    1.481
##  COLOSSEO - IRIDE     -0.0700 0.263 14  -0.9973    0.857
##  COLOSSEO - SANCARLO   0.3900 0.263 14  -0.5373    1.317
##  COLOSSEO - SIMETO     1.5533 0.263 14   0.6260    2.481
##  COLOSSEO - SOLEX      0.1033 0.263 14  -0.8240    1.031
##  CRESO - DUILIO        0.0867 0.263 14  -0.8406    1.014
##  CRESO - GRAZIA       -0.0133 0.263 14  -0.9406    0.914
##  CRESO - IRIDE        -0.6367 0.263 14  -1.5640    0.291
##  CRESO - SANCARLO     -0.1767 0.263 14  -1.1040    0.751
##  CRESO - SIMETO        0.9867 0.263 14   0.0594    1.914
##  CRESO - SOLEX        -0.4633 0.263 14  -1.3906    0.464
##  DUILIO - GRAZIA      -0.1000 0.263 14  -1.0273    0.827
##  DUILIO - IRIDE       -0.7233 0.263 14  -1.6506    0.204
##  DUILIO - SANCARLO    -0.2633 0.263 14  -1.1906    0.664
##  DUILIO - SIMETO       0.9000 0.263 14  -0.0273    1.827
##  DUILIO - SOLEX       -0.5500 0.263 14  -1.4773    0.377
##  GRAZIA - IRIDE       -0.6233 0.263 14  -1.5506    0.304
##  GRAZIA - SANCARLO    -0.1633 0.263 14  -1.0906    0.764
##  GRAZIA - SIMETO       1.0000 0.263 14   0.0727    1.927
##  GRAZIA - SOLEX       -0.4500 0.263 14  -1.3773    0.477
##  IRIDE - SANCARLO      0.4600 0.263 14  -0.4673    1.387
##  IRIDE - SIMETO        1.6233 0.263 14   0.6960    2.551
##  IRIDE - SOLEX         0.1733 0.263 14  -0.7540    1.101
##  SANCARLO - SIMETO     1.1633 0.263 14   0.2360    2.091
##  SANCARLO - SOLEX     -0.2867 0.263 14  -1.2140    0.641
##  SIMETO - SOLEX       -1.4500 0.263 14  -2.3773   -0.523
## 
## Results are averaged over the levels of: Block 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 8 estimates
# Letter display
cld(meds, Letters = LETTERS, reverse = T)
##  Genotype emmean    SE df lower.CL upper.CL .group
##  IRIDE      4.96 0.186 14     4.56     5.36  A    
##  COLOSSEO   4.89 0.186 14     4.49     5.29  A    
##  SOLEX      4.79 0.186 14     4.39     5.19  A    
##  SANCARLO   4.50 0.186 14     4.10     4.90  A    
##  GRAZIA     4.34 0.186 14     3.94     4.74  A    
##  CRESO      4.33 0.186 14     3.93     4.73  A    
##  DUILIO     4.24 0.186 14     3.84     4.64  AB   
##  SIMETO     3.34 0.186 14     2.94     3.74   B   
## 
## Results are averaged over the levels of: Block 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 8 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

10.2 Esempio 10.2: confronto tra co-adiuvanti in un esperimento a quadrato latino

Consideriamo un esperimento a quadrato latino con quattro repliche, finalizzato a confrontare tre possibili co-adiuvanti per l’erbicida rimsulfuron (Onofri, 1990; dati non pubblicati). I risultati di questo esperimento sono disponibili nel dataset ‘adjuvantsLS’, nel package statforbiology; la colonna ‘Yield’ è la risposta, la colonna ‘Adjuvant’ il predittore nominale, mentre le colonne ‘Row’ and ‘Column’ rappresentano le righe e le colonne della griglia a quadrato latino e costituiscono i due fattori di raggruppamento da inserire nel modello. Le tre variabili indipendenti dovranno essere trasformate in fattori prima dell’analisi, sebbene ciò sia strettamente necessario solo per le righe e le colonne, che sono caratterizzate da codifica numerica. Invece di trasformare le tre variabili una alla volta (come nell’esempio 10.1), possiamo utilizzare la funzione transform(), passandole il ‘dataframe’ come primo argomento e l’elenco delle trasformazioni da eseguire all’interno di tale ‘dataframe’ (vedere il codice più sotto).

L’EDA si basa sull’analisi delle medie aritmetiche e delle deviazioni standard (DS) dei diversi trattamenti: la media per il tensioattivo sembra essere più alta rispetto alle altre medie. Allo stesso tempo, non ci sono evidenti differenze tra i co-adiuvanti in termini di deviazioni standard.

# Example 10.2
# Comparing adjuvants on a latin square

# Loading the packages
library(statforbiology)
library(MASS)
library(emmeans)
library(multcomp)

# Loading and transforming the data
dataset <- getAgroData("adjuvantsLS")
dataset <- transform(dataset, 
                     Adjuvant = factor(Adjuvant),
                     Row = factor(Row),
                     Column = factor(Column))
head(dataset[,c(2, 6, 7, 24)])
##           Adjuvant Column Row Yield
## 1 AmmoniumSulphate      1   3 58.23
## 2 AmmoniumSulphate      2   1 47.98
## 3 AmmoniumSulphate      3   4 92.39
## 4 AmmoniumSulphate      4   2 85.97
## 5       MineralOil      1   2 73.99
## 6       MineralOil      2   4 92.97
# EDA
with(dataset, data.frame(Mean = tapply(Yield, Adjuvant, mean),
                         SD = tapply(Yield, Adjuvant, sd)))
##                      Mean       SD
## AmmoniumSulphate  71.1425 21.40518
## MineralOil       101.1475 23.00979
## None              80.5525 30.51889
## Surfactant       115.4250 20.69268

In questo esempio, abbiamo un trattamento sperimentale e due effetti ‘blocco’ che debbono necessariamente essere inclusi nel modello (Jensen et al., 2018). Di conseguenza, il modello causa-effetto può essere così definito:

\[Y_{ijk} = \mu + \gamma_k + \beta_j + \alpha_i + \varepsilon_{ijk}\]

dove \(\mu\) è l’intercetta, \(\gamma\) è l’effetto della k-esima riga, \(\beta\) è l’effetto della j-esima colonna e \(\alpha\) è l’effetto dell’i-esimo coadiuvante. L’elemento \(\varepsilon_{ijk}\) rappresenta la componente random individuale, di ogni osservazione e si assume normalmente distribuita, con media 0 e deviazione standard \(\sigma\).

Dopo il ‘fitting’, estraiamo i residui e li sottoponiamo ad analisi grafica, che non rivela problemi di alcun tipo (Figura 10.2), mentre il grafico di Box-Cox conferma che non è necessaria alcuna trasformazione (non mostrato). Pertanto, possiamo procedere all’ANOVA per testare la significatività di tutti i fattori sperimentali.

# Example 10.2 [continuation]

# Fitting the model
mod <- lm(Yield ~ Adjuvant + Row + Column, data = dataset)

# checking the residuals (not run here)
# plot(mod, which = 1)
# plot(mod, which = 2)
# boxcox(mod)

# Variance partitioning
anova(mod)
## Analysis of Variance Table
## 
## Response: Yield
##           Df Sum Sq Mean Sq F value   Pr(>F)   
## Adjuvant   3 4793.9 1597.96 14.9051 0.003458 **
## Row        3  375.8  125.28  1.1685 0.396678   
## Column     3 6022.6 2007.53 18.7253 0.001893 **
## Residuals  6  643.3  107.21                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Figura 10.2: Analisi grafica dei residui per la prova di confronto tra metodi costruttivi

La differenza tra i co-adiuvanti è significativa (valore P = 0,0035) e la procedura di confronto multiplo rivela che il tensioattivo ha migliorato significativamente le prestazioni dell’erbicida, rispetto a quando è stato utilizzato da solo, mentre la resa con olio minerale non è stata significativamente inferiore a quella ottenuta col tensioattivo.

# Example 10.2 [continuation]

# Multiple comparisons
avgs <- emmeans(mod, ~Adjuvant)
confint(contrast(avgs, method = "pairwise"))
##  contrast                      estimate   SE df lower.CL upper.CL
##  AmmoniumSulphate - MineralOil   -30.00 7.32  6   -55.35    -4.66
##  AmmoniumSulphate - None          -9.41 7.32  6   -34.75    15.93
##  AmmoniumSulphate - Surfactant   -44.28 7.32  6   -69.63   -18.94
##  MineralOil - None                20.59 7.32  6    -4.75    45.94
##  MineralOil - Surfactant         -14.28 7.32  6   -39.62    11.07
##  None - Surfactant               -34.87 7.32  6   -60.22    -9.53
## 
## Results are averaged over the levels of: Row, Column 
## Confidence level used: 0.95 
## Conf-level adjustment: tukey method for comparing a family of 4 estimates
cld(avgs, Letters = LETTERS, reversed = TRUE)
##  Adjuvant         emmean   SE df lower.CL upper.CL .group
##  Surfactant        115.4 5.18  6    102.8    128.1  A    
##  MineralOil        101.1 5.18  6     88.5    113.8  AB   
##  None               80.6 5.18  6     67.9     93.2   BC  
##  AmmoniumSulphate   71.1 5.18  6     58.5     83.8    C  
## 
## Results are averaged over the levels of: Row, Column 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 4 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

10.3 Esempio 10.3: interazione tra genotipo e concimazione azotata

Quindici genotipi di frumento sono stati confrontati a due diversi livelli di fertilizzazione azotata, utilizzando un disegno a blocchi randomizzati con tre repliche. L’esperimento mirava a valutare se la raccomandazione varietale cambiasse al cambiare del livello di concimazione azotata. Il set di dati è stato generato tramite simulazione Monte Carlo, a partire dai risultati riportati in (Stagnari et al., 2003) ed è disponibile come ‘NGenotypeFull’ nel package statforbiology.

In questo esperimento, la resa è determinata da quattro effetti:

blocco
genotipo
livello di azoto
interazione tra genotipo e livello di azoto

Di conseguenza, il modello mostrato può essere codificato come nell’Esempio 4.4 (Capitolo 4), aggiungendo l’effetto blocco. Per stimare questo modello, possiamo caricare i dati e trasformare i predittori numerici in fattori. Per questa trasformazione, nel riquadro sottostante abbiamo utilizzato la funzione lapply() invece della funzione transform(), che avevamo utilizzato in un esempio precedente. Con lapply(), le variabili da trasformare vengono recuperate utilizzando gli indici di colonna, vengono trasformate utilizzando la funzione factor() (passata come secondo argomento) e riassegnate alle stesse posizioni che avevano in precedenza nel ‘dataframe’.

Per brevità, saltiamo l’EDA e passiamo direttamente alla stima del modello; L’analisi grafica dei residui produce i risultati mostrati nella Figura \(\ref{fig:figName133}\), dove non osserviamo deviazioni evidenti rispetto agli assunti di base per i modelli lineari; pertanto, procediamo con l’ANOVA.

# Example 10.3
# Genotype by Nitrogen Interactions

# Loading the packages
library(statforbiology)
library(MASS)
library(car)
library(emmeans)
library(multcomp)

# Loading and transforming the data
dataset <- getAgroData("NGenotypeFull")
dataset[,1:3] <- lapply(dataset[,1:3], factor)
head(dataset)
##   Block Genotype N Yield
## 1     1        A 1 2.146
## 2     2        A 1 2.433
## 3     3        A 1 2.579
## 4     1        A 2 2.362
## 5     2        A 2 2.919
## 6     3        A 2 2.912
# Model fitting
mod <- lm(Yield ~ Block + Genotype * N, data=dataset)

# Model checking (not run)
# plot(mod, which = 1)
# plot(mod, which = 2)
# boxcox(mod)

# Variance partitioning
anova(mod)
## Analysis of Variance Table
## 
## Response: Yield
##            Df  Sum Sq Mean Sq F value    Pr(>F)    
## Block       2  0.0944 0.04721  1.3310 0.2721536    
## Genotype   14 10.5408 0.75291 21.2297 < 2.2e-16 ***
## N           1  1.6246 1.62463 45.8092 7.175e-09 ***
## Genotype:N 14  1.6061 0.11472  3.2349 0.0008204 ***
## Residuals  58  2.0570 0.03547                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1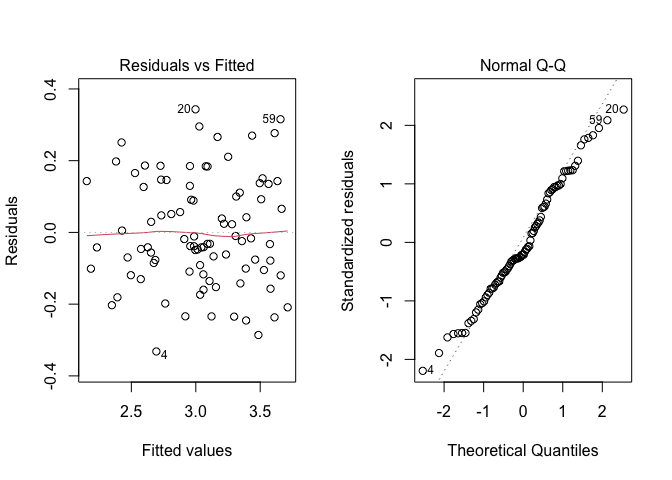

Figura 10.3: Analisi grafiche dei residui per l’esperimento fattoriale di confronto tra genotipi a due dosi di azoto (Esempio 10.3).

La lettura della tabella ANOVA per un esperimento a due vie richiede una certa attenzione ed è fondamentale procedere dal basso verso l’alto, considerando che un’interazione cross-over significativa potrebbe nascondere gli effetti dei fattori principali (vedere Capitolo 4). In generale, ogniqualvolta l’interazione sia significativa, dovremmo sempre riportare e commentare le medie delle combinazioni tra i livelli dei fattori sperimentali. D’altra parte, se l’interazione non fosse significativa, potremmo invece riassumere i risultati riportando e commentando solo le medie degli effetti principali.

In questo esempio, l’interazione è significativa e la conclusione è che la raccomandazione varietale non può essere univoca, ma deve cambiare a seconda del livello di fertilizzazione azotata. Pertanto, è necessario riportare e separatamente le medie dei genotipi per ciascun livello di azoto; in questa situazione i confronti a coppie tra genotipi potrebbero essere effettuati in due modi:

confrontando tutti i genotipi, anche se concimati in modo diverso;
confrontando tra loro solo i genotipi concimati nello stesso modo.

Il primo approccio è molto flessibile, ma implica un numero elevato di contrasti \((10 x 9) / 2 = 45\) contrasti); di conseguenza, implica anche un forte aggiustamento per la molteplicità, quindi una potenza ridotta e maggiori rischi di errori di II specie. Tale approccio è da raccomandare solo se strettamente necessario e, in questo caso, la codifica R per la funzione emmeans() deve utilizzare l’operatore : (ad esempio: emmeans(mod, ~Genotype:N)).

Il secondo approccio implica invece un numero inferiore di confronti (\(2 x [5 x 4)/2 = 20\) confronti] e, in questo caso, appare più logico e sensato, da un punto di vista agronomico. Nel riquadro sottostante questo approccio viene implementato utilizzando l’operatore di ‘condizionamento’ (|).

# Example 10.3 [continuation]

# Pairwise comparisons within Nitrogen levels
GNmeans2 <- emmeans(mod, ~Genotype|N)
cld(GNmeans2, Letters=LETTERS)
## N = 1:
##  Genotype emmean    SE df lower.CL upper.CL .group  
##  A          2.39 0.109 58     2.17     2.60  A      
##  M          2.43 0.109 58     2.21     2.65  AB     
##  C          2.53 0.109 58     2.32     2.75  ABC    
##  G          2.61 0.109 58     2.39     2.83  ABCD   
##  H          2.69 0.109 58     2.47     2.91  ABCD   
##  I          2.77 0.109 58     2.55     2.99  ABCDE  
##  B          2.92 0.109 58     2.70     3.13  ABCDEF 
##  D          2.96 0.109 58     2.74     3.17   BCDEF 
##  N          2.99 0.109 58     2.77     3.21    CDEFG
##  O          3.00 0.109 58     2.78     3.22    CDEFG
##  F          3.06 0.109 58     2.85     3.28    CDEFG
##  J          3.10 0.109 58     2.88     3.31     DEFG
##  E          3.26 0.109 58     3.04     3.47      EFG
##  K          3.40 0.109 58     3.18     3.61       FG
##  L          3.52 0.109 58     3.31     3.74        G
## 
## N = 2:
##  Genotype emmean    SE df lower.CL upper.CL .group  
##  C          2.19 0.109 58     1.97     2.41  A      
##  I          2.63 0.109 58     2.41     2.85  AB     
##  A          2.73 0.109 58     2.51     2.95  ABC    
##  M          2.99 0.109 58     2.77     3.21   BCD   
##  H          3.02 0.109 58     2.80     3.24   BCD   
##  F          3.11 0.109 58     2.90     3.33   BCDE  
##  G          3.13 0.109 58     2.91     3.34   BCDEF 
##  B          3.24 0.109 58     3.02     3.46    CDEF 
##  D          3.35 0.109 58     3.13     3.56     DEF 
##  O          3.35 0.109 58     3.13     3.57     DEF 
##  E          3.47 0.109 58     3.25     3.68     DEF 
##  L          3.53 0.109 58     3.32     3.75     DEF 
##  J          3.62 0.109 58     3.40     3.83      EF 
##  K          3.62 0.109 58     3.40     3.83      EF 
##  N          3.67 0.109 58     3.45     3.89       F 
## 
## Results are averaged over the levels of: Block 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 15 estimates 
## significance level used: alpha = 0.05 
## NOTE: If two or more means share the same grouping symbol,
##       then we cannot show them to be different.
##       But we also did not show them to be the same.

10.4 Esempio 10.4: confronto tra incroci in un disegno fattoriale gerarchico

L’esempio precedente era relativo ad un disegno fattoriale completamente incrociato, dato che i livelli delle lavorazioni erano gli stessi per ogni livello di diserbo. In alcuni casi possiamo trovare disegni innestati, dove i livelli di un fattore cambiano al cambiare dei livelli dell’altro fattore. Nell’esempio seguente abbiamo considerato tre linee pure impollinanti di mais (A1, A2 ed A3), che abbiamo incrociato con tre linee pure portaseme, diverse per ogni impollinante (B1, B2, B3 per A1, B4, B5, B6 per A2 e B7, B8, B9 per A3). Alla fine abbiamo nove ibridi in tre gruppi, a seconda della linea impollinante. L’esperimento è stato disegnato in blocchi randomizzati completi con 4 repliche (36 osservazioni in totale) e i risultati sono disponibili come ‘crosses’ nel package statforbiology.

In questo esperimento, la produzione del mais dipende dal blocco e dall’effetto paterno, mentre l’effetto materno può essere solo determinato entro ogni linea impollinante. Si dice che l’effetto materno è innestato entro l’effetto paterno, come mostrato in Figura 10.4. Pertanto, il modello lineare risulta così definito:

\[Y_{ijk} = \mu + \gamma_k + \alpha_i + \delta_{ij} + \varepsilon_{ijk}\]

dove \(\gamma_k\) è l’effetto del blocco \(k\), \(\alpha_i\) è l’effetto dell’impollinante \(i\) e \(\delta_{ij}\) è l’effetto del portaseme \(j\) entro ogni linea impollinante \(i\). La componente random \(\varepsilon\) viene assunta, come al solito, gaussiana e omoscedastica, con media 0 e deviazione standard uguale a \(\sigma\).

La differenza con un modello ANOVA completamente incrociato dovrebbe essere chiara: in quest’ultimo caso abbiamo due effetti, A, B e la loro interazione A:B, mentre in un modello innestato abbiamo solo l’effetto A e l’effetto B entro A, mentre l’effetto principale B manca, in quanto non esiste in pratica.

Figura 10.4: Struttura di un disegno sperimentale gerarchico

In R, questo modello gerarchico può essere codificato utilizzando l’operatore di nesting /, come mostrato nel riquadro sottostante. Le analisi grafiche dei residui consentono di escludere qualsiasi deviazione significativa rispetto agli assunti di base (non mostrate) e la tabella ANOVA mostra che tutti gli effetti sono significativi e, pertanto, possiamo esaminare e confrontare le medie dei diversi ibridi, anche considerando che l’effetto paterno è relativamente poco importante, dato che le linee impollinanti sono incrociate con linee portaseme diverse. Il confronto multiplo viene lasciato al lettore come esercizio.

# Example 10.4
# Comparing crosses in a nested factorial design

# Loading the packages
library(statforbiology)
library(MASS)

# Loading the data and fitting a model with a nested effect
dataset <- getAgroData("crosses")
dataset[,1:3] <- lapply(dataset[,1:3], factor)
head(dataset, 5)
##   Male Female Block     Yield
## 1   A1     B1     1  9.984718
## 2   A1     B1     2 13.932663
## 3   A1     B1     3 12.201312
## 4   A1     B1     4  1.916661
## 5   A1     B2     1  8.928465
# Model fitting and parameter estimation
mod <- lm(Yield ~ Block + Male/Female, data = dataset)

# Analyses of residuals (not shown)
# plot(mod, which = 1)
# plot(mod, which = 2)
# boxcox(mod)

# Variance partitioning
anova(mod)
## Analysis of Variance Table
## 
## Response: Yield
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## Block        3 383.75 127.917  44.355 6.051e-10 ***
## Male         2 134.76  67.378  23.363 2.331e-06 ***
## Male:Female  6 575.16  95.860  33.239 1.742e-10 ***
## Residuals   24  69.21   2.884                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In conclusione, vediamo che l’analisi dei disegni con due fattori innestati è piuttosto simile a quella per due fattori incrociati, con l’unica eccezione che l’effetto principale per il fattore innestato non è incluso nel modello.

10.5 Esempio 10.5: un esperimento di germinazione ripetuto due volte

Nonostante possano essere molto precisi e significativi, i risultati di un singolo esperimento in agricoltura sono solitamente considerati abbastanza deboli, se non sono confermati in altri esperimenti simili. Infatti, un singolo esperimento può essere influenzato da ‘disturbi’ di ogni tipo, errori di misurazione, eventi imprevisti o intrusioni; inoltre, un risultato anche significativo può essere valido solo nelle condizioni in cui è stato osservato, senza essere necessariamente riproducibile in altre condizioni (vedi Capitolo 1).

Per queste ragioni, in agricoltura siamo soliti ripetere gli esperimenti in più anni e/o in più località, oppure, nel caso di esperimenti in condizioni controllate, con materiale vegetale diverso. Quando gli esperimenti vengono ripetuti, oltre ad analizzare i dati di ciascun esperimento separatamente, è molto utile tentare un’analisi finale aggregata, per saggiare l’ipotesi che le prove sperimentali non differiscano significativamente l’una dall’altra.

Consideriamo un esperimento per confrontare la germinazione di tre genotipi di colza (Pace et al., 2012), organizzato in cella climatica, secondo uno schema a blocchi randomizzati con sei repliche. Le unità sperimentali erano piastre Petri da 50 semi ciascuna e i blocchi erano i diversi scaffali (variabile ‘shelf’) di una cella climatica, mantenuta a 20°C per l’intera durata dell’esperimento. Per confermare i risultati, l’esperimento è stato ripetuto indipendentemente in un altro forno alla stessa temperatura (variabile ‘run’); in entrambi gli esperimenti, dopo 15 giorni dall’inizio, è stato contato il numero di semi germinati ed i conteggi sono stati espressi come proporzione rispetto al numero di semi posti a germinare (Final Germinated Proportion; FGP).

I risultati di questi due esperimenti sono disponibili nel dataset ‘FGP_rape’, contenuto nel package statforbiology; dopo aver caricato i dati, è necessario trasformare i predittori numerici (‘run’ e ‘shelf’) in fattori (vedi il codice più sotto). In questa situazione, l’EDA dovrebbe includere le analisi separate per ogni esperimento, al fine di garantire che non vi siano outliers o violazioni degli assunti di base in nessuno degli esperimenti. Inoltre, è necessario assicurarsi che le varianze dei residui dei diversi esperimenti siano simili (omoschedasticità tra esperimenti).

Per effettuare le analisi separate, è possibile semplificare il codice utilizzando la strategia split-apply-combine (Wickham, 2011), basata sulle funzioni by() e lapply(). La prima opera sui sottoinsiemi del dataset selezionato, suddivisi in base a una variabile di classificazione (in questo caso la variabile run) e produce una lista con i risultati della funzione lm() applicata a ciascun sottoinsieme. Questa lista può essere analizzata con la funzione lapply(), che permette di applicare le funzioni leveneTest() e shapiro.test() a ciascun elemento della lista. Possiamo vedere che nessuno dei due test indica significative deviazioni rispetto agli assunti di base.

Per verificare l’omoschedasticità tra esperimenti, si può utilizzare il test F max di Hartely (Hartley, 1950), che consiste nel calcolare il rapporto tra la varianza residua massima e minima tra quelle osservate, che, in questo caso però, sono solo due. La significatività del test può essere ottenuta grazie alla distribuzione pmaxFratio(), che è contenuta nel package SuppDists (Wheeler, 2024). In questo caso, il P-value non è sufficientemente basso per il rifiuto dell’ipotesi nulla, il che conferma l’omoschedasticità tra esperimenti. Le analisi sono riportate nel riquadro sottostante

# Example 10.5
# A germination experiment in two runs

# Loading packages
library(statforbiology)
library(car)
library(SuppDists)
library(MASS)
library(emmeans)
library(multcomp)

# Loading and transforming the data
dataset <- getAgroData("FGP_rape")
dataset[,1:5] <- lapply(dataset[,1:5], factor)
head(dataset)
##   Dish Run Shelf     Species Genotype  FGP
## 1    1   1     1 OilseedRape        A 0.81
## 2   13   1     1 OilseedRape        B 0.81
## 3   25   1     1 OilseedRape        C 0.74
## 4    2   1     2 OilseedRape        A 0.91
## 5   14   1     2 OilseedRape        B 0.92
## 6   26   1     2 OilseedRape        C 0.76
# Fitting linear models to the two runs, separately
lmFits <- by(dataset, dataset$Run,  
      function(df) lm(FGP ~ Genotype + Shelf, data = df) )

# Check for within-experiments homoscedasticity
# Modified Levene's test for RCBDs (see Code box 10.2)
levTest <- by(dataset, dataset$Run,  
      function(df) 
        leveneTest(abs(residuals(lm(FGP ~ Genotype + Shelf, data = df))),
                        df$Genotype))
levTest
## dataset$Run: 1
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  0.2779 0.7612
##       15               
## ---------------------------------------------------- 
## dataset$Run: 2
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  1.5841 0.2376
##       15
lapply(lmFits, function(mods) shapiro.test(residuals(mods)))
## $`1`
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mods)
## W = 0.90201, p-value = 0.06229
## 
## 
## $`2`
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mods)
## W = 0.93221, p-value = 0.2124
# Check for homoscedasticity of errors across runs
# by the Hartley Fmax test
mses <- unlist(
  lapply(lmFits, function(mods) summary(mods)$sigma^2))
Fmax <- max(mses)/min(mses)
pmaxFratio(Fmax, 15, 2, lower.tail = FALSE)
## [1] 0.7404869
# Variance partitioning
lapply(lmFits, function(mods) anova(mods))
## $`1`
## Analysis of Variance Table
## 
## Response: FGP
##           Df   Sum Sq   Mean Sq F value   Pr(>F)    
## Genotype   2 0.033011 0.0165056 15.6864 0.000825 ***
## Shelf      5 0.019911 0.0039822  3.7846 0.034871 *  
## Residuals 10 0.010522 0.0010522                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## $`2`
## Analysis of Variance Table
## 
## Response: FGP
##           Df   Sum Sq   Mean Sq F value    Pr(>F)    
## Genotype   2 0.042544 0.0212722 16.9876 0.0006081 ***
## Shelf      5 0.001761 0.0003522  0.2813 0.9129498    
## Residuals 10 0.012522 0.0012522                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

L’EDA dimostra che non ci sono problemi con le assunzioni di base e che l’effetto del trattamento è stato significativo in entrambi gli esperimenti. Passando alle analisi del dataset aggregato, possiamo notare che esso è totalmente simile a quello derivante da un qualunque esperimento fattoriale a due vie, con l’unica differenza che l’effetto blocco non è incrociato, ma ‘innestato’ all’interno degli esperimento, poiché i ripiani sono diversi nei diversi esperimenti, che sono stati eseguiti in celle climatiche diverse. Di conseguenza, il modello finale è:

\[y_{ijk} = \mu + \gamma_{ik} + \alpha_i + \beta_j + \alpha\beta_{ij} + \varepsilon_{ijk}\]

dove \(y\) è la risposta per l’i-esimo esperimento, il j-esimo genotipo e il k-esimo scaffale, \(\mu\) è l’intercetta, \(\gamma_{ik}\) è l’effetto del k-esimo scaffale nell’i-esimo esperimento, \(\alpha_i\) è l’effetto dell’i-esimo esperimento, \(\beta_j\) è l’effetto del j-esimo genotipo, \(\alpha\beta_{ij}\) è l’interazione ‘genotipo per esperimento’, mentre \(\varepsilon_{ijk}\) è il residuo per ciascuna osservazione, che si presume distribuito normalmente e omoschedastico (\(\epsilon_{ijk} \sim N(0, \sigma_{\varepsilon})\)).

# Example 10.5 [continuation]

# Pooled analyses: model fitting
mod <- lm(FGP ~ Genotype * Run + Run:Shelf, data = dataset)

# model checking (not shown)
# plot(mod, which = 1)
# plot(mod, which = 2)
# boxcox(mod)

# Variance partitioning
anova(mod)
## Analysis of Variance Table
## 
## Response: FGP
##              Df   Sum Sq  Mean Sq F value    Pr(>F)    
## Genotype      2 0.074289 0.037144 32.2372 5.534e-07 ***
## Run           1 0.003025 0.003025  2.6254    0.1208    
## Genotype:Run  2 0.001267 0.000633  0.5497    0.5856    
## Run:Shelf    10 0.021672 0.002167  1.8809    0.1100    
## Residuals    20 0.023044 0.001152                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

L’analisi della tabella ANOVA per un insieme di esperimenti ripetuti fornisce un’idea della riproducibilità dei risultati. È possibile riscontrare le seguenti situazioni:

L’interazione “esperimento per trattamento” è significativa. In questo caso, dovremmo concludere che gli effetti dei trattamenti e, probabilmente, la loro graduatoria, sono cambiati nei diversi esperimenti. Di conseguenza, l’aggregazione dei risultati non è possibile e dovremmo visualizzare e confrontare solo le medie dei trattamenti all’interno di ciascun esperimento.
L’interazione non è significativa, ma l’effetto principale del trattamento lo è. Dovremmo quindi concludere che gli effetti dei trattamenti e degli esperimenti sono stati indipendenti e additivi; di conseguenza, le medie dei trattamenti sono cambiate nei diversi esperimenti, ma la loro graduatoria (e quindi il giudizio di merito) è risultato pienamente riproducibile. Spetta al ricercatore decidere se sia appropriato calcolare e visualizzare le medie generali dei trattamenti o mantenerle separate per i diversi esperimenti.
Né l’interazione né gli effetti principali sono significativi. La conclusione è che i risultati degli esperimenti ripetuti sono pienamente riproducibili e di solito è sufficiente riportare solo le medie generali dei trattamenti.

Nel nostro esempio, osserviamo che è significativo solo l’effetto del genotipo, il che significa che i risultati sono stati pienamente riproducibili. Pertanto, calcoliamo le medie generali dei genotipi e le sottoponiamo a confronto multiplo.

# Example 10.5 [continuation]

# Multiple comparisons for pooled data

cld(emmeans(mod, ~ Genotype), Letters = LETTERS)
## Genotype  emmean     SE df  lower.CL upper.CL .group
##  C         0.781 0.0098 20    0.760    0.801  A    
##  A         0.871 0.0098 20    0.850    0.891   B   
##  B         0.882 0.0098 20    0.862    0.903   B

Prima di concludere, è necessario sottolineare che il metodo di analisi dei dati proposto per questo esempio è sempre appropriato, sebbene in alcuni casi, soprattutto quando il numero di esperimenti è molto elevato, potrebbe essere opportuno impiegare un altro metodo, di cui verrà fornito un esempio nel Capitolo 12.

10.6 Altre letture

Belocchi A, Fornara M, Ciriciofolo E, Biancolatte V, Gosparini E, Piccioni C, Desiderio E (2003) Grano duro: Risultati 2002–03 della Rete Nazionale. Lazio e Umbria. L’Informatore Agrario 19(Suppl.1):41–44
Bhandary M, Dai H (2013) An alternative test for the equality of variances for several populations in randomised complete block design. Stat Methodol 11:22–35. https://doi.org/10.1016/j. stamet.2012.08.002. https://linkinghub.elsevier.com/retrieve/pii/S1572312712000482
Hartley HO (1950) The Maximum F-ratio as a short-cut test for heterogeneity of vari- ance. Biometrika 37(3/4):308. https://doi.org/10.2307/2332383. https://www.jstor.org/stable/ 2332383?origin=crossref
Jensen SM, Schaarschmidt F, Onofri A, Ritz C (2018) Experimental design matters for statistical analysis: how to handle blocking: experimental design matters for statistical analysis. Pest Manag Sci 74(3):523–534. https://doi.org/10.1002/ps.4773. http://doi.wiley.com/10.1002/ps. 4773
Kuehl RO (2000) Design of Experiments: Statistical Principles of Research Design and Analysis. Duxbury Press, Pacific Grove
Le Clerg EL, Leonard WH, Clark AG (1962) Field Plot Technique. Burgess Publishing Company, Minneapolis
Onofri A, Tei F (1994) Influence of application timing on the effectiveness of rimsulfuron against rhizome Sorghum halepense (L.) Pers. In: Tei F, Onofri A (eds) Weed Control in Sustainable Agriculture in the Mediterranean Area. Proceedings 5th EWRS Mediterranean Symposium, Università degli Studi di Perugia, Reprints, pp 105–111
Pace R, Benincasa P, Ghanem ME, Quinet M, Lutts S (2012) Germination of untreated and primed seeds in rapeseed (brassica napus var oleifera del.) under salinity and low matric potential. Exp Agricul 48(02):238–251. https://doi.org/10.1017/S0014479711001189. http:// www.journals.cambridge.org/abstract_S0014479711001189
Stagnari F, Onofri A, Codianni P, Pisante M (2013) Durum wheat varieties in N-deficient environments and organic farming: a comparison of yield, quality and stability performances. Plant Breed 132:266–275
Wheeler B (2024) SuppDists: Supplementary Distributions. https://CRAN.R-project.org/package= SuppDists, r package version 1.1-9.8
White JW, Boote KJ, Kimball BA, Porter C, Salmeron M, Shelia V, Thorp KR, Hoogenboom G (2025) From field to analysis: strengthening reproducibility and confirmation in research for sustainable agriculture. npj Sustain Agricul 3(1):27. https://doi.org/10.1038/s44264-025- 00067-z. https://www.nature.com/articles/s44264-025-00067-z
Wickham H (2011) The split-apply-combine strategy for data analysis. J Stat Softw 40(1):1–29. https://doi.org/10.18637/jss.v040.i01. http://www.jstatsoft.org/v40/i01/

10.7 Esercizi

Per tutti gli esercizi che seguono, utilizzate il piano di lavoro proposto all’inizio di questo capitolo e cercate di giungere a conclusioni attendibili. Tutti i dataset sono disponibili nel package statforbiology e sono accessibili tramite la funzione getAgroData(). Il nome del dataset è specificato per ogni esercizio.

È stato condotto un esperimento con un disegno completamente randomizzato per confrontare la resa di 5 genotipi di grano. I risultati (in bushel per acro) sono riportati nella tabella seguente: determinare il genotipo migliore e trarre conclusioni attendibili. L’esempio è tratto da Le Clerg (1962) e il dataset è disponibile come “LeClerg”.

Variety 1 2 3

A 32.4 34.3 37.3

B 20.2 27.5 25.9

C 29.2 27.8 30.2

D 12.8 12.3 14.8

E 21.7 24.5 23.4
Colture cellulari di pomodoro sono state allevate su tre tipi di substrato, ottenuti aggiungendo al testimone una certa quantità di glucosio, fruttosio o saccarosio. L’esperimento è stato condotto con un disegno completamente randomizzato con 5 repliche, osservando la crescita delle cellule su ogni unità sperimentale. Determinare quale substrato ha prodotto la crescita cellulare più elevata e commentare i risultati. Il dataset è mostrato nella tabella sottostante ed è disponibile come “sugarsMedia”.

Control Glucose Fructose Sucrose

5.285 4.020 3.705 4.776

5.737 3.648 3.714 3.771

5.320 3.861 3.110 4.742

6.050 4.098 3.522 4.246

5.705 3.919 3.957 4.212
È stata valutata la durata di un impianto di riscaldamento (in ore prima del guasto), a seconda della temperatura di esercizio. L’esperimento è stato organizzato includendo quattro diverse temperature ed è stato disegnato con randomizzazione completa e 6 repliche. Considerare la temperatura come un fattore e determinare la temperatura di esercizio ottimale per massimizzare la durata dell’impianto. I risultati sono mostrati di seguito e sono disponibili come ‘failureTimes’. SUGGERIMENTO: in questo esercizio è necessaria una trasformazione stabilizzante, che non viene riconosciuta automaticamente dalla funzione emmeans(). Pertanto, la retro-trasformazione richiederà il processo descritto alla fine della Sezione 9.6.

Temp 1 2 3 4 5 6

1520 1953 2135 2471 4727 6134 6314

1620 1190 1286 1550 2125 2557 2845

1660 651 837 848 1038 1361 1543

1708 511 651 651 652 688 729

Variety	1	2	3
A	32.4	34.3	37.3
B	20.2	27.5	25.9
C	29.2	27.8	30.2
D	12.8	12.3	14.8
E	21.7	24.5	23.4

Control	Glucose	Fructose	Sucrose
5.285	4.020	3.705	4.776
5.737	3.648	3.714	3.771
5.320	3.861	3.110	4.742
6.050	4.098	3.522	4.246
5.705	3.919	3.957	4.212

Temp	1	2	3	4	5	6
1520	1953	2135	2471	4727	6134	6314
1620	1190	1286	1550	2125	2557	2845
1660	651	837	848	1038	1361	1543
1708	511	651	651	652	688	729

Un entomologo ha contato il numero di uova deposte da un lepidottero su tre substrati diversi, in un esperimento a randomizzazione completa 15 repliche. Identificare il substrato con la più bassa ovideposizione. I risultati sono riportati di seguito e sono disponibili come ‘lepidopteraEggs’.

Rep	A	B	C
1	456	118	72
2	411	213	99
3	594	74	24
4	280	26	20
5	664	163	89
6	379	76	47
7	444	240	32
8	436	75	29
9	294	108	1
10	431	68	33
11	476	108	20
12	382	153	22
13	413	98	27
14	485	120	39
15	440	126	12

È stato condotto un esperimento in un aranceto nel Sud Italia, comprendente 5 sistemi di irrigazione in 5 blocchi completi. Le rese osservate (in tonnellate per ettaro) sono riportate nella tabella sottostante e sono disponibili come ‘orangeIrrigation’. Qual è il sistema di irrigazione che ha offerto le migliori prestazioni?

Method	1	2	3	4	5
Localised	26.7	27.9	51.2	29.0	34.8
Surface	46.4	47.7	33.9	32.7	21.7
Sprinkler	38.5	29.1	33.6	11.8	27.6
Sprinker+localised	41.3	33.9	31.3	5.8	12.1
Submersion	35.2	46.9	19.8	27.9	26.7

È stata condotta una prova di fertilizzazione, con cinque trattamenti e un disegno a blocchi randomizzati con cinque repliche. Per circostanze casuali impreviste, è venuto a mancare un dato per il trattamento “50N” nel secondo blocco. I dati osservati sono i contenuti percentuali di P₂O₅ nei campioni di foglie raccolte in ogni parcella e sono disponibili come ‘missingVal’. Analizzando i dati rispondete alle seguenti domande. È conveniente fertilizzare? È conveniente arrivare a 100 kg/ha con fertilizzazione azotata? L’aggiunta di P₂O₅ è una pratica conveniente? SUGGERIMENTO: considerare il valore mancante e assicurarsi che l’approccio utilizzato per l’ANOVA sia corretto

Fert 1 2 3 4 5

100N 6.9 9.6 5.6 7.4 8.2

100N+75P 9.6 9.3 12.0 10.6 11.6

50N 7.3 NA 7.7 7.7 7.0

50N+75P 10.8 9.2 8.8 9.9 9.4

Unfertilised 5.6 6.1 5.3 5.9 7.4

Fert	1	2	3	4	5
100N	6.9	9.6	5.6	7.4	8.2
100N+75P	9.6	9.3	12.0	10.6	11.6
50N	7.3	NA	7.7	7.7	7.0
50N+75P	10.8	9.2	8.8	9.9	9.4
Unfertilised	5.6	6.1	5.3	5.9	7.4

È stato eseguito un esperimento a quadrato latino, per valutare l’effetto di quattro diversi fertilizzanti sulla resa della lattuga. I dati osservati sono disponibili come ‘lettuceLS’ e sono riportati nella tabella seguente. Qual è il fertilizzante migliore?

Fertiliser	Row	Column	Yield
A	1	1	155.5
B	1	2	128.4
C	1	3	105.5
D	1	4	182.4
A	2	4	185.4
B	2	3	163.8
C	2	1	178.4
D	2	2	238.3
A	3	3	173.1
B	3	4	170.0
C	3	2	198.6
D	3	1	213.3
A	4	2	185.7
B	4	1	198.9
C	4	4	191.7
D	4	3	231.6

È stato eseguito un esperimento in vaso per valutare il momento migliore per l’applicazione di un erbicida (rimsulfuron) contro Sorghum halepense da rizoma. Sono state confrontate cinque epoche d’intervento (2-3, 4-5, 6-7 e 8-9 foglie, oltre ad un intervento doppio a 3-4 e 8-9 foglie) e il controllo non trattato. Per comprendere se l’applicazione sia efficace contro piante provenienti da rizomi di diverse dimensioni, è stato incluso nell’esperimento un secondo fattore sperimentale, ovvero la dimensione del rizoma (2, 4, 6 nodi). Il disegno sperimentale era un fattoriale a due vie, completamente incrociato, con trattamenti completamente randomizzati con quattro repliche. I risultati (peso delle piante tre settimane dopo l’applicazione dell’erbicida) sono tratti da (Onofri, 1994b} e sono disponibili come ‘johnsongrass’. In quale momento l’erbicida è più efficace? Il doppio trattamento risulta più efficace dei trattamenti singoli? La raccomandazione per gli agricoltori può essere considerata univoca ed indipendente dalla dimensione del rizoma?

Sizes / Timings	2-3	4-5	6-7	8-9	3-4/8-9	Untreated
2-nodes	34.03	0.10	30.91	33.21	2.89	41.63
	22.31	6.08	35.34	43.44	19.06	22.96
	21.70	3.73	24.23	44.06	0.10	52.14
	14.90	9.15	28.27	35.34	0.68	59.81
4-nodes	42.19	14.86	52.34	39.06	8.62	68.15
	51.06	36.03	43.17	61.59	0.05	42.75
	43.77	21.85	57.28	48.89	0.10	57.77
	31.74	8.71	29.71	49.14	9.65	44.85
6-nodes	20.84	11.37	55.00	41.77	9.80	43.20
	26.12	2.24	28.46	37.38	0.10	40.68
	35.24	14.17	21.81	39.55	1.42	34.11
	13.32	23.93	60.72	48.37	6.83	32.21

Rep	A	B	C
1	456	118	72
2	411	213	99
3	594	74	24
4	280	26	20
5	664	163	89
6	379	76	47
7	444	240	32
8	436	75	29
9	294	108	1
10	431	68	33
11	476	108	20
12	382	153	22
13	413	98	27
14	485	120	39
15	440	126	12

Rep	A	B	C
1	456	118	72
2	411	213	99
3	594	74	24
4	280	26	20
5	664	163	89
6	379	76	47
7	444	240	32
8	436	75	29
9	294	108	1
10	431	68	33
11	476	108	20
12	382	153	22
13	413	98	27
14	485	120	39
15	440	126	12

Rep	A	B	C
1	456	118	72
2	411	213	99
3	594	74	24
4	280	26	20
5	664	163	89
6	379	76	47
7	444	240	32
8	436	75	29
9	294	108	1
10	431	68	33
11	476	108	20
12	382	153	22
13	413	98	27
14	485	120	39
15	440	126	12