Capitolo 4 Le relazioni causa-effetto
Nel capitolo precedente abbiamo visto come possiamo utilizzare semplici statistiche per descrivere alcuni tratti dei nostri dati sperimentali, come la tendenza centrale e la dispersione e, se abbiamo due o più variabili, abbiamo visto come possiamo descrivere la loro variabilità congiunta. Nel lavoro di ricerca, la relazione tra variabili più importante è la cosiddetta causalità, che si verifica ogni volta che una variabile (solitamente denominata “predittore”) provoca un cambiamento in un’altra variabile (solitamente denominata “risposta”); ad esempio, una variazione del genotipo può causare un cambiamento nella resa del frumento, oppure una variazione nella tecnica di lavorazione può causare un cambiamento nel tempo di emergenza del mais. Questo effetto diretto del predittore sulla risposta (e non viceversa) è ciò che rende la causalità diversa, ad esempio, dalla correlazione, che implica solo variazione congiunta, senza una chiara distinzione tra predittore e risposta, cioè tra la causa e l’effetto.
Gli esperimenti controllati, replicati e randomizzati sono particolarmente adatti a stabilire relazioni causa-effetto; infatti, la probabilità di effetti confondenti è ridotta al minimo, così che le discrepanze tra le unità osservate sottoposte a trattamenti diversi possono essere ragionevolmente attribuite all’effetto di tali trattamenti sperimentali e non ad altre cause sistematiche, ma ignote.
4.1 Modelli matematici e statistici
Per descrivere le relazioni causali, possiamo utilizzare i modelli statistici, cioè delle equazioni in cui le osservazioni sperimentali sono prodotte come risultato dell’effetto di uno o più predittori.
In effetti, questo approccio alla scienza è fondato sull’eredità galileiana, che ci porta ad immaginare che il funzionamento della natura sia descrivibile utilizzando il linguaggio universale della matematica. In effetti era proprio questa l’ambizione più grande degli scienziati all’inizio dell’ottocento: conoscendo lo stato iniziale di un sistema, doveva essere possibile prevederne con precisione l’evoluzione futura. Laplace diceva: “Possiamo considerare lo stato attuale dell’universo come l’effetto del suo passato e la causa del suo futuro. Un intelletto che ad un determinato istante dovesse conoscere tutte le forze che mettono in moto la natura, e tutte le posizioni di tutti gli oggetti di cui la natura è composta, se questo intelletto fosse inoltre sufficientemente ampio da sottoporre questi dati ad analisi, esso racchiuderebbe in un’unica formula i movimenti dei corpi più grandi dell’universo e quelli degli atomi più piccoli; per un tale intelletto nulla sarebbe incerto ed il futuro proprio come il passato sarebbe evidente davanti ai suoi occhi”. In realtà si è ben presto scoperto che si trattava di un’ambizione irrealistica, non tanto e non solo per la comparsa della meccanica quantistica un secolo dopo, ma anche per l’aumento di importanza degli studi in ambito psichiatrico e medico/biologico. Questi studi, infatti, venivano (e vengono) eseguiti su organismi viventi molto complessi, che, se sottoposti allo stesso stimolo, davano (e danno) risposte altamente variabili e, spesso, anche difficilmente misurabili e controllabili.
Queste difficoltà fecero prevalere, tra i biologi, la convinzione che la natura funzionasse in base a meccanismi deterministici ben definiti, anche se difficilmente osservabili nella pratica sperimentale, a causa dei numerosi elementi d’incertezza che si manifestavano nel corso delle osservazioni sperimentali. Insomma, la natura è perfetta, ma l’osservazione è fallace, perché influenzata dalla presenza di una forte componente stocastica ed imprevedibile, che va sotto il nome generico di errore sperimentale. Di questo abbiamo già parlato nei capitoli precedenti. Abbiamo anche visto che Ronald Fisher, nel suo famoso testo “Il disegno degli esperimenti” ha posto le basi per una corretta metodica sperimentale, finalizzata a minimizzare l’impatto della componente stocastica e, soprattutto, ad impedire che essa si confondesse con gli effetti degli stimoli sperimentali in studio.
Minimizzare, tuttavia, non significa eliminare ed è evidente che, pur con tutti gli sforzi possibili, è impossibile evitare che i risultati sperimentali siano influenzati, sempre e comunque, da una certa quota di variabilità stocastica. Si vengono quindi a creare due contrapposte situazioni:
- la verità ‘vera’, immanente, che ‘agisce’ in base a meccanismi deterministici causa-effetto ben definiti.
- La ‘verità’ sperimentale, che si produce a partire dalla verità ‘vera’, per effetto dell’azione di elementi perturbativi casuali, che non ci permettono di osservare la verità ‘vera’.
Di conseguenza, la descrizione di qualunque risultato sperimentale non può essere realistica se non utilizzando un modello in grado di considerare contemporaneamente sia i nessi causa-effetto, che le altre forze ignote e, almeno apparentemente, di natura stocastica. I modelli matematici che incorporano anche effetti di natura casuale sono detti modelli statistici.
4.2 Componenti di un modello
In semplice linguaggio algebrico, possiamo scrivere un modello causa-effetto utilizzando un’a funzione’equazione generale come la seguente:
\[ Y_E = f(X, \theta)\]
dove \(Y_E\) è l’effetto atteso dello stimolo \(X\), secondo la funzione \(f\), basata su una collezioni di parametri \(\theta\)
Le componenti di questo modello sono la risposta attesa (\(Y_E\)) che è l’oggetto del nostro studio e può assumere le forme più disparate: spesso è numerica, ma a volte rappresenta una qualità. In questo libro consideremo solo la situazione in cui \(Y_E\) è rappresentato da una sola variabile (analisi univariata), ma esistono casi in cui viene osservata ed analizzata la risposta di soggetti in relazione a molte variabili (analisi multivariata).
Lo stimolo sperimentale (\(X\)) è costituito da una o più variabili continue, discrete o categoriche (predittori), che rappresentano i trattamenti sperimentali. Insieme ad \(Y_E\), \(X\) è l’elemento noto di un esperimento, in quanto viene definito a priori in fase di progettazione.
La ‘funzione’ di risposta (\(f\)) è un’equazione, lineare o non-lineare, scelta in base a considerazioni di carattere biologico, o con un approccio puramente empirico, osservando l’andamento della curva di risposta.
I parametri di una funzione (\(\theta\)) sono un insieme di valori numerici che permettono di definire l’equazione di risposta.
Il predittore può essere rappresentato da una dose; ad esempio un aumento della dose di una sostanza erbicida provoca una diminuzione della crescita delle erbe infestanti. In questo caso usiamo il termine modello dose-risposta, che è forse uno dei modelli più famosi e risale a Paracelso (1493-1541), che coniò la sua famosa massima “Cosa c’è che non sia veleno? Tutte le cose sono veleno e nulla è senza veleno. Soltanto la dose determina che una cosa non è un veleno”.
Il modello sovrastante, in accordo con la logica galileiana, postula che un fenomeno naturale segua una legge ben definita. Tuttavia, la realtà è più complessa delle nostre aspettative e, a causa di errori sperimentali e altri effetti di natura puramente casuale, non osserviamo mai il risultato atteso \(Y_E\), ma osserviamo un valore diverso \(Y_O \neq Y_E\). Dobbiamo quindi ampliare il modello aggiungendo la componente stocastica \(\varepsilon\):
\[ Y_O = f(X, \theta) + \varepsilon\]
cioè il cosiddetto ‘residuo’, la discrepanza tra ciò che prevede il modello e ciò che effettivamente osserviamo:
\[\varepsilon = Y_O - Y_E \]
In un esperimento con \(n\) unità sperimentali, abbiamo \(n\) residui, con media pari a 0 e deviazione standard pari a \(\sigma\) (Root Mean Squared Error, ovvero l’RMSE o \(\sigma\)). In parole povere, i residui misurano quanto “cattivo” è il modello: più alti sono i residui, peggiore è la capacità del modello di descrivere una certa relazione causa-effetto.
4.3 Fitting di un modello
Nella ricerca, possiamo utilizzare i modelli per capire se due o più variabili sperimentali sono in una relazione causa-effetto tra di loro. Il nostro lavoro consisterà nel:
- definire un modello un modello statistico potenzialmente capace di descrivere adeguatamente le relazioni causa-effetto in studio. In altre parole si potrebbe dire che lo sforzo è quello di tradurre un’ipotesi scientifica in un modello statistico, per verificare se il modello è supportato dai dati, così come l’ipotesi scientifica di cui esso è la ‘traduzione’. Questo modello sarà posto nella sua forma generale e sarà basato su una serie di parametri dal valore ignoto (\(\theta\) e \(\sigma\)).
- Eseguire l’esperimento e raccogliere i dati;
- utilizzare il set di dati per assegnare valori precisi a tutti i parametri ignoti (fitting del modello o, in alcune applicazioni, calibrazione del modello);
- valutare se il modello parametrizzato fornisca una descrizione accurata dei dati sperimentali (valutazione del modello);
- se necessario, selezionare il modello migliore tra tutti quelli quelli possibili (confronto dei modelli).
Il fitting del modello viene solitamente eseguito dall’algoritmo dei “minimi quadrati”, che consiste nel selezionare i valori dei parametri che minimizzano la somma dei residui al quadrato:
\[RSS = \sum_{i = 1}^n{\left( Y_{O_i} - Y_{E_i} \right)^2}\]
In generale, la minimizzazione dei quadrati dei residui non viene eseguita mediante calcoli manuali, in quanto è molto più semplice avvalersi delle funzioni di adattamento più adatte in R. In particolare, per i modelli lineari utilizzeremo la funzione lm(), secondo la seguente sintassi:
mod <- lm(Y ~ X dati = set di dati)Il primo argomento è l’equazione che vogliamo adattare: sul lato sinistro dobbiamo specificare il nome della variabile di risposta, la ‘tilde’ (~) significa ‘è una funzione di’ e sostituisce il segno ‘=’, mentre, sul lato destro, dobbiamo specificare il nome del/i predittore/i. Come secondo argomento, se necessario, forniamo il nome del dataset in cui sono archiviate le variabili. Non dobbiamo specificare l’intercetta e il termine stocastico \(\varepsilon\), che sono inclusi per impostazione predefinita. C’è inoltre da tenere presente che, prima dell’analisi, ogni volta che vogliamo utilizzare una variabile numerica come fattore, dovremmo eseguire esplicitamente questa trasformazione utilizzando la funzionottenere risultati sbagliati (come vedremo nei capitoli seguenti).
Un modello causa-effetto completamente specificato può fornire una buona descrizione dei dati sperimentali, postulando l’esistenza di un meccanismo causa-effetto che produce i risultati sperimentali. Con la dovuta prudenza, questo modello può essere utilizzato per fare previsioni; ad esempio, il modello precedente suggerisce che una fertilizzazione con azoto di 150 kg/ha dovrebbe, prevedibilmente, dare come risultato un livello di resa \(Y_E = 65\) quintali per ettaro.
4.4 Esempio 1: il ‘modello della media’
Abbiamo condotto un esperimento misurativo, in cui abbiamo raccolto tre campioni di acqua da un pozzo, per misurare la concentrazione di una sostanza xenobiotica. I risultati sono 116, 119, 125 mg/L e vogliamo calcolare la media e la deviazione standard dei tre campioni.
Questo problema è piuttosto semplice e potrebbe essere meglio risolto utilizzando semplici statistiche descrittive (vedi Capitolo 3); tuttavia, è interessante vedere come lo stesso problema può essere risolto con un’operazione di ‘model fitting’: non abbiamo alcun predittore e, pertanto, possiamo supporre che le osservazioni siano generate in base al modello della media, che abbiamo mostrato in precedenza (\(Y_i = \mu + \varepsilon_i\)).
Assegnare un valore a tutti i parametri sconosciuti è banale, utilizzando i semplici calcoli mostrati nel Capitolo 3 (vale a dire, \(\mu = 120\) e \(\sigma = 4.58\)). Tuttavia, possiamo ottenere gli stessi risultati utilizzando l’approccio di minimizzazione dei minimi quadrati, come mostrato nel riquadro seguente. Si noti che utilizziamo ‘1’ come lato destro dell’equazione del modello, poiché non abbiamo alcun predittore.
Y <- c(116, 119, 125)
mod <- lm(Y ~ 1)La stima di \(\mu\) può essere ottenuta con la seguente funzione R:
coef(mod)
## (Intercept)
## 120Per quanto riguarda la componente stocastica, possiamo ottenere i residui, la loro devianza e la loro deviazione standard con le seguenti funzioni R:
# Residui
residuals(mod)
## 1 2 3
## -4 -1 5
#
# Devianza dei residui
deviance(mod)
## [1] 42
#
# Deviazione standard dei residui
summary(mod)$sigma
## [1] 4.582576Il modello della media descrive una situazione in cui non abbiamo predittori e, pertanto, non vi sono nessi causa-effetto; di conseguwnza, è il peggior modello possibile, il punto di riferimento rispetto al quale valutare ogni altro modello alternativo. Per queste sue caratteristiche, il modello della media è spesso definito come modello nullo.
4.5 Esempio 2: un predittore quantitativo
L’algoritmo dei minimi quadrati è facile da comprendere se consideriamo un’indagine in cui la resa del mais (in q/ha) è stata determinata, come conseguenza della copertura delle erbacce, all’inizio del ciclo colturale. In una situazione del genere, potremmo aspettarci una relazione causa-effetto, in cui la copertura delle erbacce è il predittore e la resa è la risposta, secondo la funzione lineare (linea retta) \(Y_i = b_0 + b_1 \, Xx_i + \varepsilon_i\), che è solitamente nota come modello di regressione semplice.
I due parametri \(b_0\) e \(b_1\) rappresentano, rispettivamente, l’intercetta (livello di resa senza erbacce) e la pendenza (variazione della resa per un aumento di 1 unità nella copertura delle erbacce). Per stimare questi due valori, possiamo usare la funzione ‘lm()’ (riquadro codice 4.2), che produce i risultati mostrati nella Figura 4.1.
# Code box 4.2
# Fitting a simple linear regression model
# Entering the data
yield <- c(29.8, 88.9, 47.0, 96.6, 83.0, 95.3, 91.5, 97.9,
89.2, 88.3, 96.9, 93.9, 84.6, 51.9, 21.8, 35.7)
weedCover <- c(105.35, 27.5, 68.8, 23.8, 12.7, 42.7, 31.5,
37.8, 18.9, 35.8, 44.5, 11.4, 31.6, 87.9,
133.9, 136.525)
# Fitting the model
mod <- lm(yield ~ weedCover)
# Inspecting the estimates
coef(mod)
## (Intercept) weedCover
## 106.5979798 -0.6033652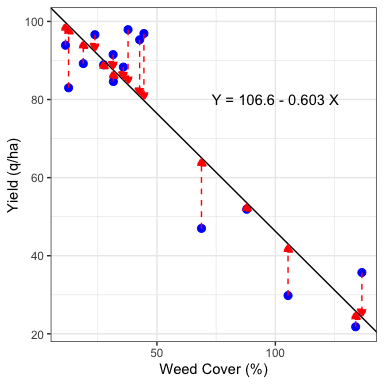
Figura 4.1: Example 2: the least square estimate is represented by the straight line that passes as close as possible to the observed points.
4.6 Esempio 3: un predittore nominale
Immaginiamo un esperimento sul campo per confrontare la resa di quattro genotipi di avena (denominati A, B, C e D), con un disegno completamente randomizzato con tre repliche. I risultati (in tonnellate per ettaro) sono mostrati nella Tabella 4.1.
| A | 4.5 | 4.3 | 4.8 |
| B | 3.9 | 3.6 | 4.0 |
| C | 3.9 | 4.2 | 4.3 |
| D | 4.6 | 4.7 | 5.0 |
In questo esperimento, abbiamo una risposta quantitativa (la resa) e un fattore nominale (il genotipo) e la relazione causa-effetto tra queste due variabili può essere descritta con il modello seguente:
\[Y_i = \mu + \alpha_j + \varepsilon_i\]
Questo modello postula che ogni osservazione \(Y_i\) derivi dal valore \(\mu\) (la cosiddetta intercetta) più le quantità \(\alpha_j\), che dipendono dal genotipo \(j\), più gli effetti stocastici \(\varepsilon_i\), che sono specifici per ogni osservazione ed hanno media 0 e una deviazione standard pari a \(\sigma\).
Per comprendere il significato biologico di \(\mu\) ed \(\alpha\) dobbiamo entrare un po’ di più nei dettagli matematici. Consideriamo la prima osservazione \(Y_1 = 4.5\); dobbiamo stimare tre valori (\(\mu\), \(\alpha_1\) e \(\varepsilon_1\)) che, sommati, restituiscano questa osservazione. Chiaramente il problema è indeterminato, in quanto esistono infinite triplette di valori, che, sommate, restituiscono 4.5; pertanto è necessario imporre dei vincoli su alcuni parametri del modello (parametrizzazioni del modello). Un vincolo molto comune è \(\alpha_1 = 0\) (vincolo sul trattamento):
\[\left\{ {\begin{array}{l} \mu_1 = \mu + \alpha_1 = \mu + 0\\ \mu_2 = \mu + \alpha_2 \\ \mu_3 = \mu + \alpha_3 \\ \mu_4 = \mu + \alpha_4 \end{array}} \right.\]
Con tale vincolo, \(\mu\) è la media del primo genotipo (in R: primo in ordine alfabetico), mentre \(\alpha_2\), \(\alpha_3\) e \(\alpha_4\) sono, rispettivamente, le differenze tra le medie del secondo, terzo e quarto genotipo, rispetto al primo. In generale, con questa parametrizzazione, i parametri del modello sono medie o differenze tra medie.
Un altro possibile vincolo è \(\sum{\alpha_j} = 0\) (vincolo sulla somma). Se prendiamo l’equazione precedente e sommiamo tutti i membri otteniamo:
\[\mu_1 + \mu_2 + \mu_3 + \mu_4 = 4 \mu + \sum{\alpha_j}\]
Imponendo il vincolo di somma a zero otteniamo:
\[\mu_1 + \mu_2 + \mu_3 + \mu_4 = 4 \mu\]
e quindi a:
\[\mu = \frac{\mu_1 + \mu_2 + \mu_3 + \mu_4}{4}\]
Con questa parametrizzazione \(\mu\) è la media generale dei dati, mentre i valori \(\alpha_j\) rappresentano le differenze tra le medie dei trattamenti e la media generale (effetti dei trattamenti): valori \(\alpha\) positivi ed elevati identificano i genotipi superiori alla media, mentre valori \(\alpha\) elevati, ma negativi identificano i genotipi inferiori alla media. In generale, con questa parametrizzazione, i parametri del modello rappresentano medie ed effetti.
Un terzo possibile vincolo si ottiene rimuovendo l’intercetta (ovvero, imponendo che \(\mu = 0\)). In questo caso, i valori di \(\alpha_j\) saranno le medie dei genotipi ed il modello riduce a:
\[Y_i = \mu_j + \varepsilon_i\]
La selezione dei vincoli spetta all’utente, a seconda degli obiettivi dell’esperimento. In R, il vincolo del trattamento è utilizzato di default, sebbene gli altri vincoli possano essere facilmente ottenuti, utilizzando la codifica appropriata.
La stima dei parametri del modello potrebbe essere facilmente eseguita a mano, ma noi utilizziamo la funzione ‘lm()’ in R.
Yield <- c(4.5, 4.3, 4.8,
3.9, 3.6, 4.0,
3.9, 4.2, 4.3,
4.6, 4.7, 5.0)
Genotype <- rep(LETTERS[1:4], each = 3)
mod <- lm(Yield ~ Genotype)I parametri stimati, i residui, la deviazione residua e la deviazione standard possono essere ottenuti con la solita codifica:
# Stima dei parametri
coef(mod)
## (Intercept) GenotypeB GenotypeC GenotypeD
## 4.5333333 -0.7000000 -0.4000000 0.2333333
#
# Residui
residuals(mod)
## 1 2 3 4 5
## -0.03333333 -0.23333333 0.26666667 0.06666667 -0.23333333
## 6 7 8 9 10
## 0.16666667 -0.23333333 0.06666667 0.16666667 -0.16666667
## 11 12
## -0.06666667 0.23333333
#
# Devianza dei residui
deviance(mod)
## [1] 0.3866667
#
# Deviazione standard del residui (RMSE)
summary(mod)$sigma
## [1] 0.2198484Ora che il modello è completamente specificato, abbiamo tutti gli ingredienti per descrivere le 12 osservazioni, sommando \(\mu + \alpha_j + \varepsilon_i\); ad esempio, per la prima osservazione, appartenente al primo genotipo, abbiamo:
\[y_1 = 4.5 = 4.533 + 0 - 0.033\] mentre, per la quarta osservazione, appartenente al 2° genotipo, abbiamo:
\[y_4 = 3.9 = 4.533 - 0.7 + 0.067\]
Per completezza, potrebbe essere utile mostrare che, in R, possiamo modificare la parametrizzazione, impostando l’argomento ‘contrasts’ e passando un elenco di fattori associati alla parametrizzazione richiesta. Ad esempio, se utilizziamo Treat = "contr.sum", otteniamo il vincolo sulla somma; di conseguenza, l’effetto dell’ultimo genotipo non è mostrato, perché è vincolato ad eseere l’opposto della somma degli altri tre effetti.
mod2 <- lm(Yield ~ Genotype,
contrasts = list(Genotype = "contr.sum"))
coef(mod2)
## (Intercept) Genotype1 Genotype2 Genotype3
## 4.3166667 0.2166667 -0.4833333 -0.1833333Un’altra possibile parametrizzazione consiste nel rimuovere l’intercetta, che è possibile utilizzando -1 sul lato destro dell’espressione, come mostrato di seguito.
mod3 <- lm(Yield ~ Genotype - 1)
coef(mod3)
## GenotypeA GenotypeB GenotypeC GenotypeD
## 4.533333 3.833333 4.133333 4.766667Esistono diversi altri metodi per modificare la parametrizzazione, sia globalmente (per l’intera sessione R) sia a livello di fattore; ulteriori informazioni sono disponibili in letteratura.
4.7 L’analisi della varianza (ANOVA)
In questo secondo esempio abbiamo descritto una relazione causa-effetto, tramite un modello contenente un predittore. L’RMSE (\(\sigma\)) è uguale a 0.220, ma questa non è una buona metrica per capire se la relazione causa-effetto è rilevante o meno. Una possibilità è quella di dividere l’RMSE per la media dei valori osservati, per ottenere il coefficiente di variabilità (RRMSE: Relative Root Mean Squared Error), che è 0.051 (o 5.1%), il che indica che l’errore residuo è piuttosto piccolo, rispetto al valore medio atteso.
Un altro indicatore per descrivere la bontà della relazione causa-effetto definita dal modello è il cosiddetto coefficiente di determinazione (R2), ottenuto sottraendo da 1 il rapporto tra la devianza dei residui e la devianza totale delle osservazioni (che poi sarebbe la devianza dei residui del modello nullo). Nel nostro caso, il modello nullo è ottenuto trascurando l’effetto del genotipo e la devianza dei residui è quella indicata nel box sottostante:
modnull <- lm(Yield ~ 1)
deviance(modnull)
## [1] 1.936667Il coefficiente di determinazione è quindi:
\[R^2 = 1 - \frac{SS_{res}}{SS_{tot}} = 1 - \frac{0.3866667}{1.936667} = 0.800\]
cosa che può essere verificata utilizzando il codice R:
summary(mod)$r.squared
## [1] 0.8003442Il coefficiente di determinazione varia da 0 ad 1, più è alto il valore tanto migliore è la bontà del modello.
Oltre a queste statistiche (RMSE, RRMSE e R2), vi è una tecnica famosissima per valutare l’entità dell’evidenza in favore dell’esistenza di una relazione causa effetto ben definita; questa tecnica si chiama Analisi della Varianza (ANOVA) ed è stata originariamente ideata da Ronald Fisher durante gli anni ’30 del XX secolo; oggi è ancora molto utilizzata, seppure in una forma leggermente diversa da quella originale.
Il principio di fondo è che, considerando un modello che contenga almeno un predittore, è sempre possibile associare allo stesso dataset un secondo modello ‘nullo’ (modello della media), ottenuto dal precedente per rimozione del predittore. Ad esempio, con riferimento all’esempio 2, abbiamo già visto che il modello ANOVA è:
Yield ~ Genotypementre il modello nullo è:
Yield ~ 1Rimuovere l’effetto del genotipo dal modello npn può che indurre un incremento dei residui, dato che non si tiene più in considerazione il fatto che parte della differenza tra le osservazioni è dovuto al fatto che esse appartengono a genotipi di versi. Infatti, il codice sovrastante e sottostante mostrano che la devianza dei residui (RSS: Residual Sum of Squares) è pari a:
epsilon <- residuals(mod)
RSS <- sum(epsilon^2)
RSS
## [1] 0.3866667mentre la devianza dei residui del modello nullo (pari alla devianza totale delle osservazioni), è pari a:
# Residual deviance null model
RSS.null <- sum(residuals(modnull)^2)
RSS.null
## [1] 1.936667Insomma, rimuovendo l’effetto del genotipo, il modello è ‘peggiorato’, con un incremento dei residui quantificabile come differenza:
# Contribution of genotype effect
SS_g <- RSS.null - RSS
SS_g
## [1] 1.55È evidente che più è grande questa differenza, più è grande l’effetto del genotipo. In altre parole, abbiamo appena scomposto la devianza totale delle osservazioni (\(SS_{tot} = 1.937\)) in due quote, una dovuta all’effetto causale del trattamento sperimentale (\(SS_g = 1.55\)) e l’altra dovuta a tutti gli altri effetti ignoti di natura casuale (errore sperimentale: \(RSS = 0.387\)). Questa seconda quota costituisce una specie di ‘rumore di fondo’, contro il quale si può valutare il ‘segnale’, cioè l’intensità dell’effetto del trattamento sperimentale.
Come abbiamo visto nel Capitolo 3, non possiamo confrontare direttamente \(SS_g\) e \(RSS\), poiché queste due devianze hanno un diverso numero di gradi di libertà (DF); il numero di DF per il trattamento è uguale al numero dei suoi livelli meno uno (\(DF_g\) = 3), mentre il numero di gradi di libertà per la devianza residua \(RSS\) è \(p \times (k -1)\), dove \(p\) è il numero di trattamenti e \(k\) è il numero di repliche, supponendo che questo sia costante tra i trattamenti. Di conseguenza, \(DF_{RSS} = 4 \times (3 - 1) = 8\). Possiamo quindi calcolare le relative varianze (Qudrati Medi: MS) come segue:
# Varianza del genotipo
MS_g <- SS_g/3
MS_g
## [1] 0.5166667
#
# Varianza del residuo
RMS <- RSS/8
RMS
## [1] 0.04833333Queste due varianze (trattamento e residuo) possono essere confrontate direttamente, utilizzando il cosiddetto rapporto F:
\[F = \frac{MS_g}{RMS} = \frac{0.517}{0.048} = 10.69\]
Il nome ‘rapporto F’ deriva da Fisher, che lo inventò. Mostra che la variabilità imposta dal trattamento sperimentale è più di 10 volte superiore alla variabilità dovuta al rumore di fondo (errore sperimentale), il che supporta l’idea che l’effetto causale del genotipo sulla resa sia molto rilevante. In termini generali, più alto è il rapporto F, più forte è il nesso causa-effetto. Possiamo riassumere questi risultati nella cosiddetta tabella ANOVA, che si ottiene facilmente utilizzando il metodo ‘anova()’ con R.
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Genotype 3 1.55000 0.51667 10.69 0.003584 **
## Residuals 8 0.38667 0.04833
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Rispetto a quanto esposto in precedenza, la tabella ottenuta con R contiene solo un valore che non abbiamo ancora spiegato, il cosidetto P-level, che si trova all’estrema destra (P = 0.003584). Si tratta di un indicatore inferenziale che sarà illustrato nei Capitoli seguenti anche se è opportuno dare ora indicazioni per la sua interpretazione. In dettaglio, più il P-level è basso, più è forte l’evidenza scientifica contro l’ipotesi ‘nulla’ che il trattamento sperimentale (in questo caso il genotipo) non abbia avuto alcun effetto sulla variabile risposta (produzione della coltura). Ancora più in dettaglio, se il P-level è inferiore a 0.05 ed è accompagnato da uno o più asterischi, la conclusione è che l’effetto del trattamento è statisticamente significativo.
4.8 Example 4: due predittori nominali
Consideriamo lo stesso esperimento dell’esempio precedente ed immaginiamo che sia stato disegnato a blocchi randomizzati (la prima osservazione di ogni genotipo è stata presa nel primo blocco, la seconda nel secondo blocco e così via). In questo caso, il nesso causa-effetto e, di consegeunza, il modello interpretativo sono diversi, perché la resa dipende da due fattori sperimentali, ovvero il genotipo e il blocco. L’equazione è:
\[ Y_{ij} = \mu + \gamma_i + \alpha_j + \varepsilon_{ij}\]
dove \(Y_{ij}\) è la resa parcellare nell’ \(i\)esimo blocco e per il \(j\)esimo genotipo, \(\mu\) è l’intercetta, \(\gamma_i\) è l’effetto del \(i\)esimo blocco, \(\alpha_j\) è l’effetto del \(j\)esimo genotipo e \(\varepsilon\) è l’errore residuo di ogni parcella, con deviazione standard pari a \(\sigma\). Come abbiamo fatto per il modello ANOVA ad una via, dobbiamo porre dei vincoli sui valori \(\alpha\) e \(\gamma\), in modo che i parametri del modello siano stimabili; in particolare, imporremo che \(\alpha_1 = \gamma_1 = 0\), in modo che \(\mu\) è la produzione nel primo blocco e col primo genotipo (in R, convenzionalmente il primo in ordine alfabetico). Abbiamo quindi 3 parametri da stimare per l’effetto del genotipo e 2 parametri da stimare per l’effetto del blocco, oltre a \(\sigma\).
La stima dei parametri del modello può essere eseguita con R, aggiungendo l’effetto blocco all’equazione del modello:
# I dati sono stati inseriti in un box precedente,
# qui creiamo il vettore che identifica il blocco
Block <- rep(LETTERS[1:3], times = 4)
mod <- lm(Yield ~ Genotype + Block)Le stime dei parametri sono:
# Alpha e beta
coef(mod)
## (Intercept) GenotypeB GenotypeC GenotypeD BlockB
## 4.4416667 -0.7000000 -0.4000000 0.2333333 -0.0250000
## BlockC
## 0.3000000
#
# Sigma
summary(mod)$sigma
## [1] 0.1443376I residui e la loro devianza sono:
epsilon <- residuals(mod)
RSS <- sum(epsilon^2)
RSS
## [1] 0.125Come previsto, i residui di questo modello sono più piccoli e quindi hanno una devianza minore di quelli del modello precedente, senza l’effetto del blocco. La rimozione dell’effetto del blocco fa si che la devianza del residuo aumenti da 0.125 a 0.38667 (vedi sopra), con una differenza pari a 0.262, che misura appunto l’effetto del blocco 8devianza del blocco: SSb). Anche in questo caso, se consideriamo un modello ridotto, contenente solo il blocco, ma non il genotipo (quindi rimuoviamo dal modello l’effetto del genotipo), possiamo misurare la devianza del fattore sperimentale rimosso, che, coerentemente con quanto visto in precedenza, ammonta a 1.55.
# Rimozione dei blocchi
mod2 <- lm(Yield ~ Genotype) # Stesso modello di prima
deviance(mod2)
## [1] 0.3866667
SS_b <- deviance(mod2) - RSS
SS_b
## [1] 0.2616667
# Rimozione dei genotipi
mod3 <- lm(Yield ~ Block)
deviance(mod3)
## [1] 1.675
SS_g <- deviance(mod3) - RSS
SS_g
## [1] 1.55Il numero di gradi di libertà è, rispettivamente, 11 per la devianza totale (\(SS_{tot} = n - 1 = 12 - 1 = 11\)), 3 per i genotipi (numero dei genotipi meno 1) e 2 per i blocchi (numero dei blocchi meno 1); per sottrazione, arriviamo a 6 DF per la devianza del residuo. A questo punto possiamo calcolare le varianze dei blocchi, dei genotipi e del residuo, che anche in questo caso è attribuibile a tutte le sorgenti di variabilità casuali non controllate (errore sperimentale o rumore di fondo). In questo caso possiamo calcolare due rapporti F, uno per l’effetto del blocco e uno per l’effetto del genotipo; per comodità, possiamo saltare tutti i calcoli manuali e arrivare direttamente alla tabella ANOVA finale usando il metodo ‘anova()’ in R.
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Genotype 3 1.55000 0.51667 24.80 0.0008833 ***
## Block 2 0.26167 0.13083 6.28 0.0337847 *
## Residuals 6 0.12500 0.02083
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1I rapporti F suggeriscono che l’effetto causale del genotipo è elevato e significativo (presenza di asterischi), mentre l’effetto blocco è significativo, ma il valore F è più basso e P è più alto di quello del genotipo, il che porta a pensare che l’effetto prodotto dal blocco sia meno rilevante.
4.9 Example 5: due predittori nominali con interazione
Immaginiamo che l’esperimento presentato nell’Esempio 1 sia stato ripetuto in un’altra località, utilizzando sempre un disegno completamente randomizzato. I dati osservati sono riportati nella Tabella 4.2.
| Genotype | Location | Yield |
|---|---|---|
| A | LOC1 | 4.5 |
| A | LOC1 | 4.3 |
| A | LOC1 | 4.8 |
| B | LOC1 | 3.9 |
| B | LOC1 | 3.6 |
| B | LOC1 | 4.0 |
| C | LOC1 | 3.9 |
| C | LOC1 | 4.2 |
| C | LOC1 | 4.3 |
| D | LOC1 | 4.6 |
| D | LOC1 | 4.7 |
| D | LOC1 | 5.0 |
| A | LOC2 | 5.4 |
| A | LOC2 | 5.5 |
| A | LOC2 | 4.1 |
| B | LOC2 | 5.8 |
| B | LOC2 | 7.1 |
| B | LOC2 | 5.8 |
| C | LOC2 | 4.2 |
| C | LOC2 | 4.5 |
| C | LOC2 | 4.8 |
| D | LOC2 | 5.0 |
| D | LOC2 | 6.2 |
| D | LOC2 | 5.6 |
In questo esperimento abbiamo due fattori incrociati, ma, a differenza dell’esempio precedente, abbiamo tre repliche per ciascuna delle otto combinazioni tra i livelli di genotipo e località. In questo modo, oltre agli effetti di genotipo e località, possiamo anche valutare la cosiddetta interazione tra i due fattori sperimentali, che è un’informazione molto importante.
4.10 Interazione tra fattori sperimentali
Per comprendere meglio il concetto di interazione, osserviamo la Figura 4.2, dove sono mostrate le medie di quattro trattamenti, ottenuti dalla combinazione fattoriale di un trattamento A con due livelli (A1 e A2) e di un trattamento B con altrettanti livelli (B1 e B2). Nel grafico, ogni combinazione è rappresentata da un simbolo.
Concentriamoci un attimo sul grafico di sinistra e consideriamo la prima combinazione in ordine alfabetico (A1B1): per questa, la media è pari a 10. Se passiamo da A1 ad A2, fermo restando B1, l’incremento è + 4. Se invece passiamo da B1 a B2, fermo restando A1, l’incremento è + 5. Si deduce che, se gli effetti fossero puramente additivi, la media di A2B2 dovrebbe essere pari a 10 + 4 + 5 = 19, in quanto vengono modificati entrambi i livelli, da A1 ad A2 e da B1 a B2. Vediamo che l’osservazione conferma questa aspettativa di additività degli effetti e di mancanza di interazione.
Al contrario, nel grafico centrale vediamo che il risultato osservato di A2B2 non può essere ottenuto per semplice somma di effetti, perché, a fronte di un risultato atteso pari a 19 otteniamo invece 16. Evidentemente, vi è qualcosa in questa combinazione che altera l’effetto congiunto di A e B. Questo qualcosa può essere quantificato con il valore -3, così che la media A2B2 è pari a 10 + 4 + 5 - 3 = 16. Il valore -3 rappresenta la mancanza di additività o interazione; in questo caso si tratta di interazione semplice, in quanto la graduatoria dei trattamenti non cambia: A2 è sempre meglio di A1 e B2 è sempre meglio di B1, anche se gli effetti non sono quelli previsti.
Nel grafico di sinistra la situazione è analoga, ma più estrema: l’effetto dell’interazione è -10 e comporta un’inversione della graduatoria, per cui parliamo di interazione cross-over.
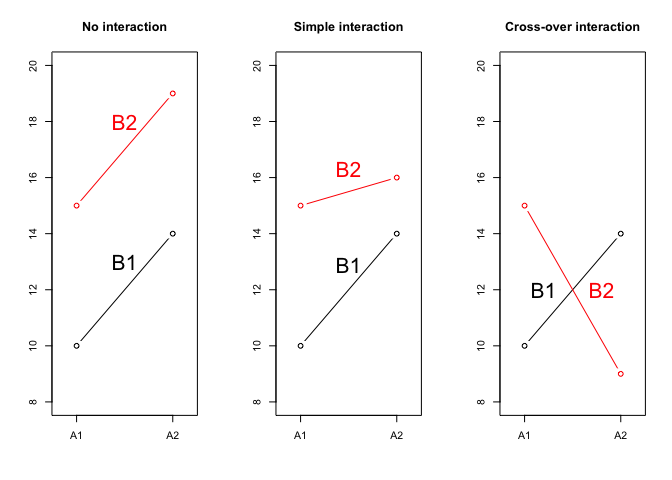
Figura 4.2: Esempi di interazione tra fattori sperimentali
Perchè siamo così interessati all’interazione e, in particolare, all’interazione cross-over? Esaminiamo più da vicino i valori nel grafico a destra in Figura 4.2, riportandoli nella tabella 4.3, insieme alle medie dei quattro livelli A1, A2, B1 e B2. Le medie delle combinazioni sono dette medie di cella, mentre le medie dei livelli principali sono dette medie marginali, perché si trovano al margine della tabella.
| B1 | B2 | Media | |
|---|---|---|---|
| A1 | 10.0 | 15.0 | 12.0 |
| A2 | 14.0 | 9.0 | 12.0 |
| Media | 12.5 | 11.5 | 12.0 |
Se guardassimo solo le medie marginali, avremmo l’impressione sbagliata che il fattore A, da solo, non ha alcun effetto (le medie A1 e A2 sono uguali) e che il fattore B ha solo un piccolissimo effetto. La realtà è invece che entrambi i fattori hanno un grande effetto, ma la presenza dell’interazione lo nasconde completamente, impedendoci di raggiungere conclusioni attendibili guardando ai due fattori, uno separatamente dall’altro.
4.11 Example 5 (segue)
Tornando al nostro esempio, è chiaro che le produzioni osservate sono determinate dall’effetto di:
- genotipo
- località
- interazione ‘genotipo \(\times\) località’
Il modello lineare può essere così definito:
\[Y_{ij} = \mu + \alpha_i + \beta_j + \alpha\beta_{ij} + \varepsilon_{ij}\]
dove \(\mu\) è l’intercetta (produzione del primo genotipo nella prima località, sotto il vincolo che \(\alpha_1 = \beta_1 = 0\)), \(\alpha_i\) è la differenza tra il genotipo \(i\)esimo ed il primo in ordine alfabetico, \(\beta_j\) è la differenza tra la località \(j\)esima e la prima in ordine alfabetico e \(\alpha\beta_{ij}\) è l’interazione tra il genotipo \(i\)esimo e la località \(j\)esima (sotto i vincoli che \(\alpha\beta_{1.} = \alpha\beta_{.1} = 0\)). I residui sono quantificati dai valori \(\varepsilon_{ij}\), con media uguale a 0 e deviazione standard uguale a \(\sigma\).
Per stimare i parametri del modello, possiamo utiliozzare R, considerando che il termine di interazione viene codificato con l’operatore ‘:’, ad esempio:
Y ~ A + B + A:Bche può essere abbreviato come:
Y ~ A * BYield <- c(4.5, 4.3, 4.8,
3.9, 3.6, 4.0,
3.9, 4.2, 4.3,
4.6, 4.7, 5.0,
5.4, 5.5, 4.1,
5.8, 7.1, 5.8,
4.2, 4.5, 4.8,
5.0, 6.2, 5.6)
Genotype <- rep(rep(LETTERS[1:4], each = 3), 2)
Location <- rep(c("LOC1", "LOC2"), each = 12)
dfr <- data.frame(Genotype, Location, Yield)
mod <- lm(Yield ~ Genotype * Location, data = dfr)
# Stima dei parametri
coef(mod)
## (Intercept) GenotypeB GenotypeC
## 4.5333333 -0.7000000 -0.4000000
## GenotypeD LocationLOC2 GenotypeB:LocationLOC2
## 0.2333333 0.4666667 1.9333333
## GenotypeC:LocationLOC2 GenotypeD:LocationLOC2
## -0.1000000 0.3666667
#
# Sigma
summary(mod)$sigma
## [1] 0.4765326L’analisi della varianza viene eseguita rimuovendo dal modello i tre termini uno alla volta, ma rispettando un criterio di marginalità, che tenga conto del fatto che l’interazione viene dopo che sono stati inseriti gli effetti principali che la costituiscono e, quindi, dovrebbe essere omessa per prima e non dovrebbe essere lasciata nel modello, quando uno degli effetti principali coinvolti viene rimosso. Lo schema è illustrato nel box seguente.
RSS <- deviance(mod)
#
# rimozione dell'interazione
modred <- lm(Yield ~ Genotype + Location, data = dfr)
SSint <- deviance(modred) - RSS
SSint
## [1] 4.008333
#
# rimozione del genotipo E dell'interazione
modred <- lm(Yield ~ Location, data = dfr)
SSloc <- deviance(modred) - RSS - SSint
SSloc
## [1] 2.601667
#
# rimozione della località E dell'interazione
modred <- lm(Yield ~ Genotype, data = dfr)
SSgen <- deviance(modred) - RSS - SSint
SSgen
## [1] 6.201667Anche in questo esempio, abbiamo suddiviso la variabilità totale dei dati in quattro termini, tre dei quali sono correlati all’effetto causale, mentre il quarto è correlato a tutti gli altri effetti casuali. In pratica, i calcoli manuali non sono necessari, perchè possiamo utilizzare la funzione ‘anova()’ in R. Nella tabella sottostante, l’unico elemento di cui non abbiamo parlato finora è il numero di gradi di libertà per l’interazione, che è uguale al prodotto del numero di DF per gli effetti principali.
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Genotype 3 2.6017 0.8672 3.8190 0.03077 *
## Location 1 6.2017 6.2017 27.3101 8.322e-05 ***
## Genotype:Location 3 4.0083 1.3361 5.8838 0.00662 **
## Residuals 16 3.6333 0.2271
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vediamo che tutti gli effetti in gioco (genotipo, località ed interazione) sono significativi ed hanno quindi un nesso causa-effetto rilevante sulla produzione della coltura. La presnza di un’interaione significativa mostra che, probabilmente, la valutazione dei genotipi performanti non è comune alle due località anche se questa affermazione richiede analisi successive che vedremo in seguito.
4.12 Dati non bilanciati
Prima di concludere questo capitolo, è necessario sottolineare che esistono diversi metodi per calcolare la somma dei quadrati per gli effetti del modello e che non portano necessariamente agli stessi risultati, in particolare quando i dati sono non bilanciati, ovvero quando c’è un numero diverso di repliche per ogni gruppo di trattamento. Il metodo da noi proposto si basa su:
- adattamento del modello completo ai dati osservati
- rimozione dell’effetto in studio e adattamento del modello ridotto
- sottrazione della somma residua dei quadrati del modello completo dalla somma residua dei quadrati del modello ridotto.
Questo approccio produce la cosiddetta somma marginale dei quadrati e non è lo stesso dell’approccio utilizzato nella funzione ‘anova()’ in base R, che produce la cosiddetta somma sequenziale dei quadrati. Questi due metodi danno gli stessi risultati con dati bilanciati, sebbene, con dati non bilanciati, raccomandiamo la somma marginale dei quadrati, che può essere ottenuta utilizzando la funzione ‘Anova()’ (si noti la lettera maiuscola all’inizio) nel pacchetto ‘car’, come mostrato nel seguente esempio.
4.13 Esempio 6: un CRBD con un valore mancante
Se consideriamo i dati nel precedente Esempio 3 e se immaginiamo che il genotipo A manchi dal terzo blocco (vedere il valore ‘NA’ nel riquadro Codice 4.14, che significa Non disponibile), il metodo ‘anova()’ in base R porta a diverse tabelle ANOVA, a seconda dell’ordine con cui i due effetti (genotipo e blocco) vengono inseriti nel modello (vedere riquadro Codice 4.14). Poiché non abbiamo una logica per decidere quale effetto debba essere inserito per primo, le conclusioni che otteniamo con la funzione ‘anova()’ sono puramente arbitrarie, il che non è accettabile nella scienza.
# Codice box 4.14
# Dati non bilanciati
Yield <- c(4.5, 4.3, NA,
3.9, 3.6, 4.0,
3.9, 4.2, 4.3,
4.6, 4.7, 5.0)
Genotype <- rep(LETTERS[1:4], each = 3)
Block <- rep(LETTERS[1:3], times = 4)
# Adattamento di un modello
mod1 <- lm(Yield ~ Genotype + Block)
mod2 <- lm(Yield ~ Block + Genotype)
# Partizionamento della varianza
anova(mod1)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Genotype 3 1.40182 0.46727 19.7671 0.003338 **
## Block 2 0.16181 0.08090 3.4224 0.115770
## Residuals 5 0.11819 0.02364
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mod2)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Block 2 0.10765 0.05383 2.277 0.198135
## Genotype 3 1.45597 0.48532 20.531 0.003061 **
## Residuals 5 0.11819 0.02364
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1L’approccio proposto in precedenza, basato sulla rimozione dei due predittori, uno alla volta, porta alla somma dei quadrati mostrata nel Codice box 4.15 e possiamo notare che questa somma di quadrati (per gli effetti genotipo e blocco) sono gli stessi, indipendentemente dall’ordine con cui i due effetti sono stati inclusi nel modello completo. Queste somme marginali di quadrati possono essere riprodotte utilizzando la funzione ‘Anova()’ nel pacchetto ‘car’ e impostando l’argomento ‘type = 2’. Ulteriori informazioni sui tipi di somma di quadrati possono essere trovate in Lansrud (2003).
# Casella di codice 4.15
# Rimozione dei predittori uno alla volta (modello 1)
RSS <- deviance(mod1)
mod1.red <- lm(Yield ~ Block) # Rimozione del genotipo
SS_g <- deviance(mod1.red) - RSS
SS_g
## [1] 1.455972
mod1.red2 <- lm(Yield ~ Genotype) # Rimozione del blocco
SS_b <- deviance(mod1.red2) - RSS
SS_b
## [1] 0.1618056
# Rimozione dei predittori uno alla volta (modello 2)
RSS <- deviance(mod2)
mod2.red <- lm(Yield ~ Block) # Rimozione del genotipo
SS_g <- deviance(mod2.red) - RSS
SS_g
## [1] 1.455972
mod2.red2 <- lm(Yield ~ Genotype) # Rimozione del blocco
SS_b <- deviance(mod2.red2) - RSS
SS_b
## [1] 0.1618056
# Utilizzo del metodo Anova() nel pacchetto 'car'
library(car)
Anova(mod1, type = 2)
## Anova Table (Type II tests)
##
## Response: Yield
## Sum Sq Df F value Pr(>F)
## Genotype 1.45597 3 20.5307 0.003061 **
## Block 0.16181 2 3.4224 0.115770
## Residuals 0.11819 5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova(mod2, type = 2)
## Anova Table (Type II tests)
##
## Response: Yield
## Sum Sq Df F value Pr(>F)
## Block 0.16181 2 3.4224 0.115770
## Genotype 1.45597 3 20.5307 0.003061 **
## Residuals 0.11819 5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 14.14 Conclusioni
In questo capitolo abbiamo presentato un metodo per valutare se un certo set di dati ottenuto da un esperimento controllato può ragionevolmente supportare l’esistenza di relazioni causa-effetto tra le variabili in esame.
Questo metodo consiste in:
- adattamento di un modello causa-effetto ragionevole nei dati osservati;
- utilizzo del metodo di partizionamento della varianza (ANOVA) per ottenere i quadrati medi (varianze) per tutti gli effetti causali in esame e il quadrato medio per tutti gli altri effetti di natura casuale (quadrato medio residuo);
- confronto dei quadrati medi per gli effetti causali con il quadrato medio per gli effetti casuali, utilizzando i rapporti F. Più alto è il rapporto F, più forte è la relazione causa-effetto.
Per il metodo di partizionamento della varianza con R, sono disponibili due funzioni, ‘anova()’ in base R e ‘Anova()’ nel pacchetto ‘car’. Queste due funzioni forniscono gli stessi risultati con dati bilanciati, ma la seconda è altamente consigliata quando i dati non sono bilanciati.
4.15 Altre letture
- Faraway, J.J., 2002. Practical regression and Anova using R. In: http://cran.r-project.org/doc/contrib/Faraway-PRA.pdf.
- Kuehl, R. O., 2000. Design of experiments: statistical principles of research design and analysis. Duxbury Press
4.16 Domande ed esercizi
- Qual è la differenza tra variazione congiunta e causalità?
- In valore, cosa intendiamo quando diciamo “effetto del trattamento”?
- Descrivi in poche frasi cos’è l’ANOVA e perché viene utilizzata.
- Qual è la definizione di “interazione tra due fattori sperimentali”? Spiega brevemente.
- Considera il file Excel “rimsulfuron.csv” da https://www.casaonofri.it/_datasets/rimsulfuron.csv (puoi scaricarlo o leggerlo direttamente dal repository web). Questo è un set di dati relativo a un esperimento sul campo per confrontare 14 erbicidi e due controlli non trattati, con 4 repliche per trattamento. L’esperimento è stato progettato in blocchi randomizzati. Esegui l’ANOVA con R e valuta la rilevanza dell’effetto erbicida.
- Hai eseguito un esperimento con un layout completamente randomizzato con due repliche, per confrontare due genotipi di mais (G1 e G2) con due diverse strategie di fertilizzazione (F1 e F2). Calcola i quadrati medi e i rapporti F per il genotipo, gli effetti della fertilizzazione e per la loro interazione. Gli effetti causali sono rilevanti? Il set di dati è mostrato di seguito.
| Genotype | Fertiliser | Yield |
|---|---|---|
| G1 | F1 | 11.292934 |
| G1 | F1 | 12.777429 |
| G1 | F2 | 12.584441 |
| G1 | F2 | 9.154302 |
| G2 | F1 | 14.929125 |
| G2 | F1 | 15.006056 |
| G2 | F2 | 12.925260 |
| G2 | F2 | 12.953368 |