Capitolo 14 Appendice B: Statistica descrittiva per le variabili nominali
Nel capitolo 2 abbiamo visto che le variabili qualitative sono ottenute assegnando ogni soggetto di un collettivo ad una classe scelta tra due o più possibili opzioni. Al termine di questo processo di classificazione, di solito calcoliamo le frequenza assolute, cioè il numero di individui assegnato ad ogni classe. Ad esempio, se abbiamo esaminato 500 insetti rilevando l’ordine a cui appartengono, le frequenze assolute potrebbero essere: 100 ditteri, 200 imenotteri e 150 ortotteri.
Oltre alle frequenze assolute, possiamo calcolare anche le frequenze relative, dividendo le frequenze assolute per il numero totale degli individui del collettivo. Nel caso precedentemente menzionato, la frequenza relativa dei ditteri è pari a \(100/500 = 0.2\).
Se le classi possono essere logicamente ordinate, oltre alle frequenze assolute e relative, possiamo calcolare anche le cosiddette frequenze cumulate, che si ottengono cumulando le frequenze relative di una classe con quelle di tutte le classi precedenti.
14.1 Distribuzioni di frequenze e classamento
Quando rappresentiamo, in un grafico o in una tabella, le frequenze (assolute, relative o cumulate) per tutte le classi e tutti gli individui del collettivo, otteniamo una distribuzione di frequenze.
In R, il calcolo delle frequenze assolute può essere eseguito utilizzando la funzione table(), che può essere combinata con la funzione length() (restituisce il numero di elementi in un vettore) per il calcolo delle frequenze relative e con la funzione cumsum() per le frequenze cumulate. Ad esempio, se consideriamo il famoso database ‘mtcars’, relativo alle 32 auto storiche censite dalla rivista Motor Trends nel 1974, e analizziamo il numero delle marce, otteniamo la seguente distribuzione di frequenze assolute, relative e cumulate.
abs <- table(mtcars$gear)
rel <- table(mtcars$gear)/length(mtcars$gear)
cum <- cumsum(rel)
dfr <- data.frame(
"Gears" = 3:5,
"Freq.ass" = as.numeric(abs),
"Freq.rel" = as.numeric(rel),
"Freq.cum" = as.numeric(cum))
knitr::kable(dfr, digits = 32)| Gears | Freq.ass | Freq.rel | Freq.cum |
|---|---|---|---|
| 3 | 15 | 0.46875 | 0.46875 |
| 4 | 12 | 0.37500 | 0.84375 |
| 5 | 5 | 0.15625 | 1.00000 |
Le distribuzioni di frequenze possono essere costruite anche per le variabili quantitative, tramite un’operazione di classamento, che consiste nel suddividere il campo di variazione dei dati in una serie di intervalli (esempio, da 10 a 20, da 20 a 40 e così via) e contare i soggetti in ogni classe. In questo modo, se le osservazioni sono molto numerose, la lettura delle informazioni risulta più semplice e più completa che non elencando tutti i valori o, d’altra parte, riportando solo la loro media e la loro deviazione standard.
Ad esempio, possiamo prendere 1000 numeri casuali da una distribuzione uniforme nell’intervallo da 130 a 200 ed esprimere questi mille valori tramite una distribuzione di frequenze nelle sei classi: <140, 140-150, 150-160, 160-170, 170-190, >190. Per questo compito si utilizza la funzione cut(), che con l’argomento breaks() consente di specificare gli estremi inferiori delle classi, inclusi per default nella classe successiva (intervalli aperti a sinistra e chiusi a destra). Ad esempio, se l’estremo inferiore della prima classe è 129 e quello della classe successiva è 140, i valori eventualmente inferiori o uguali a 129 sarebbero esclusi, quelli strettamente maggiori di 129 e minori o uguali a 140 sarebbero inclusi nella seconda classe.
set.seed(1234)
vals <- runif(1000, min = 130, max = 200)
freq <- table( cut(vals, breaks = c(129, 140,150,160,170,190,200)) )
freq
##
## (129,140] (140,150] (150,160] (160,170] (170,190]
## 141 140 141 141 283
## (190,200]
## 15414.2 Statistiche descrittive per le distribuzioni di frequenze
Per una distribuzione di frequenze, il più semplice indicatore di tendenza centrale è la moda, cioè il valore della classe che presenta la maggior frequenza. Ovviamente, se la variabile è quantitativa ed è stata sottoposta a classamento, si considera come moda il punto centrale della classe con maggior frequenza. L’individuazione della moda è banale e non richiede calcoli di sorta.
In alcune condizioni (distribuzioni di frequenze per caratteri qualitativi ordinabili o quantitativi sottoposti a classamento), oltre alla moda possiamo calcolare la mediana e gli altri percentili, nonché la media e le altre statistiche descrittive indicate per i caratteri quantitativi. Tuttavia, si tratta di una situazione più tipica delle scienze economiche e sociali che non delle scienze agrarie e biologiche e, per questo motivo, non la prenderemo in ulteriore considerazione.
14.3 Rappresentazione grafica delle distribuzioni di frequenza
Una distribuzione di frequenze può essere rappresentata con un grafico a torta, che, in R, può essere disegnato con ggplot, producendo un grafico a barre, con segmenti sovrapposti e ruotando il sistema di coordinate, come mostrato nel box sottostante. In questo caso il grafico è banale, in quanto le classi sono più o meno di ampiezza equivalente, dato che abbiamo utilizzato un campionamento da una distribuzione uniforme.
library(ggplot2)
dfr <- data.frame("Class" = names(freq),
"Freq" = as.numeric(freq))
ggplot(data = dfr) +
geom_bar(aes(x = NA, y = Freq, fill = Class),
stat="identity", position = "fill") +
coord_polar("y", start=0) +
theme_void() # remove background, grid, numeric labels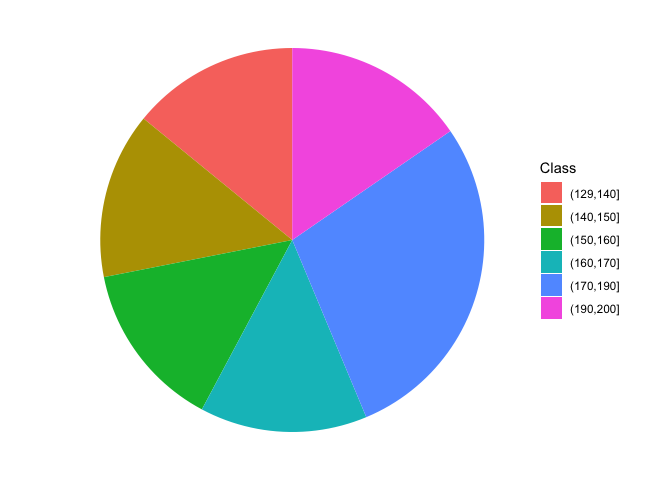
14.4 Distribuzioni di frequenza bivariate: le tabelle di contingenze
In alcuni casi, in ciascuna unità sperimentale del collettivo vengono studiati due (o più) caratteri qualitativi, che possiamo rappresentare in una tabella di contingenze. Si tratta di tabelle a due (o più) entrate, nelle quali ogni valore rappresenta la frequenza assoluta per una particolare combinazione dei caratteri rilevati.
Ad esempio, potremmo aver valutato la germinabilità di cariossidi di frumento sottoposte a due tipi di illuminazione, rossa o blu. Per ogni cariosside abbiamo quindi due informazioni, il trattamento a cui è stata sottoposta (luce rossa o blu) e se è germinata oppure no, per un totale di quattro possibili combinazioni (Rosso-si, Rosso-no, Blu-si, Blu-no). Supponendo di aver osservato 95 cariossidi germinate su 110 testate con luce rossa e 67 germinate su 120 testate con luce blu, possiamo definire la tabella di contingenze riportata di seguito.
| SI | NO | |
|---|---|---|
| ROSSO | 95 | 15 |
| BLU | 67 | 53 |
Ogni riga della tabella sovrastante costituisce una distribuzione di frequenze per la germinabilità, data una certa tipologia di luce (distribuzione di frequenze condizionate).
14.5 Connessione
Se guardiamo le due distribuzioni condizionate per la luce rossa e blu, possiamo notare che esiste una certa differenza e che la germinabilità pare maggiore con luce rossa. Potremmo chiederci quindi se una certa modalità del carattere luce (rossa o blue) influenzi il presentarsi di una particolare modalità del carattere germinabilità (si o no). Se così fosse, potremmo parlare di dipendenza o connessione, mentre, nel caso contrario, si dovrebbe parlare di indipendenza dei caratteri.
Come si fa a stabilire se i caratteri sono indipendenti o connessi? Il punto di partenza è pensare che, se i caratteri fossero indipendenti, la germinabilità dovrebbe essere la stessa con entrambi i trattamenti; in totale, abbiamo osservato 230 semi, di cui 162 sono germinati e 68 non lo sono e, di conseguenza, la proporzione di semi germinati è stata pari a 162/230 = 0.704. Ebbene, questa proporzione la si dovrebbe riscontrare con entrambi i trattamenti. In cifre, il numero di semi germinati con luce rossa dovrebbe essere pari a \(110 \times 0.704 = 77.44\), mentre il numero di semi germinati con luce blu dovrebbe essere pari a \(120 \times 0.704 = 84.48\). Rispettando i totali marginali (cioè il numero totale di semi saggiati con luce rossa e blu dovrebbe essere pari, rispettivamente a 110 e 120), possiamo costruire la tabella delle frequenze assolute attese, nell’ipotesi di indipendenza completa tra i due caratteri.
| SI | NO | |
|---|---|---|
| ROSSO | 77.44 | 32.56 |
| BLU | 84.48 | 35.52 |
A questo punto possiamo costruire un indice statistico di connessione, detto \(\chi^2\), che misuri la discrepanzatra le due tabelle, quella delle frequenze osservate e quella delle frequenze teoriche che si sarebbero dovute osservare nell’ipotesi di indipendenza perfetta:
\[\chi ^2 = \sum \left[ \frac{\left( {f_o - f_a } \right)^2 }{f_a } \right]\]
dove \(f_o\) sta per frequenza osservata ed \(f_a\) sta per frequenza attesa nel caso indipendenza. Questo indice assume valore pari a zero nel caso di indipendenza completa (le frequenze osservate sono uguali a quelle attese) ed assume un valore positivo tanto più alto quanto maggiore è la connessione tra i due caratteri.
Nel nostro esempio:
\[\chi^2 = \frac{\left( {95 - 77.44 } \right)^2 }{77.44 } + \frac{\left( {15 - 32.56 } \right)^2 }{32.56 } + \frac{\left( {67 - 84.48 } \right)^2 }{84.48 } + \frac{\left( {53 - 35.52 } \right)^2 }{35.52 } = 25.67\]
Se i caratteri fossero veramente indipendenti, la tabella delle frequenze osservate dovrebbe essere uguale a quella delle frequenze atteso, il che implicherebbe \(\chi^2 = 0\). Il valore da noi osservato è maggiore di 0 e quindi possiamo dire che esiste un certo grado di connessione, ma non sappiamo dire quanto questa sia elevata. Qual è il \(\chi^2\) massimo possibile?
Intuitivamente, possiamo immaginare che la connessione potrebbe essere la più elevata possibile quando con uno dei due trattamenti i semi sono tutti germinati, mentre con l’altro non ne è germinato nessuno, come indicato nella tabella seguente:
| SI | NO | |
|---|---|---|
| ROSSO | 110 | 0 |
| BLU | 0 | 120 |
Se calcoliamo il valore di \(\chi^2\) per la tabella sovrastante otteniamo 230, che è appunto il massimo valore possibile nella nostra condizione. Più in generale, il \(\chi^2\) massimo è dato dal prodotto del numero degli individui per il valore minimo tra il numero di righe meno una e il numero di colonne meno una:
\[\max \chi ^2 = n \cdot \min (r - 1,\,c - 1)\]
Possiamo concludere che la connessione tra i due caratteri è pari all’11% circa di quello massima (\(25.67/230 = 0.112\)).
14.6 Il chi quadro con R
Consideriamo il dataset ‘HairEyeColor’, disponibile nell’installazione di base di R e relativo al colore degli occhi e dei capelli di 520 studenti di statistica. La tabella delle contingenze, per le femmine, è la seguente:
data(HairEyeColor)
tab <- HairEyeColor[,,2]
tab
## Eye
## Hair Brown Blue Hazel Green
## Black 36 9 5 2
## Brown 66 34 29 14
## Red 16 7 7 7
## Blond 4 64 5 8Se vogliamo sapere se il colore degli occhi è legato a quello dei capelli, possiamo utilizzare la funzione as.table() per trasformare l’oggetto tab in una tabella di contingenze (in questo caso non sarebbe necessario, visto che ‘tab’ è già una tabella di contingenze) ed applicare la funzione summary(). Oltre al chi quadro, l’output fornisce anche il P-value relativo all’ipotesi nulla che non vi sia connessione tra i due caratteri.
summary(as.table (tab))
## Number of cases in table: 313
## Number of factors: 2
## Test for independence of all factors:
## Chisq = 106.66, df = 9, p-value = 7.014e-19
## Chi-squared approximation may be incorrectNell’output si legge che l’approssimazione del chi quadro potrebbe non essere corretta in quanto, quando ci sono meno di 25-30 soggetti, l’impiego di una distribuzione continua come quella di chi quadro potrebbe non essere ottimale. Nelle tabelle ‘2 x 2’ si preferisce utilizzare la funzione chisq.test(), che fornisce, per default, la correzione di Yates per la continuità. In questo caso, la stessa funzione permette di calcolare il P-value con una simulazione di Monte Carlo, evitando il problema della mancanza di continuità.
chisq.test(tab, simulate.p.value = T)
##
## Pearson's Chi-squared test with simulated
## p-value (based on 2000 replicates)
##
## data: tab
## X-squared = 106.66, df = NA, p-value = 0.000499814.7 Altre letture
- F. Crivellari (2006). Analisi statistica dei dati con R. Apogeo, Milano.
- G. Leti e L. Cerbara (2009). Elementi di statistica descrittiva. Il Mulino Editore, Bologna.
14.8 Esercizi
- Quali statistiche descrittive possono essere utilizzate con le variabili categoriche e ordinali? Illustrare brevemente e discutere
- Un ricercatore ha confrontato il rapporto tra maschi e femmine in una popolazione di insetti sottoposta a due trattamenti sperimentali diversi e si chiede se maschi e femmine manifestino una diversa sensibilità al trattamento in studio. Considerando che i maschi e le femmine osservati sono, rispettivamente 275 e 175 con il trattamento A e 326 e 297 con il trattamento B, valutare il grado di dipendenza tra i due caratteri (sesso e trattamento), in rapporto al valore minimo e massimo possibile per l’indicatore prescelto.
- Caricare il datasets ‘students’ disponibile al link: ‘https://www.casaonofri.it/_datasets/students.csv’. In questo file potete trovare una database relativo alla valutazione degli studenti in alcune materie del primo anno di Agraria. Ogni record rappresenta un esame, con il relativo voto, la materia e la scuola di provenienza dello studente. Determinare la frequenza assoluta e relativa dei diversi voti (da 18 a 30). È possibile calcolare le frequenze cumulate? Con un uso appropriato delle tabelle di contingenza e del chi quadro, valutare se il voto dipende dalla materia e dalla scuola di provenienza dello studente.