Capitolo 17 Appendice F: Alcuni problemi collegati con le deviazioni rispetti agli assunti di base

Nel codice sottostante abbiamo immaginato di campionare residui da distribuzioni normali con la stessa media, ma diverse deviazioni standard per ognuno dei quattro trattamenti sperimentali. Abbiamo quindi ottenuti 100’000 datasets nei quali l’ipotesi nulla è vera (nessuna differenza tra le medie), ma non sussiste l’omogeneità delle varianze. Sottoponendo questi datasets ad ANOVA, notiamo che la sampling distribution per F non può essere descritta con la curva di densità F di Fisher e, soprattutto, che quest’ultima funzione, nella coda destra, produce una chiara sottostima della probabilità reale e, quindi del P-value. In altre parole, quando non vi è omoscedasticità, si può incorrere in un incremento del rischio di rifiutare erroneamente l’ipotesi nulla, il che rende le nostre conclusioni molto meno attendibili.

Fvals <- c()
set.seed(1234)
Treat <- factor(rep(1:4, each = 4))
for(i in 1:100000){
  # Ysim <- rnorm(16, 14.48375, 3.9177) # Omoscedasticità
  Ysim1 <- rnorm(4, 14.48375, 0.39177)
  Ysim2 <- rnorm(4, 14.48375, 3.9177)
  Ysim3 <- rnorm(4, 14.48375, 6.9177)
  Ysim4 <- rnorm(4, 14.48375, 9.9177)
  Ysim <- c(Ysim1, Ysim2, Ysim3, Ysim4)
  mod <- lm(Ysim ~ Treat)
  Fvals[i] <- anova(mod)$F[1]
}

# b <- seq(0, 65, by=0.1)
# hist(Fvals, breaks = b, xlim = c(0, 6), freq = F,
#      xlab = "F", ylab = "Density", main = "")
# curve(df(x, 3, 12), add=T, col="blue")
knitr::include_graphics("_images/SamplingDistribF_false.png")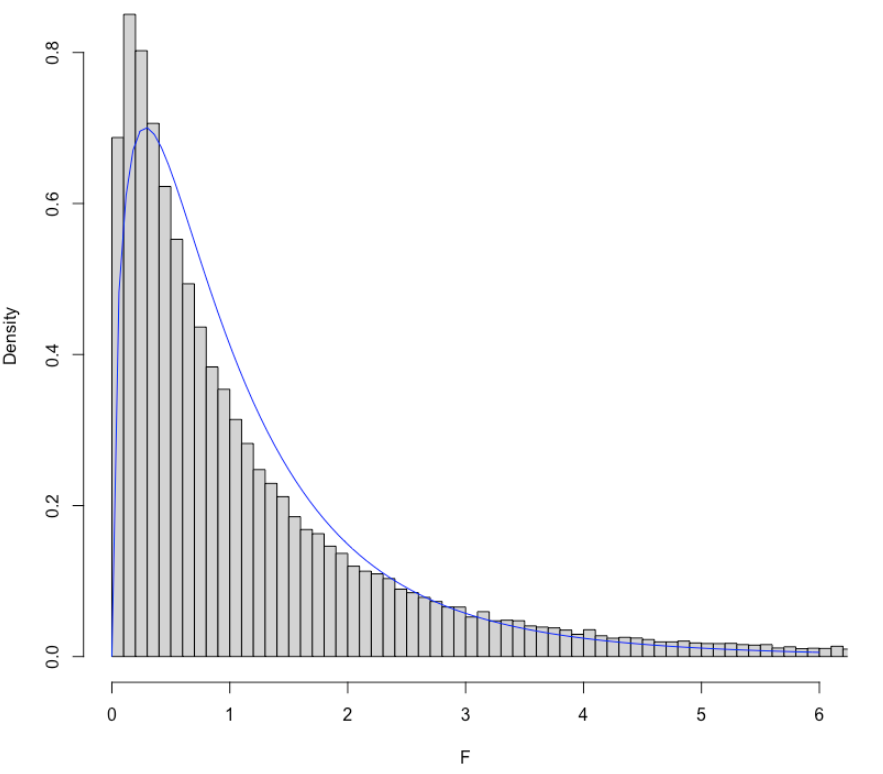

Figura 17.1: Sampling distribution empirica per F, in caso di disomogeneità delle varianze. Vediamo che, in questo caso, la funzione di densità F di Fisher non costituisce un buon riferimento per il calcolo del P-level.