Capitolo 3 Richiami di statistica descrittiva
Qualunque esperimento include un processo di raccolta dati, tramite osservazioni e/o misurazioni, al termine del quale abbiamo a disposizione un collettivo di valori, di solito organizzati sotto forma di tabella (‘dataset’), dove ogni riga corrisponde ad un’unità sperimentale (soggetto) con tutti i suoi attributi, mentre ogni colonna (detta anche variabile) corrisponde ad un attributo e contiene i valori rilevati per tutte le unità sperimentali. Un esempio delle prime righe di un dataset è riportato nella Tabella 3.1.
| Genotype | Block | Height | TKW | Whectol | Yield |
|---|---|---|---|---|---|
| arcobaleno | 1 | 90 | 44.5 | 83.2 | 64.40 |
| arcobaleno | 2 | 90 | 42.8 | 82.2 | 60.58 |
| arcobaleno | 3 | 88 | 42.7 | 83.1 | 59.42 |
| baio | 1 | 80 | 40.6 | 81.8 | 51.93 |
| baio | 2 | 75 | 42.7 | 81.3 | 51.34 |
| baio | 3 | 76 | 41.1 | 81.1 | 47.78 |
Il nostro primo compito è quello di comprendere e descrivere le caratteristiche fondamentali di ogni variabile, utilizzando statistiche descrittive opportunamente scelte, in base al tipo di dato e alle caratteristiche che si vogliono descrivere.
3.1 Descrizione di dati quantitativi
Se i dati sono stati ottenuti con un processo di misurazione e rappresentano una quantità, come, ad esempio, il peso, l’altezza, la concentrazione e così via, abbiamo una variabile quantitativa, della quale dobbiamo descrivere almeno due caratteristiche fondamentali:
- tendenza centrale
- dispersione
La tendenza centrale è un valore che rappresenta il ‘centro’, attorno al quale si collocano tutte le osservazioni; al contrario, la dispersione misura la distanza delle osservazioni tra di loro, cioè, in altre parole, la loro variabilità. Ovviamente, esistono anche altre importanti proprietà di una variabile quantitativa, come la simmetria e la curtosi, che, tuttavia, non verranno prese in considerazione in questo libro, rimandando alla lettura di testi più approfonditi (Sokal e Rohlf, 1981; Leti e Cerbara, 2009).
Un altro aspetto che è necessario precisare è che, almeno nella sperimentazione agraria, non è infrequente rilevare, in ogni parcella, alcune variabili nominali, come la presenza di individui infetti la presenza/assenza di piante infestanti oppure alcune variabili discrete, frutto di conteggio, ad esempio il numero di piante infestanti o la fittezza della coltura e così via. Nonostante esistano metodi specifici per variabili nominali e discrete, è comune trasformare le variabili nominali in forma di frequenze relative (ad esempio, il numero di piante infette sul totale campionato) per ogni parcella, che sono poi trattate alla stregua delle variabili quantitative, così come i conteggi per parcella.
3.1.1 Indicatori di tendenza centrale
L’indicatore di tendenza centrale più diffuso è la media aritmetica, che non necessita di particolari spiegazioni: si tratta della somma dei dati (\(x\)) divisa per il loro numero (\(n\)):
\[\mu = \frac{\sum\limits_{i = 1}^n x}{n}\]
Per esempio, consideriamo il seguente dataset, che elenca le altezze di quattro piante di mais \(d = [178, 175, 158, 153]\)
Il calcolo della media è banale:
\[\mu = \frac{178 + 175 + 158 + 153}{4} = 166\]
La media è ‘centrale’ nel senso che la somma delle sue distanze da ogni altra osservazione è nulla. Di conseguenza, è molto sensibile ai valori estremi; se, ad esempio, supponiamo di avere i cinque valori: 1, 4, 7, 9 e 10 con media pari a 6,2 e supponiamo di sostituire il valore più alto con 100, la media aumenta di conseguenza, diventando pari a 24,2. Per questa sua sensibilità ai valori estremi, si dice che la media non è un indicatore di tendenza centrale ‘robusto’ nei confronti degli outliers, cioè delle osservazioni in qualche modo ‘aberranti’. In presenza di queste osservazioni, che potrebbero essere frutto di un errore sperimentale rilevante, la media tende a non rappresentare più la tendenza centrale del collettivo in modo affidabile.
Un altro indicatore di tendenza centrale è la mediana, cioè il valore che bipartisce i dati in modo che la metà di essi siano più alti e la metà più bassi. Per calcolare la mediana, basta ordinare i soggetti in ordine crescente: se il numero di individui è dispari, la mediana è data dal valore dall’individuo che occupa il posto centrale o, se gli individui sono in numero pari, dalla media delle due osservazioni centrali. Nell’esempio precedente, i dati sono in numero pari, quindi la mediana è: \((158 + 175)/2 = 166.5\).
La mediana è un indicatore più robusto della media: infatti, se consideriamo gli stessi cinque valori elencati in precedenza (1, 4, 7, 9 e 10), la mediana è pari a 7 e non cambia quando sostituiamo il valore più alto con 100.
3.1.2 Indicatori di dispersione
Conoscere la tendenza centrale di un collettivo è importante, ma non è sufficiente. Infatti, una media pari a 100 può essere ottenuta con tre individui che misurano 99, 100 e 101, rispettivamente, o con tre individui che misurano 1, 100 e 199. E’ evidente che i due gruppi hanno la stessa tendenza centrale, ma sono molto diversi in termini di dispersione (o variabilità) rispetto alla media. Per descrivere la dispersione dei dati possiamo utilizzare il campo di variazione, che è la differenza tra la misura più bassa e la misura più alta. In realtà, questo indicatore è poco diffuso, perché considera solo i valori estremi del collettivo e non necessariamente cresce al crescere della variabilità. Altri indicatori sono più diffusi ed affidabili, come la devianza, la varianza, la deviazione standard ed il coefficiente di variabilità, tutti legati da relazioni algebriche ben definite.
La devianza, generalmente nota come somma dei quadrati (abbreviata SS, da sum of squares) è data da:
\[SS = \sum\limits_{i = 1}^n {(x_i - \mu)^2 }\]
Ad esempio, per le quattro altezze menzionate in precedenza, la devianza è pari a:
\[SS = \left(178 - 166 \right)^2 + \left(175 - 166 \right)^2 + \left(158 - 166 \right)^2 + \left(153 - 166 \right)^2 = 458\]
La devianza è un indicatore di dispersione molto utilizzato, soprattutto perché ha un suo preciso significato geometrico, in quanto somma delle distanze euclidee al quadrato, rispetto alla media. Tuttavia, ha due aspetti che vanno tenuti in considerazione: in primo luogo, proprio perché è una somma, il valore finale dipende dal numero di addendi e quindi non la si può utilizzare per confrontare la variabilità di collettivi con diversa numerosità. Inoltre, l’unità di misura della devianza è pari al quadrato dell’unità di misura originale dei dati; ad esempio se le osservazioni sono espresse in centimetri (come nel nostro esempio), la devianza è espressa in centimetri quadrati, il che rende più difficoltosa l’interpretazione dei risultati.
Oltre dalla devianza, un indicatore molto utilizzato è la varianza campionaria (o semplicemente varianza), che è data dalla devianza divisa per il numero di dati meno uno:
\[\sigma^2 = \frac{SS}{n - 1}\]
Nel caso delle nostre altezze:
\[\sigma^2 = \frac{458}{3} = 152.67\]
La varianza è anche detta scarto quadratico medio è permette di confrontare la variabilità di collettivi diversamente numerosi, anche se permane il problema dell’unità di misura, che è sempre il quadrato di quella delle singole osservazioni. Per eliminare questo problema si ricorre alla radice quadrata della varianza, cioè la deviazione standard, che si indica con \(\sigma\). La deviazione standard è espressa nella stessa unità di misura dei dati originali ed è quindi molto utilizzata per descrivere l’incertezza assoluta di misure ripetute più volte. Nel nostro caso, risulta che:
\[\sigma = \sqrt{152.67} = 12.36\]
e questo valore ci fa capire che, ‘mediamente’, la distanza euclidea tra ogni valore e \(\mu\) è pari \(12.36\) centimetri. Media e deviazione standard sono spesso riportate contemporaneamente, utilizzando un intervallo \(l\) definito come:
\[l = \mu \pm \sigma\]
Un problema della deviazione standard è che essa, in assenza della media, non riesce a dare informazioni facilmente comprensibili; infatti, se dicessimo semplicemente che un gruppo di individui ha una deviazione standard pari a \(12.36\), cosa potremmo concludere in relazione alla variabilità di questo collettivo? È alta o bassa? È evidente che, senza sapere la media, non riusciamo a rispondere a questa domanda: la variabilità potrebbe essere considerata molto alta se la media fosse bassa (ad esempio 16), oppure molto bassa, se la media fosse alta (esempio 1600). Per questo, se dovessimo descrivere la variabilità dei dati indipendentemente dalla media, dovremmo utilizzare il coefficiente di variabilità (CV):
\[CV = \frac{\sigma }{\mu } \times 100\]
Il CV è un numero puro e non dipende dall’unità di misura e dall’ampiezza del collettivo, sicché è molto adatto ad esprimere, ad esempio, l’errore degli strumenti di misura e delle apparecchiature di analisi (incertezza relativa). Nel nostro caso, abbiamo:
\[CV = \frac{12.36}{166} \times 100 = 7.45 \%\]
Come la media, anche la devianza, la varianza e la deviazione standard sono sensibili agli outliers. Pertanto, in presenza di osservazioni aberranti, preferiamo descrivere la variabilità del collettivo utilizzando i cosiddetti percentili, che, estendendo il concetto di mediana, bipartiscono il collettivo in modo da lasciare una certa percentuale di individui alla loro sinistra. Ad esempio, il primo percentile bipartisce il collettivo in modo che l’1% dei soggetti sono più bassi e il 99% sono più alti. Allo stesso modo, l’ottantesimo percentile bipartisce il collettivo in modo che l’80% dei soggetti sono più bassi e il 20% sono più alti. Ovviamente, la mediana rappresenta il 50-esimo percentile.
I percentili più utilizzati per descrivere la dispersione di un collettivo sono il 25-esimo e il 75-esimo, che individuano un intervallo all’interno del quale è compreso il 50% dei soggetti: se questo intervallo è piccolo, significa che la variabilità è bassa. Calcolare i percentili a mano non è banale e, di conseguenza, lo faremo nei paragrafi successivi, utilizzando R.
3.1.3 Incertezza delle misure derivate
A volte noi misuriamo due quantità e poi le combiniamo, per ottenere una misura derivata, ad esempio la somma o la differenza. Se le due misure hanno un certo grado di incertezza, quantificabile, ad esempio, con la deviazione standard, qual è l’incertezza della loro somma o della loro differenza? La legge di propagazione degli errori dice che, in caso di misure indipendenti, la deviazione standard di una somma o di una differenza è uguale alla radice quadrata della somma dei quadrati delle deviazioni standard degli addendi. Ad esempio, se abbiamo fatto due misure indipendenti in triplicato, ottenendo le due medie \(22\) e \(14\), con deviazioni standard rispettivamente pari a \(2\) e \(3\), la somma sarà pari a \(36\), con deviazione standard pari \(\sqrt{2^2 + 3^2} = 3.6\), mentre la differenza sarà pari ad \(8\) con deviazione standard comunque pari a \(3.6\). Ovviamente è anche possibile calcolare la deviazione standard di misure derivate con funzioni diverse dalla somma o dalla differenza, ma si tratta di una situazione meno comune, che non tratteremo in questo libro.
3.1.4 Relazioni tra variabili quantitative: correlazione
Se su ogni soggetto abbiamo rilevato due caratteri quantitativi (ad esempio il peso e l’altezza, oppure la produzione e il contenuto di proteina della granella), è possibile verificare se esista una relazione tra la coppia di variabili ottenute, cioè se al variare di una cambi anche il valore dell’altra, in modo congiunto (variazione congiunta).
Per questo fine, si utilizza il coefficiente di correlazione di Pearson costituito dal rapporto tra la codevianza (o somma dei prodotti) delle due variabili e la radice quadrata del prodotto delle loro devianze. Vedremo tra poco il metodo di calcolo, ma vogliamo anticipare che il coefficiente di correlazione varia tra \(-1\) e \(+1\); se è pari ad 1, abbiamo una situazione ideale di concordanza perfetta (quando aumenta una variabile, aumenta anche l’altra in modo esattamente proporzionale), mentre quando è pari a \(-1\), abbiamo una situazione ideale di discordanza perfetta (quando aumenta una variabile, diminuisce l’altra in modo inversamente proporzionale). Un valore pari a \(0\) è altrettanto ideal ed indica assenza di qualunque grado di variazione congiunta (assenza di correlazione). Nell’intervallo tra \(-1\) ed \(1\), il coefficiente indica una correlazione imperfetta, ma tanto migliore quanto più ci allontaniamo dallo zero e ci avviciniamo a \(-1\) o \(1\). Due esempi di ottima correlazione sono mostrati in Figura 3.1; si evidenzia un elevato grado di correlazione, che, tuttavia, non è perfetta, in quanto i punti non sono esattamente allineati.
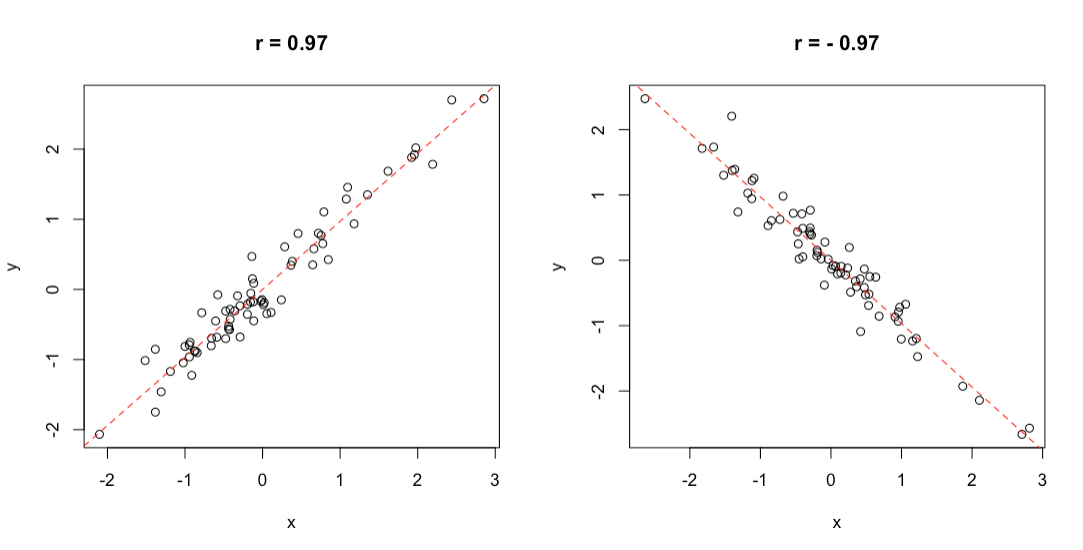
Figura 3.1: Esempio di correlazione positiva (destra) e negativa (sinistra)
Proviamo a considerare questo esempio: il contenuto di olio di 9 lotti di acheni di girasole è stato misurato con due metodi diversi ed è riportato più sotto.
A <- c(45, 47, 49, 51, 44, 37, 48, 44, 53)
B <- c(44, 44, 49, 53, 48, 34, 47, 46, 51)Per valutare la entità della correlazione tra i risultati dei due metodi di analisi, dobbiamo eseguire alcune operazioni preliminari, cioè:
- calcolare i residui per A (\(z_A\))
- calcolare i residui per B (\(z_B\))
- calcolare devianze e codevianze
In primo luogo, calcoliamo le due medie, che sono, rispettivamente, 46.44 e 46.22. Successivamente, possiamo calcolare i residui, come differenze tra ogni dato e la sua media, i loro quadrati ed i loro prodotti, come indicato in Tabella 3.2.
| A | B | \(z_A\) | \(z_B\) | \(z_A \times z_B\) | \(z_A^2\) | \(z_B^2\) |
|---|---|---|---|---|---|---|
| 45 | 44 | -1.444 | -2.222 | 3.210 | 2.086 | 4.938 |
| 47 | 44 | 0.556 | -2.222 | -1.235 | 0.309 | 4.938 |
| 49 | 49 | 2.556 | 2.778 | 7.099 | 6.531 | 7.716 |
| 51 | 53 | 4.556 | 6.778 | 30.877 | 20.753 | 45.938 |
| 44 | 48 | -2.444 | 1.778 | -4.346 | 5.975 | 3.160 |
| 37 | 34 | -9.444 | -12.222 | 115.432 | 89.198 | 149.383 |
| 48 | 47 | 1.556 | 0.778 | 1.210 | 2.420 | 0.605 |
| 44 | 46 | -2.444 | -0.222 | 0.543 | 5.975 | 0.049 |
| 53 | 51 | 6.556 | 4.778 | 31.321 | 42.975 | 22.827 |
La somma dei quadrati dei residui ci permette di calcolare le devianze di \(A\) e \(B\) (rispettivamente 176.22 e 239.56), mentre la somme dei prodotti degli residui ci permette di calcolare la codevianza (pari a 184.11).
Il coefficiente di correlazione è quindi:
\[r = \frac{184.11}{\sqrt{176.22 \times 239.56}} = 0.896\]
Vediamo che il coefficiente di correlazione è abbastanza vicino ad 1 e quindi possiamo concludere che i due metodi di analisi danno risultati ben concordanti.
3.2 Statistiche descrittive con R
Le statistiche descrittive si calcolano facilmente con R. Per esercizio, utilizziamo il dataset ‘heights.csv’, che è disponibile in una repository online. Il box sottostante mostra come caricare il dataset, del quale utilizzeremo la colonna ‘height’ che riporta le altezze di venti piante di mais.
filePath <- "https://www.casaonofri.it/_datasets/heights.csv"
dataset <- read.csv(filePath, header = T)
dataset$height
## [1] 172 154 150 188 162 145 157 178 175 158 153 191 174 141 165 163
## [17] 148 152 169 185La media si calcola con la funzione mean(), mentre la mediana si calcola con la funzione median().
mean(dataset$height)
## [1] 164
median(dataset$height)
## [1] 162.5Per la devianza, non esiste una funzione dedicata e dobbiamo utilizzare l’equazione fornita in precedenza:
sum( (dataset$height - mean(dataset$height))^2 )
## [1] 4050Varianza e deviazione standard sono molto facili da calcolare, grazie alle funzioni apposite, mentre il coefficiente di variabilità si può calcolare con la formula fornita in precedenza:
var(dataset$height)
## [1] 213.1579
sd(dataset$height)
## [1] 14.59993
sd(dataset$height)/mean(dataset$height) * 100
## [1] 8.902395Per calcolare i percentili si usa la funzione quantile(), fornendo le proporzioni di soggetti da lasciare sulla sinistra con l’argomento ‘probs’. Ad esempio, per il 25-esimo percentile utilizzeremo 0.25, mentre per il 75-esimo utilizzeremo 0.75:
quantile(dataset$height, probs = c(0.25, 0.75))
## 25% 75%
## 152.75 174.25La correlazione si calcola invece con la funzione cor(), come indicato più sotto.
cor(A, B)
## [1] 0.89607953.2.1 Descrizione dei sottogruppi
In biometria è molto comune che il gruppo di soggetti sia divisibile in più sottogruppi, corrispondenti, ad esempio, ai diversi trattamenti sperimentali. In questa comune situazione siamo soliti calcolare, per ogni gruppo, le statistiche descrittive già viste in precedenza, utilizzando la funzione tapply() in R, come mostrata più sotto.
m <- tapply(dataset$height, dataset$var, mean)
s <- tapply(dataset$height, dataset$var, sd)
descript <- data.frame(Media = m, SD = s)
descript
## Media SD
## C 165.00 14.36431
## N 164.00 16.19877
## S 160.00 12.16553
## V 165.25 19.51709Nel codice immediatamente precedente, height è la variabile che contiene i valori da mediare, var è la variabile che contiene la codifica di gruppo, mean è la funzione che dobbiamo calcolare. Ovviamente mean può essere sostituito da qualunque altra funzione ammissibile in R, come ad esempio la deviazione standard. Nel codice precedente abbiamo utilizzato la funzione data.frame() per creare una tabella riassuntiva con le medie e le deviazioni standard dei quattro gruppi.
Oltre che in una tabella, i risultati possono anche essere riportati in un grafico a barre, con l’indicazione della variabilità dei dati. Possiamo utilizzare la funzione barplot() alla quale passeremo come argomenti l’altezza delle barre, data dalle medie dei diversi gruppi, i nomi dei gruppi medesimi e, opzionalmente, la scala dell’asse delle ordinate. La funzione barplot(), oltre che creare il grafico, restituisce le ascisse del centro di ogni barra, che possiamo utilizzare per creare dei segmenti verticali corrispondenti alle deviazioni standard di ogni gruppo, attraverso la funzione arrows().
L’uso di quest’ultima funzione non è immediato; poniamo che le ascisse del centro di ogni barra siano contenute nel vettore ‘coord’; allora i segmenti di variabilità dovranno avere punti di partenza con ascisse contenute in ‘coord’ ed ordinate uguali all’altezza di ogni barra meno la deviazione standard. I punti di arrivo, invece, dovranno avere le stesse ascisse dei punti di partenza ed ordinate uguali all’altezza di ogni barra più la deviazione standard. Gli altri argomenti della funzione arrows() servono per meglio specificare l’aspetto dei segmenti di variabilità; ad esempio, il codice sottostante produce il risultato mostrato in Figura 3.2; il grafico non è bellissimo, ma, con un po’ di esercizio, è possibile ottenere grafici altamente professionali.
coord <- barplot(descript$Media, names.arg = row.names(descript),
ylim = c(0, 200))
arrows(coord, descript$Media - descript$SD,
coord, descript$Media + descript$SD,
length = 0.05, angle = 90, code = 3)
Figura 3.2: Esempio di boxplot in R
Quando abbiamo a che fare con gruppi molto numerosi, con un certo numero di outliers, è bene sostituire la mediana alla media, in associazione con il 25-esimo e 75-esimo percentile, come indicazioni di variabilità. Da un punto di vista grafico, possiamo utilizzare un boxplot (grafico Box-Whisker). Si tratta di una scatola (box) che ha per estremi il 25-esimo e il 75-esimo percentile ed è tagliata da una linea centrale in corrispondenza della mediana. Dalla scatola partono due linee verticali (baffi = whiskers) che identificano il valore massimo e il minimo. Se il massimo (o il minimo) distano dalla mediana più di 1.5 volte la differenza tra la mediana stessa e il 75-esimo (o 25-esimo) percentile, allora le linee verticali si fermano ad un valore pari ad 1.5 volte il 75-esimo (o il 25-esimo) percentile ed i dati più estremi vengono considerati outliers e rappresentati con un piccolo cerchio. In Figura 3.3 abbiamo raprresentato tre gruppi di valori estratti casualmente nell’intervallo da 0 ad 1.
set.seed(1234)
A <- runif(20)
B <- runif(20)
C <- runif(20)
series <- rep(c("A", "B", "C"), each = 20)
values <- c(A, B, C)
boxplot(values ~ series)
Figura 3.3: Esempio di boxplot in R
3.3 Altre letture
- F. Crivellari (2006). Analisi statistica dei dati con R. Apogeo, Milano.
- G. Leti and L. Cerbara (2009). Elementi di statistica descrittiva. Il Mulino Editore, Bologna.
- R.R Sokal and Rohlf, F.J. (1981). Biometry. W.H. Freeman and Company, Books.
3.4 Domande ed esercizi
- Illustrare e discutere i principali indici di tendenza centrale per le variabili quantitative
- Illustrare e discutere i principali indici di variabilità per le variabili quantitative
- Illustrare e discutere il coefficiente di correlazione di Pearson
- Un’analisi chimica è stata eseguita in triplicato e i risultati sono stati i seguenti: 125, 169 and 142 ng/g. Calcolate la media e tutti gli indicatori di variabilità che conoscete. In che modo può essere espressa l’incertezza assoluta della misura?
- Un ricercatore ha misurato l’altezza di quattro alberi ed il loro diametro (entrambi in metri). I risultati ottenuti sono i seguenti:
Altezza <- c(2.3, 2.7, 3.1, 3.5)eDiametro <- c(0.46, 0.51, 0.59, 0.64). Calcolare il coefficiente di correlazione di Pearson e valutare l’entità della correlazione in base ai valori massimi e minimi ammissibili per questa statistica. - Considerate il file EXCEL ‘rimsulfuron.csv’, che potete trovare in questo percorso: https://www.casaonofri.it/_datasets/rimsulfuron.csv. In questo file sono riportati i risultati di un esperimento con 16 trattamenti e 4 repliche, nel quale sono stati posti a confronti diversi erbicidi e/o dosi per il diserbo nel mais. Calcolare le medie produttive ottenute con le diverse tesi sperimentali e riportarle su un grafico, includendo anche un’indicazione di variabilità. Verificare se la produzione è correlata con il ricoprimento (WeedCover) delle piante infestanti.