Capitolo 6 Stime ed incertezza

Abbiamo visto che:

i fenomeni biologici seguono una legge di natura (verità ‘vera’), che ne costituisce il meccanismo deterministico fondamentale. A livello di popolazione, questa legge di natura produce un risultato atteso (media) \(Y_E\).
Quando si organizza un esperimento, i soggetti sperimentali obbediscono a questo meccanismo di fondo, al quale tuttavia si sovrappongono molto altri elementi di ‘confusione’, altamente incontrollabili, che vanno sotto il nome di errore sperimentale. Il più importante ed inevitabile elemento di confusione è il fatto che il campione prescelto, anche se rappresentativo non riflette mai esattamente le caratteristiche della popolazione da cui proviene (sampling error).
L’osservazione sperimentale è quindi un’immagine confusa della verità vera (\(Y_O \neq Y_E\)) e, soprattutto, essa tende ad essere sempre diversa, anche quando ripetiamo lo stesso esperimento nelle stesse condizioni.

Come facciamo, quindi, a gestire questa fondamentale ‘irriproducibilità’ dei risultati? E, soprattutto, come facciamo a dare informazioni sulla ‘verità vera’ quando ne conosciamo soltanto una ‘copia sbiadita’ (Fig. 6.1)? Usualmente ci serviamo di un processo che prende il nome di inferenza statistica ed è basato sulle teorie di Karl Pearson (1857-1936), di suo figlio Egon Pearson (1895-1980), di Jarzy Neyman (1894-1981), in aggiunta al contributo di Ronald Fisher, del quale abbiamo già detto in precedenza.

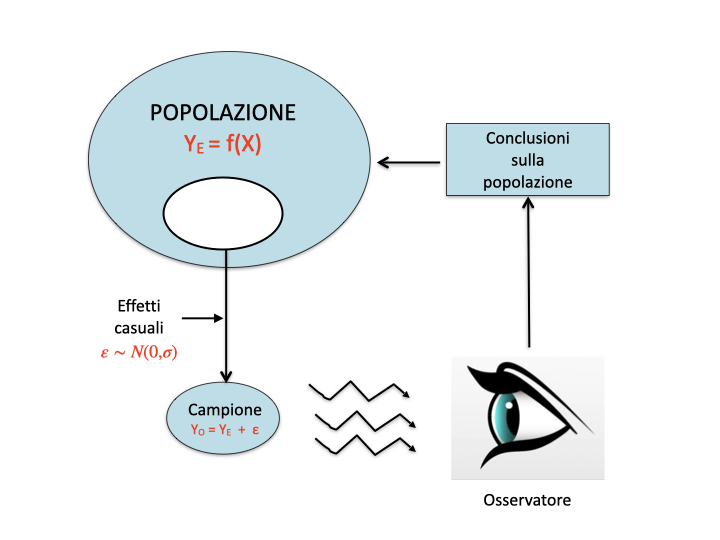
Figura 6.1: Osservazioni sperimentali e meccanismi perturbativi

Riprendiamo l’esempio relativo ad un pozzo inquinato da un erbicida a concentrazione pari a 120 \(mg/L\) (Capitolo 5), misurata tramite uno strumento che, unitamente a tutte le altre fonti ignote di errore, produce un coefficiente di variabilità del 10% (corrispondente ad una deviazione standard di 12 \(mg/L\)). Abbiamo visto che, immaginando di fare le analisi in triplicato, i risultati di questo esperimento possono essere simulati con il modello della media, come lo abbiamo descritto nel capitolo precedente, cioè \(Y_O = Y_E + \varepsilon\), con \(\varepsilon \sim N(0, \sigma)\), \(Y_E = 120\) e \(\sigma = 12\).

Nell’esempio 5.3, la simulazione di Monte Carlo ha portato ai seguenti risultati: 105,5, 123,3 e 133,01 mg/L. Se adattiamo il “modello della media” a questo set di dati otteniamo un valore \(m = 120.62\), che differisce, anche se di poco, dal valore vero \(\mu = 120\). C’è quindi una discrasia tra la statistica campionaria e quella della popolazione (\(m \neq \mu\)).

set.seed(1234)
Y_E <- 120
epsilon <- rnorm(3, 0, 12)
Y_O <- Y_E + epsilon

# Fitting the ’model of the mean’ to the observed results
mod <- lm(Y_O ~ 1)
coef(mod)
## (Intercept) 
##    120.6192

A questo punto rimettiamoci in una situazione reale: non sappiamo quale sia la concentrazione nel pozzo e cerchiamo di determinarla utilizzando i risultati dell’esperimento appena citato. In assenza di altre informazioni, è logico concludere che \(\mu = m\), cioè che la statistica della popolazione coincida con quella campionaria. Questo processo con il quale assegniamo alla popolazione il valore della statistica campionaria prende il nome di stima puntuale. È un processo legittimo, ma insufficiente, in quanto \(m \neq \mu\), il che non ci sorprende: non è ragionevole infatti pensare che un qualunque campione possa riflettere con esattezza le caratteristiche della popolazione che lo ha generato. La nostra stima dovrà quindi essere ben più prudenziale.

L’approccio tradizionale consiste nel determinare un un intervallo di valori, che sia in grado di “catturare” la statistica della popolazione con elevata confidenza e una bassa probabilità di errore (stima per intervallo). Tale intervallo è chiamato Intervallo di confidenza (Confidence Interval: CI) ed è basato sulle teorie di Karl Pearson (1857-1936), di suo figlio Egon Pearson (1895-1980) e di Jerzy Neyman (1894-1981), nonché sul lavoro di Ronald Fisher. Il CI è uno dei fondamenti della cosiddetta inferenza frequentista, che non è l’unico tipo di inferenza disponibile e non è esente da alcune incongruenze concettuali (vedi Morey et al., 2016). Tuttavia, è molto comune e ampiamente utilizzata nella maggior parte degli articoli scientifici. Il termine “frequentista” deriva dal fatto che l’IC è costruito considerando la variabilità delle stime campionarie quando gli esperimenti vengono ripetuti e la frequenza con cui vengono ottenute i valori ‘sbagliati’.

6.1 Ripetere gli esperimenti

Il nostro esperimento è solo simulato e possiamo quindi ripeterlo ‘gratuitamente’ un numero anche molto elevato di volte, seguendo questa procedura:

Ripetiamo l’estrazione precedente per 100’000 volte (in altre parole: immaginiamo di ripetere l’analisi chimica per 100’000 volte, sempre con tre repliche)
Otteniamo 100’000 medie
Calcoliamo la media delle medie e la deviazione standard delle medie

# Code box 6.2

# Monte Carlo simulation #1
nrep <- 3
mean <- 120
sigma <- 12
set.seed(1234)
result <- rep(0, 100000)
for (i in 1:100000){
  sample <- rnorm(nrep, mean, sigma)
  mod <- lm(sample ~ 1)
  result[i] <- coef(mod)
}

# Characterising the population of estimates
min(result)

## [1] 90.14123

max(result)

## [1] 149.0346

result[result == 120]

## numeric(0)

mean(result)

## [1] 120.0341

sd(result)

## [1] 6.939063

Alla fine del processo ci troviamo con una popolazione di medie, che viene detta distribuzione campionaria (sampling distribution); si tratta di un ‘oggetto’ abbastanza ‘teorico’, ma fondamentale per la statistica frequentista, perché caratterizza la variabilità dei risultati di un esperimento, e quindi la sua riproducibilità.

Notiamo che:

La media delle medie è praticamente coincidente con \(\mu\), la verità ‘vera’. Ciò conferma che la stima puntuale \(m\) è uno stimatore non distorto di \(\mu\), perché tende a convergere su \(\mu\) quando il numero di repliche tende a diventare molto elevato;
La deviazione standard delle medie è pari a 6.939063 e prende il nome di errore standard (SE).

Quest’ultima statistica è di importanza fondamentale, in quanto caratterizza la replicabilità di un esperimento, ovvero la sua precisione. Più è alto l’errore standard, più è incerta la stima e più è alta la sua variabilità in caso di esperimenti ripetuti.

Inoltre, possiamo osservare che il 2.5° e il 97.5° percentile sono, rispettivamente:

quantile(result, probs =c(0.025, 0.975))
##     2.5%    97.5% 
## 106.4884 133.6434

Possiamo quindi dire che, ripetendo un esperimento un numero elevatissimo di volte, il 95% dei risultati sono contenuti in un intervallo ben definito, che comprende al suo interno il valore ‘vero’ della statistica da stimare.

6.2 La ‘sampling distribution’ teorica

La sampling distribution definita più sopra è puramente empirica e sarebbe molto utile poterla descrivere con una funzione di densità formale. Se discretizziamo il vettore ‘result’ e riportiamo le frequenze su un grafico a barre (Fig. 6.2 ), vediamo con chiarezza che la sampling distribution empirica somiglia molto ad una distribuzione normale, con media pari a 120 e deviazione standard pari a 6.94.

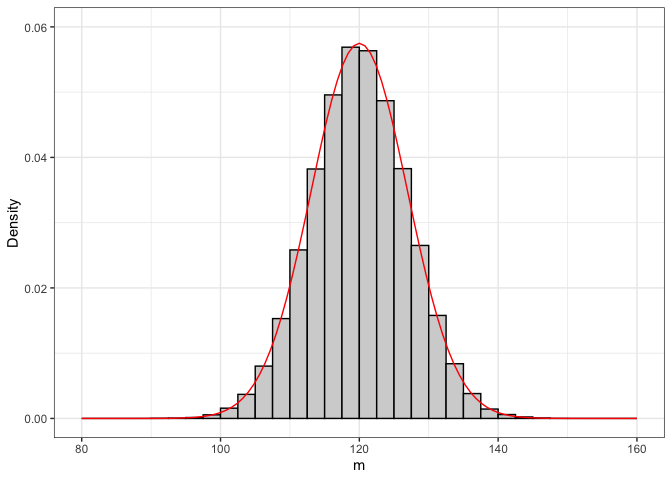
Empirical distribution of 100,000 sample estimates (n = 3), drawn from a Gaussian population with mean = 120 and SD = 12. The solid line shows the theoretical Gaussian PDF, with mean = 120 and SD = 6.94

Figura 6.2: Empirical distribution of 100,000 sample estimates (n = 3), drawn from a Gaussian population with mean = 120 and SD = 12. The solid line shows the theoretical Gaussian PDF, with mean = 120 and SD = 6.94

Questa somiglianza può essere spiegato in base al teorema centrale del limite (o teorema del limite centrale), che teorizza che, qualunque sia la popolazione di partenza, molte statistiche campionarie, tra cui la media, calcolate su campioni casuali ed indipendenti, tendono a distribuirsi in modo approssimativamente normale, con una media pari alla corrispondente statistica della popolazione¹.

Ammettendo che la sampling distribution fosse Gaussiana, l’intervallo di cui abbiamo parlato poco sopra potrebbe essere individuato facilmente considerando un multiplo dell’errore standard, come \(\mu - k \times SE\) e \(\mu + k \times SE\) (Fig. 6.3). Inoltre, \(k\) sarebbe pari al 97.5° percentile di una distribuzione gaussiana standardizzata (ovvero una distribuzione gaussiana con media uguale a 0 e deviazione standard pari a 1), che è prossimo a 2 (con R: qnorm(0,975) = 1.960). Sfortunatamente, nella maggior parte dei casi, la distribuzione campionaria è solo approssimativamente gaussiana, quindi \(k\) deve essere determinato in modo diverso, come vedremo in seguito.

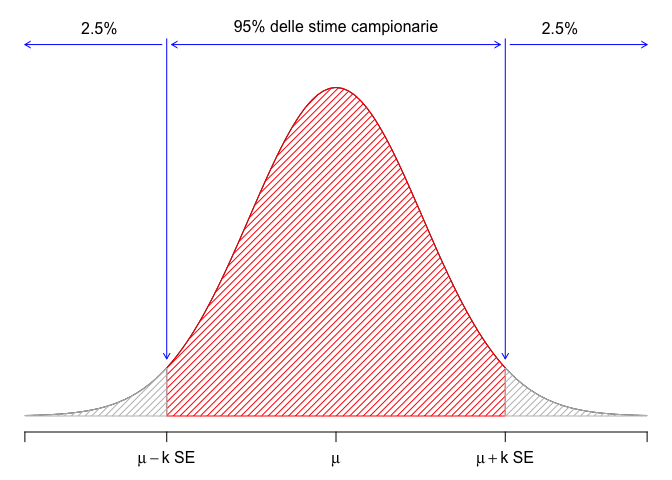
A gaussian sampling distribution with a mean of 120 and standard deviation equal to 6.94 (n = 3); the red interval contains 95% of our sample means and it is obtained by adding/subtracting to/from 120 a value equal to, approximately, twice the standard error

Figura 6.3: A gaussian sampling distribution with a mean of 120 and standard deviation equal to 6.94 (n = 3); the red interval contains 95% of our sample means and it is obtained by adding/subtracting to/from 120 a value equal to, approximately, twice the standard error

6.3 L’intervallo di confidenza frequentista

Come abbiamo detto, l’intervallo menzionato in precedenza contiene il 95% delle stime campionarie e, di conseguenza, soddisfa la seguente espressione:

\[P \left[ \mu - k \times SE \leq m \leq \mu + k \times SE \right] = 0.95\]

Con semplici passaggi algebrici (sottraiamo \(\mu\) ed \(m\) da tutti i termini, moltiplichiamo per \(-1\) e riorganizziamo l’espressione), possiamo ricavare la seguente:

\[P \left[ m - k \times SE \leq \mu \leq m + k \times SE \right] = 0.95\]

che è di estrema importanza, in quanto esprime il concetto che, se facciamo un esperimento ed otteniamo una media pari ad \(m\) e scegliamo accuratamente \(k\), possiamo costruire un intervallo di confidenza intorno alla nostra stima, pari a \(k\) volte l’errore standard e tale da contenere la media vera \(\mu\) con una probabilità del 95%. Questa espressione costituisce l’euristica più utilizzata per costruire l’intervallo di confidenza, anche se dobbiamo capire come ottenere SE e k.

6.4 Come otteniamo l’errore standard?

In alcuni casi, l’errore standard può essere ottenuto tramite semplici regole (Cochran, 1950), a partire dalla deviazione standard della popolazione di partenza. Ad esempio, nel caso della media campionaria, l’errore standard (SEM: Standard Error of a Mean) può essere ottenuto con la legge di propagazione degli errori (vedi capitolo 3.3):

\[\textrm{SEM} = \frac{\sigma}{\sqrt n}\]

Nell’esempio precedente, l’errore standard è \(12/\sqrt{3} = 6,928\), molto vicino alla deviazione standard della distribuzione campionaria empirica.

Allo stesso modo, è possibile dimostrare che l’errore standard della differenza tra le medie di due campioni (SED: Standard Error of a Difference) indipendenti con numerosità, rispettivamente, pari a \(n_1\) ed \(n_2\), estratti da due popolazioni con la stessa varianza e la stessa media è:

\[\textrm{SED} = \sqrt{ \frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}}\]

A parte questi due semplici casi, calcolare manualmente l’errore standard è difficile, ma, fortunatamente, possiamo utilizzare quelli prodotti dal software statistico in nostra vece. In particolare, per i modelli ottenuti con la funzione lm() o con altre funzioni di fitting in R, gli errori standard per le stime dei parametri possono essere ricavati con la funzione summary(), passando l’oggetto che risulta dal fitting come argomento. Ad esempio, riconsideriamo i dati dell’esperimento varietale a randomizzazione completa con tre repliche e quattro genotipi di avena, denominati A, B, C e D (Esempio 4.3). Se adattiamo ai risultati un semplice modello ANOVA ad una via (\(Y_i = \mu + \alpha_j + \varepsilon_i\)), le stime dei parametri con i relativi errori standard possono essere ottenute come mostrato nel riquadro sottostante.

# Standard errors for parameter estimates
# Input the data and fit the model (as in Chapter 4)
library(statforbiology)
dataset <- getAgroData("Oat1L")
mod6.1 <- lm(Yield ~ Genotype, data = dataset)
# Derive estimates and standard errors
summary(mod6.1)
## 
## Call:
## lm(formula = Yield ~ Genotype, data = dataset)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.17333 -0.08917  0.01833  0.07417  0.16333 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.58000    0.07566  60.531 6.17e-12 ***
## GenotypeB   -1.02667    0.10700  -9.595 1.16e-05 ***
## GenotypeC   -0.49667    0.10700  -4.642  0.00166 ** 
## GenotypeD    0.01667    0.10700   0.156  0.88008    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1311 on 8 degrees of freedom
## Multiple R-squared:  0.9412, Adjusted R-squared:  0.9192 
## F-statistic: 42.71 on 3 and 8 DF,  p-value: 2.866e-05

6.5 Come otteniamo il moltiplicatore \(k\)?

Per selezionare il moltiplicatore \(k\), dobbiamo considerare il coverage dell’intervallo di confidenza, ovvero la frequenza con cui esso “cattura” il valore reale della statistica della popolazione. Generalmente, maggiore è il valore di \(k\), maggiore è l’ampiezza dell’intervallo e maggiore è il coverage. Le informazioni di letteratura suggeriscono un coverage del 95%, corrispondente a una probabilità di errore del 5%; di conseguenza, dovremmo chiederci: quale valore di \(k\) consenta di raggiungere tale confidenza?

Abbiamo già visto che, se la sampling distribution fosse veramente gaussiana, \(k\) sarebbe all’incirca uguale a 2. Per determinare il coverage con questo valore di \(k\) possiamo utilizzare il metodo Monte Carlo; in relazione all’esempio iniziale, riguardante il pozzo inquinato con una sostanza erbicida, possiamo eseguire, ripetutamente, queste operazioni:

campioniamo tre individui da una popolazione gaussiana, con media pari a 120 e deviazione standard pari a 12;
adattiamo a questi tre individui il modello della media per ottenere una stima della media dell’intero pozzo, insieme al suo errore standard;
costruiamo un CI, utilizzando come moltiplicatore \(k = 2\). Se tale CI contiene il valore reale di 120 mg/L, l’esito è positivo e quindi assegniamo al risultato il valore 1 e lo immagazziniamo nel vettore ‘result’. Altrimenti assegniamo il valore 0 (funzione ifelse());;
ripetiamo i passaggi da 1 a 3 almeno per 100.000 volte e contiamo il numero di successi.

# Code box 6.4

# Monte Carlo simulation - 2
# Coverage of a confidence interval 
# depending on the multiplier k
# Sampling 3 reps from a gaussian with mean=120 and sd=12
mean <- 120
sigma <- 12
nrep <- 3
# nrep <- 20
k <- 2
# k <- qt(0.975, nrep - 1)
set.seed(1234)
result <- rep(0, 100000)
for (i in 1:100000){
  sample.i <- rnorm(nrep, mean, sigma)
  mod <- lm(sample.i ~ 1)
  m <- coef(mod)
  se <- summary(mod)$coef[1,2]
  limInf <- m - k * se
  limSup <- m + k * se
  # did we capture the mean?
  result[i] <- ifelse(limInf < 120 & limSup > 120, 1, 0)
}
sum(result)/100000
## [1] 0.81708

Il box sovrastante mostra che, impostando \(k = 2\) si ottiene un coverage molto basso (inferiore all’82%), corrispondente a una probabilità di errore di quasi il 19%, che è inaccettabile. Il problema è che la dimensione del campione è molto piccola e, pertanto, la distribuzione campionaria di \(m\) non è ben approssimata con una PDF gaussiana. Se la stessa simulazione viene eseguita con 20 repliche anziché 3, il coverage aumenta al 94% (provare per credere; basta cambiare la linea di codice nrep <- 3 con nrep <- 20). In pratica, utilizzare \(k = 2\) è ritenuto accettabile solo quando la dimensione del campione è superiore a 20-25 unità.

Per piccoli campioni (e in generale), è possibile ottenere un coverage esatto del 95% utilizzando il 97,5° percentile della distribuzione t di Student. Per ottenere questo valore, si può utilizzare la funzione qt() in R, che richiede, come minimo, due argomenti: il primo è il percentile desiderato, mentre il secondo rappresenta il numero di gradi di libertà per l’errore standard. Nel nostro esempio abbiamo tre repliche, quindi il numero di DF è 3 − 1 = 2 e il 97,5° percentile della distribuzione t di Student è pari a qt(0,975, 2) = 4,303, molto più alto di 2. In genere, il 97,5° percentile della distribuzione t di Student diminuisce all’aumentare del numero di gradi di libertà, tendendo ad 1,96, quando il numero di DF tende a \(\infty\). Se utilizziamo il codice sovrastante e sostituiamo alla linea k <- 2, il comando k <- qt(0.975, nrep - 1) possiamo confermare che il coverage diviene quasi esattamente del 95% (quasi, poiché il numero di simulazioni è molto alto, ma non infinito).

Se necessario, possiamo anche costruire un intervallo di confidenza del 99%, che riduce il rischio di errore all’1%. Basta utilizzare il 99,5° percentile di una distribuzione t di Student. In generale, se \(\alpha\) è il livello di confidenza desiderato, il percentile corrispondente è \(q_{\alpha} = 1 − (1 − \alpha/2)\) (quindi \(q_{0,05} = 1−(1−0,95)/2=0,975\) e \(q_{0,99} =1−(1−0,99)/2=0,995)\).

6.6 Gli intervalli di confidenza in pratica

6.6.1 Esempio 6.1: IC per una media campionaria

Immaginiamo di aver condotto un esperimento misurativo per determinare la resa media dei girasoli in un macro-ambiente dell’Italia centrale. Abbiamo quindi selezionato venti campi casuali in questo macro-ambiente ed abbiamo determinato i valori di resa riportati nel riquadro sottostante; sulla base di questi risultati, qual è la resa media nell’intero macro-ambiente? In questo esempio, la media campionaria è \(m = 58,68\) ed è una stima puntuale affidabile della resa media nell’intero macro-ambiente. Per calcolare il CI, dobbiamo determinare: 1. l’errore standard, che può essere facilmente calcolato utilizzando la semplice equazione riportata più sopra (\(\textrm{SEM} = {\sigma}/{\sqrt n}\)). La deviazione standard della popolazione \(\sigma\) è ignota, ma possiamo sostituirla con la deviazione standard del campione, che è 3,47 (principio del ‘plug-in’); 2. Il moltiplicatore \(k\), pari al 97,5° percentile della distribuzione t di Student (ovvero, 2,09). Di conseguenza, i due limiti dell’intervallo di confidenza sono rispettivamente 58,68 − 2,09 × 0,775 = 57,1 e 58,68 + 2,09 × 0,775 = 60,3. La conclusione è che, con un livello di confidenza del 95%, la resa media nel macro-ambiente rientra nell’intervallo tra 57,1 e 60,3.

# Example 6.1
# Confidence interval for a sample mean
# Input the sample and calculate the mean
Y <- c(54.08, 66.31, 56.17, 56.32, 52.01, 58.91, 58.74, 57.49,
59.57, 61.71, 56.89, 54.82, 56.88, 60.05, 59.39, 57.19,
64.76, 61.36, 62.03, 58.83)
m <- mean(Y)
m
## [1] 58.6755
## [1] 58.6755
# Calculate the standard error
s <- sd(Y)
SEM <- s/sqrt(length(Y))
SEM
## [1] 0.7754783
## [1] 0.7754783
# Determine the multiplier
k <- qt(0.975, length(Y) - 1)
k
## [1] 2.093024
## [1] 2.093024
# Calculate the limits of the CI # Lower limit
mean(Y) - k * SEM
## [1] 57.05241
## [1] 57.05241
# Higher limit mean(Y) + k * SEM ## [1] 60.29859

Più facilmente, possiamo pervenire allo stesso risultato stimando un modello della media, ed utilizzando la funzione confint(), come indicato nel riquadro sottostante.

# Example 6.1 [continuation]
# Retrieving confidence intervals from model fit
mod <- lm(Y ~ 1)
confint(mod)
##                2.5 %   97.5 %
## (Intercept) 57.05241 60.29859

6.6.2 Example 6.2: CIs for model parameters

Lo stesso approccio del riquadro sovrastante può essere utilizzato praticamente con ogni altro modello in R. Ad esempio, riconsiderando i dati ‘Oat1L’ dell’ Esempio 4.3 e stimando un modello ANOVA ad una via come nel riquadro 4.3, gli intervalli di confidenza per le stime dei parametri possono essere ottenuti come nel riquadro 6.7.

# Code box 6.7
# Example 6.2
# CIs for model parameters for the ’Oat1l’ data
# Load libraries and data library(statforbiology)
dataset <- getAgroData("Oat1L")
# Fit the model
mod6.1 <- lm(Yield ~ Genotype, data = dataset)
# CIs for model parameters 
confint(mod6.1)
##                  2.5 %     97.5 %
## (Intercept)  4.4055191  4.7544809
## GenotypeB   -1.2734199 -0.7799134
## GenotypeC   -0.7434199 -0.2499134
## GenotypeD   -0.2300866  0.2634199

6.7 Altri approcci per il calcolo dei CI

L’approccio proposto in questo capitolo si basa su due pre-requisiti fondamentali:

la distribuzione campionaria sia gaussiana (almeno approssimativamente), e
sia possibile, in qualche modo, calcolare un errore standard affidabile.

Nei casi in cui questi due pre-requisiti non siano soddisfatti, gli intervalli di confidenza possono essere determinati con altri approcci, come il metodo Monte Carlo (simile a quello utilizzato nel riquadro 6.2) o il metodo bootstrap (Chernick, 2011). Inoltre, vale la pena menzionare l’“Intervallo Credibile” (Credible Interval), che è la controparte bayesiana dell’intervallo di confidenza frequentista (Kruschke, 2011).

Questi metodi fanno parte della cosiddetta computer intensive statistic e possono essere molto utili in alcune circostanze, ma non saranno illustrati in dettaglio perché sono molto avanzati ed esulano dallo scopo di questo libro introduttivo.

6.8 Limitazioni del CI frequentista

L’intervallo di confidenza frequentista è ampiamente utilizzato nella letteratura scientifica, mentre la stima puntuale è spesso considerata inaccettabile. Ad esempio, le linee guida per gli autori di Weed Research, una rivista internazionale di alto livello nel campo delle scienze vegetali, affermano: “Tutti i valori stimati (ad esempio, parametri del modello, medie, differenze, ecc.) devono essere presentati insieme a un’adeguata misura di variabilità sia nel testo, che nelle tabelle e nei grafici”. Gli intervalli di confidenza, molto spesso, sono presentati nella forma più semplice “stima ± SE”, sebbene la copertura di tale intervallo sia piuttosto bassa. Basta comunque che il lettore sia avvisato sulla modalità utilizzata per la costruzione dell’intervallo presentato.

Per evitare gravi abusi interpretativi o di linguaggio, è necessario essere ben consapevoli dei limiti dell’intervallo di confidenza frequentista (Hastie et al., 2009), che deve essere sempre interpretato con riferimento ad una distribuzione campionaria, ovvero alle ipotetiche ripetizioni dello stesso esperimento con campioni diversi. Al contrario, è sbagliato interpretare il CI con riferimento ad ogni singolo esperimento; in altre parole, se il nostro intervallo di confidenza, determinato per uno specifico esperimento, va da 10 a 13, non è corretto affermare che il parametro incognito della popolazione è compreso tra 10 e 13 con una probabilità del 95% perché ciò non è vero (ricordate che l’IC cambia a ogni tentativo di campionamento; vedere il riquadro 6.4 e vedere anche Morey et al., 2016). Possiamo invece affermare che, nel lungo periodo, ripetendo lo stesso esperimento e continuando a calcolare gli intervalli di confidenza nello stesso modo, la nostra probabilità di errore si mantiene entro il 5%. Si tratta di una differenza piuttosto sottile, ma di fondamentale importanza!

6.9 Altre letture

Chernick MR (2011) An Introduction to Bootstrap Methods with Applications to R. Wiley, USA
Cochran WG, Cox GM (1950) Experimental design. John Wiley & Sons, Inc., USA
Hastie, T., Tibshirani, R., Friedman, J., 2009. The elements of statistical learning, Springer Series in Statistics. Springer Science + Business Media, California, USA.
Kruschke JK (2011) Doing bayesian data analyses. A tutorial with R and BUGS. Academic Press, Burlington, MA (USA)
Morey, RD, R Hoekstra, JN Rouder, MD Lee, E-J Wagenmakers, 2016. The fallacy of placing confidence in confidence intervals. Psychonomic Bulletin & Review 23, 103–123

6.10 Domande ed esercizi

In un campo di frumento sono state campionate trenta aree di saggio di un metro quadrato ciascuna, sulle quali è stata determinata la produzione. La media delle trenta aree è stata di 6.2 t/ha, con una varianza pari a 0.9. Stimare la produzione dell’intero appezzamento.
Siamo interessati a conoscere il contenuto medio di nitrati dei pozzi della media valle del Tevere. Per questo organizziamo un esperimento, durante il quale campioniamo 20 pozzi rappresentativi, riscontrando le concentrazioni riportate di seguito. Stimare la concentrazione media per l’intera valle del Tevere

38.3 38.6 38.1 39.9 36.3 41.6 37.0 39.8 39.1     
35.0 38.1 37.4 38.3 34.8 40.4 39.3 37.0 38.7    
38.2 38.4

E’stata impostata una prova sperimentale per confrontare due varietà di mais, con uno schema sperimentale a blocchi randomizzati con tre repliche. La prima varietà ha mostrato produzioni di 14, 12, 15 e 13 t/ha, mentre la seconda varietà ha mostrato produzioni pari a 12, 11, 10.5 e 13 t/ha. Stimare le produzioni medie delle due varietà, nell’ambiente di studio.
Un campione di 400 insetti a cui è stato somministrato un certo insetticida mostra che 136 di essi sono sopravvissuti. Determinare un intervallo di confidenza con grado di fiducia del 95% per la proporzione della popolazione insensibile al trattamento.
È stata studiata la risposta produttiva del sorgo alla concimazione azotata, con un esperimento i cui risultati sono riportati di seguito .Assumendo che la relazione sia lineare (retta), stimare la pendenza e l’intercetta della popolazione di riferimento, dalla quale è stato estratto il campione in studio. Utilizzare la funzione lm(Yield ~ Dose) ed estrarre gli errori standard con il metodo summary().

Dose	Yield
0	1.26
30	2.50
60	3.25
90	4.31
120	5.50

Utilizzando una simulazione Monte Carlo opportunamente pianificata, mostrare che la varianza del campione (uguale alla devianza divisa per il numero di individui meno uno) fornisce una stima più accurata della varianza della popolazione, rispetto allo scarto quadratico medio (devianza divisa per il numero di soggetti) che è invece uno stimatore distorto. Suggerimento: ricordare che uno stimatore accurato ha una distribuzione campionaria (sampling distribution) il cui valore atteso coincide con il valore da stimare.

Il teorema centrale del limite vale per campioni di dimensione elevata, composti da almeno 20-25 unità↩︎