Capitolo 11 La regressione lineare semplice
Nei capitoli precedenti abbiamo parlato di modelli basati su una fattori sperimentali in forma di categorie, ad esempio diversi erbicidi o diverse varietà. Abbiamo visto che, con questi fattori sperimentali, si utilizzano i cosiddetti modelli ANOVA.
Nella sperimentazione agronomica e, in genere, biologica, la variabile indipendente (o le variabili indipendenti) può (possono) rappresentare una quantità, come, ad esempio, la dose di un farmaco, il tempo trascorso da un certo evento, la fittezza di semina e così via. In questa condizione, l’analisi dei dati richiede modelli diversi da qualli visti finora, di solito identificati con il nome di modelli di regressione. Questa classe di modelli è estremamente interessante e si presta a sviluppi potentissimi. In questo libro ci accontenteremo di trattare la regressione lineare semplice, cioè un modello lineare (retta) con una variabile dipendente ed un regressore. In un capitolo successivo estenderemo le considerazioni fatte ai modelli non-lineari.
11.1 Caso studio: effetto della concimazione azotata al frumento
Per individuare la relazione tra la concimazione azotata e la produzione del frumento, è stato organizzato un esperimento a randomizzazione completa, con quattro dosi di azoto e quattro repliche. I risultati ottenuti sono riportati nella Tabella 11.1 e possono essere caricati direttamente da gitHub, con il codice sottostante. A differenza dei capitoli precedenti, in questo caso il dataset non è ottenuto da una prova vera, ma è stato generato, con il codice riportato nel capitolo 4. Pertanto, l’esempio, pur essendo efficace da un punto di vista didattico, potrebbe non essere totalmente realistico.
fileName <- "https://www.casaonofri.it/_datasets/NWheat.csv"
dataset <- read.csv(fileName, header=T)| Dose | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 21.98 | 25.69 | 27.71 | 19.14 |
| 60 | 35.07 | 35.27 | 32.56 | 32.63 |
| 120 | 41.59 | 40.77 | 41.81 | 40.50 |
| 180 | 50.06 | 52.16 | 54.40 | 51.72 |
11.2 Analisi preliminari
Questo esperimento è replicato ed è totalmente analogo a quello presentato nel capitolo 7, con l’unica differenza che, in questo caso, la variabile indipendente è quantitativa. Tuttavia, è del tutto logico considerare la dose di azoto come un predittore qualitativo (‘factor’) ed utilizzare un modello descrittivo ANOVA ad una via. Eseguiamo il ‘fitting’ con R, che è preceduto dalla trasformazione della variabile ‘dose’ in un fattore (funzione factor()).
dataset$DoseF <- factor(dataset$Dose)
model <- lm(Yield ~ DoseF, data = dataset)
anova(model)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## DoseF 3 1725.96 575.32 112.77 4.668e-09 ***
## Residuals 12 61.22 5.10
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Osserviamo che l’effetto del trattamento è significativo e il SEM è pari a \(\sqrt{5.10/4} = 1.129\). Prima di proseguire, verifichiamo che non ci siano problemi relativi alle assunzioni parametriche di base e che, quindi, la trasformazione dei dati non sia necessaria. I grafici dei residui, riportati in Figura 11.1, non mostrano patologie rilevanti.
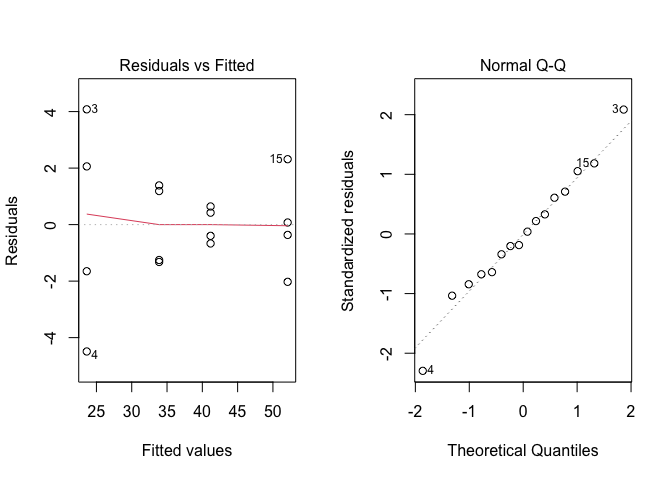
Figura 11.1: Analisi grafica dei residui per una prova di concimazione azotata del frumento
Da questo momento in avanti, diversamente a quanto abbiamo visto nei capitoli precedenti, l’analisi non prosegue con un test di confronto multiplo, che in questa situazione, se non del tutto errato, sarebbe comunque da considerare ‘improprio’. Infatti, quale senso avrebbe confrontare la risposta produttiva a 60 kg N ha-1 con quella a 120 kg N ha -1? In realtà noi non siamo specificatamente interessati a queste due dosi, ma a qualunque altra dose nell’intervallo da 0 a 180 kg N ha-1. Abbiamo selezionato quattro dosi per organizzare l’esperimento, ma resta il fatto che siamo interessati a definire una funzione di risposta per tutto l’intervallo delle dosi, non a confrontare le risposte a due dosi in particolare.
Per questo motivo, quando la variabile indipendente è una dose, l’analisi dei dati dovrebbe essere basata sull’impiego di un modello di regressione, in quanto ciò è più coerente con le finalità dell’esperimento, rispetto all’adozione di una procedura di confronto multiplo.
11.3 Definizione del modello lineare
Immaginiamo che, almeno nell’intervallo di dosi incluso nell’esperimento, l’effetto della concimazione azotata sulla produzione sia lineare. In effetti, l’andamento dei dati conferma questa impressione e, pertanto, poniamo il modello lineare nei termini usuali:
\[Y_i = b_0 + b_1 X_i + \varepsilon_i\]
dove \(Y\) è la produzione della parcella \(i\), trattata con la dose \(X_i\), \(b_0\) è l’intercetta (produzione a dose di azoto pari a 0) e \(b_1\) è la pendenza, cioè l’incremento di produzione per ogni incremento unitario della dose. La componente stocastica \(\varepsilon\) viene assunta omoscedastica e normalmente distribuita, con media 0 e deviazione standard \(\sigma\).
11.4 Stima dei parametri
Dobbiamo a questo punto individuare i parametri \(b_0\) e \(b_1\) in modo tale che la retta ottenuta sia la più vicina ai dati, cioè in modo da minimizzare gli scostamenti tra i valori di produzione osservati e quelli stimati dal modello (soluzione dei minimi quadrati). La funzione dei minimi quadrati è:
\[\begin{array}{l} Q = \sum\limits_{i = }^N {\left( {{Y_i} - \hat Y} \right)^2 = \sum\limits_{i = }^N {{{\left( {{Y_i} - {b_0} - {b_1}{X_i}} \right)}^2}} = } \\ = \sum\limits_{i = }^N {\left( {Y_i^2 + b_0^2 + b_1^2X_i^2 - 2{Y_i}{b_0} - 2{Y_i}{b_1}{X_i} + 2{b_0}{b_1}{X_i}} \right)} = \\ = \sum\limits_{i = }^N {Y_i^2 + Nb_0^2 + b_1^2\sum\limits_{i = }^N {X_i^2 - 2{b_0}\sum\limits_{i = }^N {Y_i^2 - 2{b_1}\sum\limits_{i = }^N {{X_i}{Y_i} + } } } } 2{b_0}{b_1}\sum\limits_{i = }^N {{X_i}} \end{array}\]
Calcolando le derivate parziali rispetto a \(b_0\) e \(b_1\) che, al momento, sono le nostre incognite, ed eguagliandole a 0 si ottengono le seguenti formule risolutive:
\[{b_1} = \frac{{\sum\limits_{i = 1}^N {\left[ {\left( {{X_i} - {\mu _X}} \right)\left( {{Y_i} - {\mu _Y}} \right)} \right]} }}{{\sum\limits_{i = 1}^N {{{\left( {{X_i} - {\mu _X}} \right)}^2}} }}\]
e:
\[{b_0} = {\mu _Y} - {b_1}{\mu _X}\]
Invece che svolgere i calcoli a mano, possiamo eseguire il fitting ai minimi quadrati con R; l’unica differenza tra questo modello di regressione e il modello ANOVA utilizzato poco sopra è che qui utilizziamo la variabile ‘Dose’ come tale, senza prima trasformarla in un ‘factor’.
modelReg <- lm(Yield ~ Dose, data = dataset)
summary(modelReg)
##
## Call:
## lm(formula = Yield ~ Dose, data = dataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6537 -1.5350 -0.4637 1.9250 3.9163
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 23.793750 0.937906 25.37 4.19e-13 ***
## Dose 0.154417 0.008356 18.48 3.13e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.242 on 14 degrees of freedom
## Multiple R-squared: 0.9606, Adjusted R-squared: 0.9578
## F-statistic: 341.5 on 1 and 14 DF, p-value: 3.129e-11Ora sappiamo che la relazione tra la dose di azoto e la risposta produttiva del frumento è:
\[ Y_i = 23.111 + 0.1544 \times X_i \]
L’elemento stocastico \(\varepsilon_i\) è normalmente distribuito, con media 0 e deviazione standard 2.029 (vedi la voce ‘Residual standard error’ nell’output sovrastante).
Come al solito, prima di qualunque altra considerazione, dobbiamo verificare la bontà del modello e il rispetto delle assunzioni di base, con una procedura che, per un modello di regressione, deve riguardare un maggior numero di aspetti rispetto ad un modello ANOVA.
11.5 Valutazione della bontà del modello
In primo luogo, è necessario verificare il rispetto delle assunzioni di base di normalità e omoscedasticità dei residui. Per questo, possiamo utilizzare gli stessi metodi impiegati per i modelli ANOVA, vale a dire un grafico dei residui verso gli attesi ed un QQ-plot dei residui standardizzati. In realtà, abbiamo già eseguito questo controllo con il modello ANOVA corrispondente e non vi è la necessità di ripeterlo con questo modello.
Dobbiamo invece assicurarci che i dati osservati siano ben descritti dal modello adottato, senza nessuna componente sistematica di mancanza d’adattamento. In altre parole, le osservazioni non debbono contraddire l’ipotesi che la risposta è lineare, salvo per le eventuali deviazioni casuali insite in qualunque esperimento. Per la verifica della bontà di adattamento possiamo utilizzare diverse procedure, che illustreremo di seguito.
11.5.1 Valutazione grafica
Nel modo più semplice, la bontà di adattamento può essere valutata attraverso un grafico dei valori attesi e dei valori osservati, come quello in Figura 11.2. Notiamo che non c’è alcun elemento che faccia pensare ad una sistematica deviazione rispetto alle previsioni fatte dal modello.
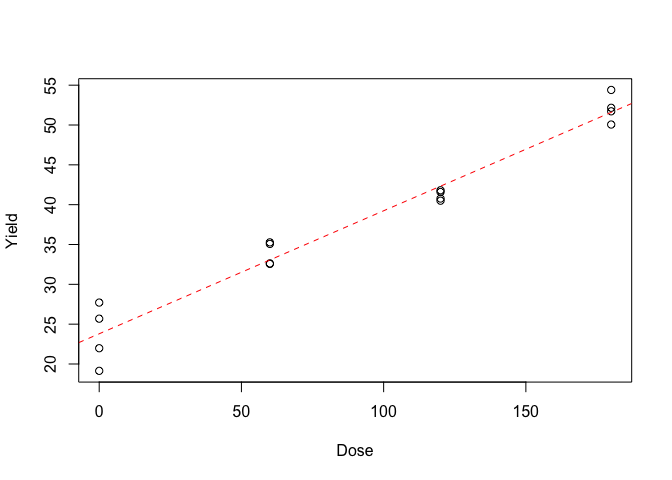
Figura 11.2: Risposta produttiva del frumento alla concimazione azotata: dati osservati (simboli) e valori attesi (linea tratteggiata).
11.5.2 Errori standard dei parametri
In secondo luogo, possiamo valutare gli errori standard delle stime dei parametri, che non debbono mai essere superiori alla metà del valore del parametro stimato, cosa che in questo caso è pienamente verificata. Se così non fosse, l’intervallo di confidenza del parametro, usualmente stimato utilizzando il doppio dell’errore standard, conterrebbe lo zero, il che equivarrebbe a dire che, ad esempio, la pendenza ‘vera’ (cioè quella della popolazione da cui il nostro campione è estratto) potrebbe essere nulla. In altre parole, la retta potrebbe essere ‘piatta’, dimostrando l’inesistenza di relazione tra la dose di concimazione e la produzione della coltura. Si può notare che, nell’esempio in studio, questo dubbio non sembra sussistere.
11.5.3 Test F per la mancanza d’adattamento
In terzo luogo, possiamo analizzare i residui della regressione, cioè gli scostamenti dei punti rispetto alla retta e, in particolare, la somma dei loro quadrati. Possiamo vedere che questo valore è pari a 70.37, ed è più alto di quello del corrispondente modello ANOVA, impiegato in precedenza (61.22):
anova(modelReg)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Dose 1 1716.80 1716.80 341.54 3.129e-11 ***
## Residuals 14 70.37 5.03
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Il risultato è perfettamente normale, dato che il residuo del modello ANOVA contiene solo la misura dello scostamento di ogni dato rispetto alla media del suo gruppo, che si può considerare ‘errore puro’, mentre il residuo della regressione, oltre all’errore puro, contiene anche una componente detta ‘mancanza d’adattamento’ (lack of fit), misurabile con lo scostamento di ogni media dalla linea di regressione. In effetti, la regressione lineare è solo un’approssimazione della reale relazione biologica tra la concimazione e la produzione del frumento.
Insomma, il modello di regressione è un modello che ha sempre minor capacità descrittiva rispetto ad un modello ANOVA. La differenza può essere quantificata utilizzando le devianze dei rispettivi residui:
\[\textrm{Lack of fit} = 70.37 - 61.22 = 9.15\]
Bisogna però anche dire che il modello di regressione è più parsimonioso, nel senso che ci ha costretto a stimare solo due parametri (\(b_0\) e \(b_1\)), mentre il modello ANOVA ce ne ha fatti stimare quattro (\(\mu\), \(\alpha_2\), \(\alpha_3\) e \(\alpha_4\), considerando che \(\alpha_1 = 0\)). Quindi il residuo del modello di regressione ha 14 gradi di libertà (16 dati meno due parametri stimati), mentre il residuo del modello ANOVA ne ha 12 (16 - 4). La componente di lack of fit ha quindi 14 - 12 = 2 gradi di libertà. Ci chiediamo, questa componente di lack of fit è significativamente più grande dell’errore puro?
L’ipotesi nulla di assenza di lack of fit può essere testata con un test di F, per il confronto di due varianze: se questo è significativo allora la componente di mancanza d’adattamento non è trascurabile, ed il modello di regressione dovrebbe essere rifiutato. L’espressione è:
\[ F_{lack} = \frac{\frac{RSS_r - RSS_a}{DF_r-DF_a} } {\frac{RSS_a}{DF_a}} = \frac{MS_{lack}}{MSE_a}\]
dove RSSr è la devianza residua della regressione con i sui gradi di liberta DFr e RSSa è la devianza residua del modello ANOVA, con i suoi gradi di libertà DFa. In R, il test F per la mancanza d’adattamento può essere eseguito con la funzione anova(), confrontando i due modelli alternativi:
anova(modelReg, model)
## Analysis of Variance Table
##
## Model 1: Yield ~ Dose
## Model 2: Yield ~ DoseF
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 14 70.373
## 2 12 61.219 2 9.1542 0.8972 0.4334Vediamo che non otteniamo risultati significativi (P = 0.4334). Ciò supporta l’idea che non vi sia mancanza d’adattamento e quindi la regressione fornisca una descrizione altrettanto adeguata dei dati sperimentali rispetto al più ‘complesso’ modello ANOVA. Scegliamo quindi il modello di regressione, in quanto più semplice, nel rispetto del principio del rasoio di Occam.
11.5.4 Test F per la bontà di adattamento
Abbiamo dimostrato che il modello di regressione non è significativamente peggiore del modello ANOVA corrispondente. Un approccio alternativo per dimostrare la bontà di adattamento è verificare se il modello di regressione è significativamente migliore di un modello ‘nullo’. Ricordiamo che con il modello ‘nullo’ (\(Y_i = \mu + \varepsilon_i\)) si assume che la risposta sia costante e pari alla media di tutti i dati, escludendo così ogni effetto della dose di concimazione. La devianza del residuo di un modello nullo non è altro che la devianza totale dei dati, che risulta pari a 1787.178:
modNull <- lm(Yield ~ 1, data = dataset)
deviance(modNull)
## [1] 1787.178Abbiamo visto che la devianza del modello di regressione è pari a 70.37: la differenza (1716.81) rappresenta la ‘bontà di adattamento’, cioè una misura di quanto migliora il potere descrittivo del modello aggiungendo l’effetto ‘dose’. Quindi, un test di F per la bontà di adattamento può essere costruito come:
\[ F_{good} = \frac{\frac{RSS_t - RSS_r}{DF_t - DF_r} } {\frac{RSS_r}{DF_r}} = \frac{MS_{good}}{MSE_r}\]
dove RSSt è la devianza totale dei dati con i sui gradi di liberta DFt. In R, il test F per la bontà d’adattamento può essere eseguito con la funzione anova(), senza la necessità di includere come argomento il modello ‘nullo’:
anova(modelReg)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Dose 1 1716.80 1716.80 341.54 3.129e-11 ***
## Residuals 14 70.37 5.03
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vediamo che in questo caso l’ipotesi nulla deve essere rifiutata: la varianza spiegata dalla regressione è significativamente maggiore di quella del residuo.
11.5.5 Coefficiente di determinazione
Nella letteratura scientifica si è sempre sentita l’esigenza di una statistica che rappresentasse, in modo sintetico, la bontà della regressione. Per questo scopo si è sempre utilizzato il rapporto tra la devianza spiegata dalla regressione e la devianza totale, detto coefficiente di determinazione o R2:
\[R^2 = \frac{SS_{reg}}{SS_{tot}} = \frac{1716.81}{1787.18} = 0.961\]
Questa statistica varia da 0 ad 1; in quest’ambito, più è alto il valore tanto migliore è la bontà della regressione. Il coefficiente di determinazione è visibile nell’output della funzione summary() applicata all’oggetto ‘modelReg’ (vedi più sopra).
11.6 Previsioni
Dato che il modello ha mostrato di funzionare bene, con prudenza, possiamo utilizzarlo per effettuare due tipi di previsioni: diretta ed inversa. Nel primo caso, possiamo prevedere la risposta per una qualunque dose, nel secondo caso, possiamo prevedere la dose che ha indotto una data risposta (Figure 11.3).
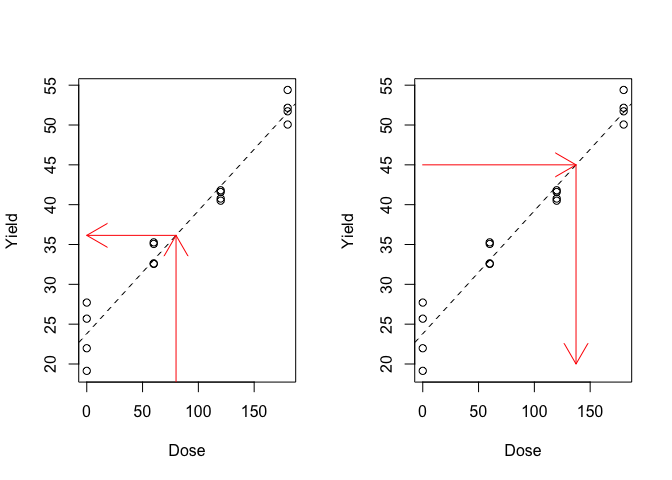
Figura 11.3: Esempio di previsioni: a destra, previsione della risposta per una data dose, a sinistra previsione della dose per ottenere una data risposta
Per entrambi i tipi di previsione ci si dovrebbe mantenere entro i livelli di dosi e risposte massimi e minimi inclusi ed osservati in prova, per evitare pericolose estrapolazioni (la risposta ha mostrato di essere lineare solo nell’intervallo osservato, ma non sappiamo cosa potrebbe capitare fuori da questo).
I parametri stimati possono essere facilmente utilizzati per fare previsioni dirette, come indicato nel box sottostante.
23.793750 + 0.154417 * 30
## [1] 28.42626
23.793750 + 0.154417 * 80
## [1] 36.14711Anche queste stime, come tutte le altre, si riferiscono al campione in prova, mentre noi siamo interessati a fornire una previsione per l’intera popolazione da cui i nostri dati sono capionati. Per questo motivo, abbiamo la necessità di quantificare l’incertezza, attraverso un’opportuna stima dell’errore standard. In R, ciò è possibile utilizzando la funzione predict(), passando come argomento le dosi alle quali effettuare la previsione, organizzate in un data frame. Ad esempio, se si vuole prevedere la produzione a 30 e 80 kg N ha-1, il codice è:
pred <- predict(modelReg, newdata=data.frame(Dose=c(30, 80)), se=T)
pred
## $fit
## 1 2
## 28.42625 36.14708
##
## $se.fit
## 1 2
## 0.7519981 0.5666999
##
## $df
## [1] 14
##
## $residual.scale
## [1] 2.242025E’anche possibile effettuare la previsione inversa, cioè chiedere ai dati qual è la dose a cui corrisponde una produzione di 45 q/ha. In questo caso dobbiamo tener presente che l’equazione inversa è:
\[X = \frac{Y - b_0}{b_1}\] e la previsione corrispondente è:
(45 - 23.793750)/0.154417
## [1] 137.3311Per determinare l’errore standard possiamo utilizzare la funzione deltaMethod(), nel package ‘car’, che ci calcola anche gli errori standard con il metodo della propagazione degli errori:
car::deltaMethod(modelReg, "(45 - b0)/b1",
parameterNames=c("b0", "b1"))
## Estimate SE 2.5 % 97.5 %
## (45 - b0)/b1 137.3314 4.4424 128.6244 146.04Il procedimento sopra descritto è molto comune, per esempio nei laboratori chimici, dove viene utilizzato nella fase di calibrazione di uno strumento. Una volta che la retta di calibrazione è stata individuate, essa viene utilizzata per determinare le concentrazioni incognite di campioni per i quali sia stata misurata la risposta.
11.7 Disegni a blocchi randomizzati
Come abbiamo gà detto, la gran parte degli esperimenti agronomici, inclusi quelli in cui si organizzano per studiare l’effetto di una variabile quantitativa, sono disegnati a blocchi randomizzati. In questo caso, oltre all’effetto in studio, esiste anche l’effetto del blocco, che non può essere trascurato, altrimenti si viene ad inficiare l’indipendenza dei residui, come abbiamo evidenziato nel capitolo precedente.
Per una banale esempio, potremmo immaginare che nel dataset ’NWheat, le quattro repliche di ogni dose siano state ottenute, nell’ordine, nei blocchi 1, 2, 3 e 4. Il modello lineare risulterebbe così modificato:
\[Y_{ij} = b_0 + \gamma_j + b_1 X_{ij} + \varepsilon_{ij}\] vale a dire: la produzione per la i-esima dose di azoto nel j-esimo blocco è ottenuta attraverso un modello lineare, in cui l’effetto del blocco si ripercuote sull’intercetta, che, nei diversi blocchi è pari, rispettivamente, a \(b_0 + \gamma_1\), \(b_0 + \gamma_2\), \(b_0 + \gamma_3\) e \(b_0 + \gamma_4\). In questo modo l’effetto del blocco è fisso ed additivo; ovviamente si possono anche adottare approcci più complessi, che però esulano dagli scopi del nostro testo introduttivo.
Il fitting di questo modello è semplice, utilizzando il codice seguente:
# creazione della variabile blocco
dataset$Block <- factor(rep(1:4, 4))
model <- lm(Yield ~ Dose + Block, data = dataset)Ovviamente, il riferimento per testare la mancanza di adattamento sarà il modello ANOVA corrispondente, a blocchi randomizzati; per il resto, non cambia nulla. Resta però la necessità di conoscere i parametri della curva dose-risposta media per i diversi blocchi, che sarà quella da utilizzare per fare previsioni. Utilizziamo quindi il metodo ‘summary()’ come abbiamo visto in precedenza.
summary(model)
##
## Call:
## lm(formula = Yield ~ Dose + Block, data = dataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.960 -1.455 -0.170 1.394 2.527
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 23.277500 1.247516 18.659 1.12e-09 ***
## Dose 0.154417 0.007722 19.997 5.35e-10 ***
## Block2 1.297500 1.465133 0.886 0.395
## Block3 1.945000 1.465133 1.328 0.211
## Block4 -1.177500 1.465133 -0.804 0.439
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.072 on 11 degrees of freedom
## Multiple R-squared: 0.9736, Adjusted R-squared: 0.964
## F-statistic: 101.3 on 4 and 11 DF, p-value: 1.331e-08Vediamo che la pendenza è pari a 0.1544 ed è esattamente identica a quella stimata senza considerare l’effetto del blocco. L’intercetta, invece, cambia al cambiare del blocco. In particolare, R impiega una parametrizzazionecon vincolo sul trattamento e quindi il valore 23.2775, che vediamo identificato come intercetta, corrisponde al primo blocco (in quanto il vincolo è \(\gamma_1 = 0\)).
Dobbiamo quindi calcolare un’intercetta media dei blocchi, ad esempio utilizzando la solita funzione ‘emmeans()’, che fornisce la risposta produttiva attesa (media) per un livello di concimazione pari a 0. Il codice è il seguente:
library(emmeans)
emmeans(model, ~1, at = list(Dose = 0))
## 1 emmean SE df lower.CL upper.CL
## overall 23.8 0.867 11 21.9 25.7
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95Il valore è identico a quello ottenuto senza considerare l’effetto del blocco, anche se l’errore standard è diverso in quanto parte del residuo è stata spiegata appunto attraverso l’effetto del blocco.
Prima di concludere, vorremmo menzionare un’approccio alternativo, che consiste nell’utilizzare una parametrizzazione con vincolo sulla somma, invece che sul trattamento. Con questo vincolo, analogamente a quanto abbiamo visto nel capitolo 7, l’intercetta stimata con la regressione rappresenta il valor medio e gli effetti dei blocchi sono stimati come scostamenti rispetto al valor medio. Per imporre un vincolo sulla somma basta modificare il codice di fitting nel modo indicato di seguito. Nell’output non è presente l’effetto del quarto blocco, in quanto, per il vincolo prescelto, deve essere tale che sommato agli altri tre restituisca 0.
model <- lm(Yield ~ Dose + Block, data = dataset,
contrasts = list(Block = "contr.sum"))
summary(model)
##
## Call:
## lm(formula = Yield ~ Dose + Block, data = dataset, contrasts = list(Block = "contr.sum"))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.960 -1.455 -0.170 1.394 2.527
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 23.793750 0.866785 27.451 1.75e-11 ***
## Dose 0.154417 0.007722 19.997 5.35e-10 ***
## Block1 -0.516250 0.897207 -0.575 0.577
## Block2 0.781250 0.897207 0.871 0.402
## Block3 1.428750 0.897207 1.592 0.140
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.072 on 11 degrees of freedom
## Multiple R-squared: 0.9736, Adjusted R-squared: 0.964
## F-statistic: 101.3 on 4 and 11 DF, p-value: 1.331e-0811.8 Altre letture
- Draper, N.R., Smith, H., 1981. Applied Regression Analysis, in: Applied Regression. John Wiley & Sons, Inc., IDA, pp. 224–241.
- Faraway, J.J., 2002. Practical regression and Anova using R. http://cran.r-project.org/doc/contrib/Faraway-PRA.pdf, R.