Capitolo 10 Modelli ANOVA con fattori di blocco
Nel capitolo 7 abbiamo impiegato un modello ANOVA con una sola variabile indipendente categorica, assumendo che le unità sperimentali, escluso l’effetto del trattamento, fossero totalmente indipendenti tra di loro. Questa assunzione era totalmente realistica, poiché si trattava di un disegno sperimentale a randomizzazione completa, dove non sussistevano raggruppamenti di alcun tipo, escluso quello dettato dal trattamento in studio.
Se invece l’esperimento include uno o più blocking factors, le osservazioni che appartengono allo stesso blocco sono più simila tra loro delle osservazioni che appartengono a blocchi diversi, proprio perché condividono le condizioni del blocco stesso. Per non invalidare l’indipendenza dei residui dobbiamo definire un modello ANOVA che tenga conto anche dei fattori di raggruppamento, in modo che il loro effetto non sia trascurato e, di conseguenza, si sommi agli effetti residui. Come al solito, affrontiamo questo tema partendo da alcuni esempi pratici.
10.1 Caso-studio: confronto tra erbicidi in campo
Abbiamo una prova di confronto tra erbicidi in mais, con 13 formulati, due testimoni inerbiti (che, per comodità, considereremo due trattamenti diversi) e un testimone scerbato. Al momento di impiantare la prova, era lecito ipotizzare che, pur scegliendo un appezzamento il più omogeneo possibile, avremmo potuto riscontrare differenze di infestazione tra un punto e l’altro del campo, con un presumibile gradiente procedendo dai lati (vicino alle fosse) verso il centro. In questa situazione, se l’esperimento fosse stato disegnato a randomizzazione completa, le differenze di infestazione tra una parte e l’altra del campo sarebbero state trascurate e avrebbero finito per incrementare l’errore sperimentale, diminuendo l’efficienza dell’esperimento.
Abbiamo quindi impiegato un disegno a blocchi randomizzati con quattro repliche; il campo è stato suddiviso in tante sezioni (dette blocchi) quante erano le repliche (quattro), perpendicolarmente al gradiente di infestazione trasversale. In questo modo, l’ambiente era relativamente omogeneo all’interno di ciascun blocco, nel quale è stata collocata una replica per trattamento.
Il dataset dei risultati (‘rimsulfuron.csv’) è disponibile nella solita repository online. Nel box sottostante, carichiamo il file e trasformiamo le due variabili esplicative (blocco e trattamento) in fattori sperimentali. Più sotto, mostriamo la tabella in formato ‘WIDE’ (una riga per trattamento, con le repliche sulle colonne), con le medie di riga (trattamento) e di colonna (blocco)
fileName <- "https://www.casaonofri.it/_datasets/rimsulfuron.csv"
rimsulfuron <- read.csv(fileName)
rimsulfuron$Code <- factor(rimsulfuron$Code)
rimsulfuron$Herbicide <- factor(rimsulfuron$Herbicide)
rimsulfuron$Block <- factor(rimsulfuron$Block)## 1 2 3 4 Medie
## Alachlor + terbuthylazine 12.060 49.580 41.340 16.370 29.838
## Hand-Weeded 77.580 92.080 86.590 99.630 88.970
## Metolachlor + terbuthylazine (pre) 51.770 52.100 49.460 34.670 47.000
## Pendimethalin (post) + rimsuulfuron (post) 94.820 87.720 102.050 101.940 96.632
## Pendimethalin (pre) + rimsulfuron (post) 65.510 88.720 95.520 82.390 83.035
## Rimsulfuron (40) 85.910 91.090 111.420 93.150 95.392
## Rimsulfuron (45) 93.030 105.000 89.190 79.040 91.565
## Rimsulfuron (50) 86.930 105.820 110.020 89.100 97.968
## Rimsulfuron (50+30 split) 71.360 77.570 115.910 92.160 89.250
## Rimsulfuron (60) 52.990 102.860 100.620 97.040 88.377
## Rimsulfuron + Atred 94.110 89.860 104.340 99.630 96.985
## Rimsulfuron + hoeing 73.220 86.060 118.010 98.320 93.903
## Rimsulfuron + thyfensulfuron 75.280 82.590 94.960 85.850 84.670
## Thifensulfuron 78.470 42.320 62.520 24.340 51.913
## Unweeded 1 10.880 31.770 23.920 20.850 21.855
## Unweeded 2 27.580 51.550 25.130 38.610 35.718
## Medie 65.719 77.293 83.188 72.068 74.56710.2 Definizione di un modello lineare
La produzione di ogni unità sperimentale (parcella) è condizionata da più di un effetto:
- il diserbante con cui essa è stata trattata;
- il blocco di cui essa fa parte;
- ogni altro effetto non conoscibile e puramente casuale (residuo).
Il modello è quindi:
\[ Y_{ij} = \mu + \gamma_i + \alpha_j + \varepsilon_{ij}\]
dove \(Y\) è la produzione nel blocco \(i\) e con il diserbo \(j\), \(\mu\) è l’intercetta, \(\gamma\) è l’effetto del blocco \(i\), \(\alpha\) è l’effetto del trattamento \(j\) e \(\varepsilon\) è l’errore sperimentale per ogni singola parcella, che si assume normalmente distribuito, con media 0 e deviazione standard \(\sigma\). Anche in questo caso, come nel capitolo 7, poniamo un vincolo sulla somma degli effetti del trattamento e del blocco (\(\sum \gamma_i = 0\) e \(\sum \alpha_j = 0\)), in modo che \(\mu\) rappresenti la media generale. In totale, vi sono 19 parametri da stimare (un’intercetta, 15 effetti dei trattamenti e tre effetti dei blocchi, più \(\sigma\)).
10.3 Stima dei parametri
10.3.1 Coefficienti del modello
In questo caso l’esperimento è completamente bilanciato e la stima dei parametri può essere fatta banalmente, considerando i valori osservati e le medie aritmetiche per gruppo. Per prima cosa, calcoliamo tutte le medie (generale, dei blocchi e dei trattamenti), come mostrato nel box sottostante.
mu <- mean(rimsulfuron$Yield)
mu_bl <- with(rimsulfuron, tapply(Yield, Block, mean))
mu_tr <- with(rimsulfuron, tapply(Yield, Code, mean))
mu
## [1] 74.56687
mu_bl
## 1 2 3 4
## 65.71875 77.29313 83.18750 72.06812
mu_tr
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
## 95.3925 91.5650 97.9675 88.3775 89.2500 84.6700 93.9025 83.0350 96.6325 96.9850 51.9125 47.0000 29.8375 88.9700 21.8550 35.7175L’effetto dei blocchi si calcola sottraendo dalle relative medie la media generale, mentre l’effetto dei trattamenti si calcola in modo analogo, sostituendo alla media dei blocchi la media dei trattamenti.
gamma <- mu_bl - mu
alpha <- mu_tr - muA questo punto, per ogni osservazione, possiamo calcolare il valore atteso, sommando i valori \(\mu\), \(\gamma\) ed \(\alpha\) corrispondenti; inoltre, possiamo calcolare i residui, come scostamenti tra i valori osservati e i valori attesi. La tabella sottostante schematizza i calcoli necessari per le prime otto osservazioni e mostra come la somma degli elementi del modello restituisca le osservazioni originali.
gamma <- gamma[rimsulfuron$Block]
alpha <- alpha[rimsulfuron$Code]
res <- data.frame(Yield = rimsulfuron$Yield,
mu = mu, gamma = gamma, alpha = alpha,
Atteso = mu + gamma + alpha)
res$Residuo = res$Yield - res$Atteso
res$Verifica = res$Atteso + res$Residuo
print(round(res, 2)[1:8,])
## Yield mu gamma alpha Atteso Residuo Verifica
## 1 85.91 74.57 -8.85 20.83 86.54 -0.63 85.91
## 2 93.03 74.57 -8.85 17.00 82.72 10.31 93.03
## 3 86.93 74.57 -8.85 23.40 89.12 -2.19 86.93
## 4 52.99 74.57 -8.85 13.81 79.53 -26.54 52.99
## 5 71.36 74.57 -8.85 14.68 80.40 -9.04 71.36
## 6 75.28 74.57 -8.85 10.10 75.82 -0.54 75.28
## 7 73.22 74.57 -8.85 19.34 85.05 -11.83 73.22
## 8 65.51 74.57 -8.85 8.47 74.19 -8.68 65.5110.3.2 Stima di \(\sigma\)
In primo luogo, calcoliamo la devianza dei residui, come somma dei loro quadrati; da questa, possiamo ottenere la deviazione standard (\(\sigma\)), considerando che abbiamo 16 gruppi con quattro repliche, quindi tre gradi di libertà per gruppo. Tuttavia, dobbiamo anche tener presente che le repliche di ogni gruppo non differiscono solo per motivi casuali, ma anche perché appartengono a blocchi diversi. Abbiamo quattro blocchi, quindi tre gradi di libertà, che vanno dedotti dai 48 (16 x 3) precedentemente calcolati.
RSS <- sum( res$Residuo^2 )
sigma <- sqrt(RSS/45)
RSS; sigma
## [1] 7187.348
## [1] 12.63799Da \(\sigma\) possiamo ottenere anche SEM e SED, anche se questo calcolo ve lo lascio per esercizio (ricordate che abbiamo quattro repliche per trattamento).
10.4 Scomposizione della varianza
La scomposizione della varianza è analoga a quella che abbiamo operato per l’ANOVA ad una via; tuttavia, dobbiamo tener presente che, in questo caso, la devianza totale delle osservazione deve essere decomposta in tre quote: una dovuta al trattamento, una dovuta al blocco ed una dovuta agli effetti stocastici.
La devianza dei residui l’abbiamo già calcolata, mentre la devianza dei trattamenti possiamo calcolarla come somma dei quadrati degli scarti del vettore ‘alpha’. Analogamente, possiamo ottenere la devianza dei blocchi, considerando il vettore ‘gamma’.
TSS <- sum(res$alpha^2)
BSS <- sum(res$gamma^2)
TSS; BSS
## [1] 43931.23
## [1] 2660.491Verifichiamo che la devianza del trattamento, sommata alle devianze dei blocchi e dei residui restituisce la devianza totale delle osservazioni (somma dei quadrati degli scarti rispetto alla media generale).
TSS + BSS + RSS
## [1] 53779.07
sum( (rimsulfuron$Yield - mu)^2 )
## [1] 53779.07Ci chiediamo se gli effetti attribuibili ai blocchi e ai trattamenti siano significativamente più grandi degli effetti stocastici. Sappiamo già di non poter confrontare le devianze, ma possiamo calcolare e confrontare con un test di F le relative varianze. Basta tener conto che i gradi di libertà dei blocchi e dei trattamenti sono rispettivamente 3 e 15, cioè il numero dei blocchi meno uno e il numero dei trattamenti meno uno.
MSt <- TSS/15
MSb <- BSS/3
MSe <- RSS/45La significatività della differenza tra blocchi è poco rilevate, mentre siamo interessati a valutare la significatività della differenza tra trattamenti con un apposito test di F:
Fratio <- MSt/MSe
Fratio
## [1] 18.3369Il valore osservato si mostra abbastanza discrepante rispetto all’ipotesi nulla, che possiamo porre nella forma \(H_0: \mu_1 = \mu_2 = ... = \mu_{16} = \mu\). Notate come stiamo facendo riferimento alle medie delle 16 popolazioni che hanno generato i nostri campioni, assumendole uguali tra di loro, come se i 16 campioni fossero stati, nella realtà, estratti dalla stessa popolazione. Ancora una volta, come nel capitolo 7, vedete che stiamo anche assumendo che le varianze delle 16 popolazioni siano omogenee.
Ci chiediamo, che possibilità esiste che, nonostante l’ipotesi nulla sia vera, noi osserviamo un valore di F così alto o più alto? Potremmo determinare la sampling distribution per F attraverso una simulazione di Monte Carlo, oppure, assumendo che i residui siano gaussiani, possiamo utilizzare la funzione di densità F di Fisher, con 15 gradi di libertà al numeratore e 45 gradi di libertà al denominatore.
pf(Fratio, 15, 45, lower.tail = F)
## [1] 2.328653e-14Vediamo che la probabilità che l’ipotesi nulla sia vera è molto piccola e, pertanto, rifiutiamo l’ipotesi nulla, accettando l’alternativa: esiste in effetti una differenza significativa tra i trattamenti erbicidi.
10.5 Adattamento del modello con R
Il model fitting può essere comodamente effettuato con R, utilizzando la funzione lm(), come mostrato nel box sottostante. Per brevità, utilizziamo il codice del trattamento erbicida invece che il nome.
mod <- lm(Yield ~ Block + Code, data = rimsulfuron)La tabella ANOVA può essere facilmente ottenuta con la funzione anova():
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Block 3 2660 886.83 5.5524 0.002496 **
## Code 15 43931 2928.75 18.3369 2.329e-14 ***
## Residuals 45 7187 159.72
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Ovviamente, prima di considerare questa tabella dovremo preoccuparci del fatto che le assunzioni di base siano rispettate (vedi capitolo 8), cosa che possiamo facilmente verificare con un’analisi grafica dei residui, utilizzando il codice sottostante. L’output è visibile in Figura 10.1.
par(mfrow=c(1,2))
plot(mod, which = 1)
plot(mod, which = 2)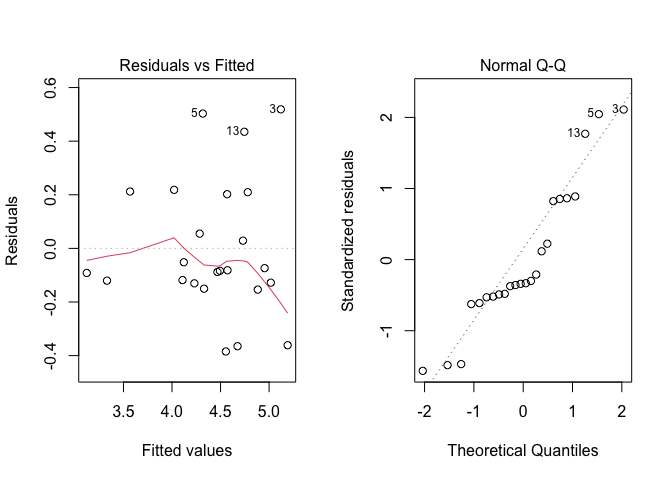
Figura 10.1: Analisi grafica dei residui per la prova di confronto erbicida
Dopo esserci rassicurati su questo importante aspetto, possiamo vedere che abbiamo due ipotesi nulle da testare (effetto dei trattamenti non significativo ed effetto dei blocchi non significativo), che possono essere entrambe rifiutate per P < 0.05.
Da questo punto in avanti, l’analisi procede come usuale, calcolando le medie marginali attese ed, eventualmente, confrontandole tra loro con una procedura di confronto multiplo, come descritto nei capitoli precedenti. Tener presente che, in questo esperimento, abbiamo 16 trattamenti, cioè \(16 \times 15 / 2 = 120\) confronti; di conseguenza, è opportuno operare la correzione per la molteplicità. Inoltre, dato che il trattamento più interessante è quello che rende massima la produzione, sarà opportuno ordinare le medie in senso decrescente, utilizzando l’argomento ‘reverse = T’.
library(emmeans)
medie <- emmeans(mod, ~Code)
multcomp::cld(medie, Letters = LETTERS, reverse = T)
## Code emmean SE df lower.CL upper.CL .group
## 3 98.0 6.32 45 85.24 110.7 A
## 10 97.0 6.32 45 84.26 109.7 A
## 9 96.6 6.32 45 83.91 109.4 A
## 1 95.4 6.32 45 82.67 108.1 A
## 7 93.9 6.32 45 81.18 106.6 A
## 2 91.6 6.32 45 78.84 104.3 A
## 5 89.2 6.32 45 76.52 102.0 A
## 14 89.0 6.32 45 76.24 101.7 A
## 4 88.4 6.32 45 75.65 101.1 A
## 6 84.7 6.32 45 71.94 97.4 A
## 8 83.0 6.32 45 70.31 95.8 AB
## 11 51.9 6.32 45 39.19 64.6 BC
## 12 47.0 6.32 45 34.27 59.7 C
## 16 35.7 6.32 45 22.99 48.4 C
## 13 29.8 6.32 45 17.11 42.6 C
## 15 21.9 6.32 45 9.13 34.6 C
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 16 estimates
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.Vi lascio il commento dei risultati come esercizio.
10.6 Disegni a quadrato latino
A volte i fattori di blocco sono più di uno e danno origine ad un disegno sperimentale detto ‘quadrato latino’ di cui abbiamo parlato nel capitolo 3. Qui, forniremo un esempio tratto dalla pratica sperimentale industriale.
10.7 Caso studio: confronto tra metodi costruttivi
Immaginiamo di voler studiare il tempo necessario per costruire un componente elettronico, utilizzando quattro metodi diversi: è evidente che il tempo di costruzione sarà influenzato dalla perizia del tecnico e, per questo, utilizziamo quattro tecnici diversi, ad ognuno dei quali facciamo utilizzare tutti e quattro i metodi. Un esperimento così disegnato sarebbe a blocchi randomizzati, con il tecnico che fa da blocco per i trattamenti. Tuttavia, dobbiamo anche riconoscere che i quattro tecnici saranno via via meno efficienti, e quindi il metodo che utilizzeranno per primo sarà avvantaggiato, mentre quello che utilizzeranno per ultimo sarà svantaggiato. E’vero che i metodi sono assegnati in ordine random ad ogni tecnico, ma non si può comunque evitare che un metodo venga avvantaggiato rispetto ad un altro, perché, ad esempio, non viene mai ad occupare l’ultima posizione (o meglio, l’ultimo turno). Abbiamo già illustrato questa situazione in un capitolo precedente ed abbiamo visto come essa possa essere gestita imponendo un vincolo ulteriore alla randomizzazione e facendo in modo che ogni metodo occupi tutte e quattro i turni, in tecnici diversi. Il disegno è quindi a quadrato latino.
Il dataset dei risultati è disponibile online:
fileName <- "https://www.casaonofri.it/_datasets/Technicians.csv"
dataset <- read.csv(fileName, header=T)
dataset
## Shift Technician Method Time
## 1 I Andrew C 90
## 2 II Andrew B 90
## 3 III Andrew A 89
## 4 IV Andrew D 104
## 5 I Anna D 96
## 6 II Anna C 91
## 7 III Anna B 97
## 8 IV Anna A 100
## 9 I Michael A 84
## 10 II Michael D 96
## 11 III Michael C 98
## 12 IV Michael B 104
## 13 I Sarah B 88
## 14 II Sarah A 88
## 15 III Sarah D 98
## 16 IV Sarah C 10610.8 Definizione di un modello lineare
In questo caso abbiamo un trattamento (metodo) e due effetti ‘blocco’ (tecnico e turno) da includere nel modello, che può essere così definito:
\[Y_{ijk} = \mu + \gamma_k + \beta_j + \alpha_i + \varepsilon_{ijk}\]
dove \(\mu\) è l’intercetta, \(\gamma\) è l’effetto del turno k, \(\beta\) è l’effetto del tecnico j e \(\alpha\) è l’effetto del metodo i. L’elemento \(\varepsilon_{ijk}\) rappresenta la componente random individuale, di ogni osservazione e si assume normalmente distribuita, con media 0 e deviazione standard \(\sigma\).
Avendo già illustrato il processo di stima dei parametri e di scomposizione della varianza, quindi utilizziamo subito R per il ‘model fitting’:
mod <- lm(Time ~ Method + Technician
+ Shift, data = dataset)Verifichiamo il rispetto delle assunzioni di base, con l’analisi grafica dei residui, riportata in Figura 10.2 (il codice è analogo a quello fornito più sopra).

Figura 10.2: Analisi grafica dei residui per la prova di confronto tra metodi costruttivi
Non essendovi evidenti problemi, valutiamo la significatività degli effetti nel modello, analogamente a quanto abbiamo fatto nel caso dell’ANOVA a blocchi randomizzati. L’unica differenza sta nel fatto che, nei disegni a quadrato latino, vi sono tre effetti da testare, anche se l’unico ad avere una certa rilevanza è l’effetto del metodo di lavoro.
anova(mod)
## Analysis of Variance Table
##
## Response: Time
## Df Sum Sq Mean Sq F value Pr(>F)
## Method 3 145.69 48.563 12.7377 0.0051808 **
## Technician 3 17.19 5.729 1.5027 0.3065491
## Shift 3 467.19 155.729 40.8470 0.0002185 ***
## Residuals 6 22.87 3.812
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vediamo che esiste una differenza significativa tra i metodi e l’ipotesi nulla può essere rifiutata con una bassissima probabilità di errore di prima specie.
Ovviamente, dopo aver eseguito un’ANOVA a blocchi randomizzati o a quadrato latino, andremo eventualmente ad eseguire un test di confronto multiplo, seguendo le raccomandazioni esposte nel capitolo precedente. Anche questa parte ve la lasciamo per esercizio.