Capitolo 4 Modelli statistici ed analisi dei dati
L’eredità galileiana ci porta ad immaginare che il funzionamento della natura sia basato su una serie di relazioni causa-effetto, descrivibili utilizzando il linguaggio universale della matematica. La conoscenza esatta di queste relazioni, nella teoria, ci potrebbe consentire di prevedere l’andamento di ogni fenomeno naturale, almeno quelli osservabili con sufficiente precisione.
In effetti era proprio questa l’ambizione più grande degli scienziati all’inizio dell’ottocento: conoscendo lo stato iniziale di un sistema, doveva essere possibile prevederne con precisione l’evoluzione futura. Laplace diceva: “Possiamo considerare lo stato attuale dell’universo come l’effetto del suo passato e la causa del suo futuro. Un intelletto che ad un determinato istante dovesse conoscere tutte le forze che mettono in moto la natura, e tutte le posizioni di tutti gli oggetti di cui la natura è composta, se questo intelletto fosse inoltre sufficientemente ampio da sottoporre questi dati ad analisi, esso racchiuderebbe in un’unica formula i movimenti dei corpi più grandi dell’universo e quelli degli atomi più piccoli; per un tale intelletto nulla sarebbe incerto ed il futuro proprio come il passato sarebbe evidente davanti ai suoi occhi”. In realtà si è ben presto scoperto che si trattava di un’ambizione irrealistica, non tanto e non solo per la comparsa della meccanica quantistica un secolo dopo, ma anche per l’aumento di importanza degli studi in ambito psichiatrico e medico/biologico. Questi studi, infatti, venivano (e vengono) eseguiti su organismi viventi molto complessi, che, se sottoposti allo stesso stimolo, davano risposte altamente variabili e, spesso, anche difficilmente misurabili e controllabili.
Queste difficoltà fecero prevalere, tra i biologi, la convinzione che la natura funzionasse in base a meccanismi deterministici ben definiti, anche se difficilmente osservabili nella pratica sperimentale, a causa dei numerosi elementi d’incertezza che si manifestavano nel corso delle osservazioni sperimentali. Insomma, la natura è perfetta, ma l’osservazione è fallace, perché influenzata dalla presenza di una forte componente stocastica ed imprevedibile, che va sotto il nome generico di errore sperimentale. Di questo abbiamo già parlato nei capitoli precedenti. Abbiamo anche visto che Ronald Fisher, nel suo famoso testo “Il disegno degli esperimenti” ha posto le basi per una corretta metodica sperimentale, finalizzata a minimizzare l’impatto della componente stocastica e, soprattutto, ad impedire che essa si confondesse con gli effetti degli stimoli sperimentali in studio.
Minimizzare, tuttavia, non significa eliminare ed è evidente che, pur con tutti gli sforzi possibili, è impossibile evitare che i risultati sperimentali siano influenzati, sempre e comunque, da una certa quota di variabilità stocastica. Si vengono quindi a creare due contrapposte situazioni:
- la verità ‘vera’, immanente, che ‘agisce’ in base a meccanismi deterministici causa-effetto ben definiti.
- La ‘verità’ sperimentale, che si produce a partire dalla verità ‘vera’, per effetto dell’azione di elementi perturbativi casuali, che non ci permettono di osservare la verità ‘vera’.
Di conseguenza, la descrizione di qualunque risultato sperimentale non può essere realistica se non utilizzando un modello in grado di considerare contemporaneamente sia i nessi causa-effetto, che le altre forze ignote e, almeno apparentemente, di natura stocastica. I modelli matematici che incorporano anche effetti di natura casuale sono detti modelli statistici.
4.1 Verità ‘vera’ e modelli deterministici
In semplice linguaggio algebrico, possiamo porrescrivere un modello deterministico causa-effetto utilizzando una funzione di questo tipo:
\[ Y_E = f(X, \theta) \]
dove \(Y_E\) è l’effetto atteso dello stimolo \(X\), secondo la funzione \(f\), basata su una collezioni di parametri \(\theta\).
In questo modello vi sono una serie di componenti, che proviamo a guardare un po’ più nel dettaglio. La risposta attesa (\(Y_E\)) è l’oggetto del nostro studio e può assumere le forme più disparate: spesso è numerica, ma a volte rappresenta una qualità. In questo libro consideremo solo la situazione in cui \(Y_E\) è rappresentato da una sola variabile (analisi univariata), ma esistono casi in cui viene osservata ed analizzata la risposta di soggetti in relazione a molte variabili (analisi multivariata).
Lo stimolo sperimentale (\(X\)) è costituito da una o più variabili continue, discrete o categoriche, che rappresentano i trattamenti sperimentali. Insieme ad \(Y_E\), \(X\) è l’elemento noto di un esperimento, in quanto viene definito a priori con il disegno sperimentale.
La ‘funzione’ di risposta (\(f\)) è un’equazione, lineare o non-lineare, scelta in base a considerazioni di carattere biologico, o con un approccio puramente empirico, osservando l’andamento della curva di risposta.
I parametri di una funzione (\(\theta\)) sono un insieme di valori numerici che permettono di definire l’equazione di risposta.
Vediamo alcuni esempi.
Il modello più semplice è il cosiddetto modello della media:
\[ Y = \mu \]
Si tratta di una funzione identità, secondo la quale un’osservazione sperimentale dovrebbe conformarsi ad un certo valore atteso, come effetto di un unico stimolo sperimentale noto. Ha un solo parametro, cioè \(\mu\).
Un modello analogo, ma più complesso è il cosidetto modello ANOVA:
\[ Y = \left\{ {\begin{array}{ll} \mu_1 & se \quad X = A \\ \mu_2 & se \quad X = B \end{array}} \right. \]
In questo caso la risposta attesa dipende dallo stimolo sperimentale \(X\), che è composto di due trattamenti: se il soggetto è trattato con A, fornisce la risposta \(\mu_1\), se è trattato con B fornisce \(\mu_2\). Il trattamento sperimentale è costituito da una variabile categorica con due modalità e quindi abbiamo due parametri (\(\mu_1\) e \(\mu_2\)), ma l’estensione a più di due modalità è immediata.
Un ulteriore esempio di modello che vedremo in questo libro è la regressione lineare semplice, dove la relazione di risposta è descrivibile con una retta, la cui equazione generale è:
\[ Y = \beta_0 + \beta_1 \times X \]
In questo caso sia la \(Y\) che la \(X\) sono variabili quantitative e vi sono due parametri \(\beta_0\) e \(\beta_1\).
I modelli finora descritti sono lineari, ma esistono numerose funzioni che descrivono relazioni curvilinee, come, ad esempio, la parabola:
\[ Y = \beta_0 + \beta_1 \, X + \beta_2 \, X^2\]
caratterizzata da tre parametri, oppure la funzione esponenziale:
\[ Y = \beta_0 \, e^{\beta_1 X} \]
caratterizzata da due parametri (\(\beta_0\) e \(\beta_1\)), mentre \(e\) è l’operatore di Nepero. Delle funzioni curvilinee parleremo al termine di questo libro.
4.2 Genesi deterministica delle osservazioni sperimentali
Le equazioni esposte più sopra sono tutte nella loro forma generale e non sono utilizzabili se ai parametri non viene sostituito un valore numerico. E’proprio questo il nostro punto di partenza: un fenomeno scientifico può essere descritto attraverso un’equazione, nella quale ogni parametro assume un valore numerico specifico.
Facciamo un esempio: un pozzo è inquinato e contiene esattamente 120 \(mg/L\) di una sostanza erbicida. Pertanto, se facciamo un esperimento è preleviamo un’aliquota d’acqua da quel pozzo, determinando la concentrazione di erbicida, dovremmo ottenere un valore pari a 120 \(mg/L\). Utilizzando il modello della media, questo concetto si può esprimere come: \(Y_E = 120\); in questo caso \(f\) è la funzione identità e \(\theta = \mu = 120\).
Innalzando leggermente il livello di complessità, potremmo immaginare che la risposta produttiva (Y) del frumento dipenda dalla dose della concimazione azotata (X), seguendo un andamento lineare, con \(\beta_0 = 25\) e \(\beta_1 = 0.15\). Rifacendosi alla notazione esposta sopra, diremo che \(f\) è una retta e \(\theta = [25, 0.15]\). Di conseguenza, un eventuale esperimento di concimazione azotata, in assenza di qualunque fattore perturbativo, dovrebbe dare risultati assolutamento prevedili, come mostrato nel box sottostante, considerando livelli di concimazione pari a 0, 60, 120 e 180 kg/ha di azoto per ettaro.
Qualcuno potrebbe obiettare che si tratta di una situazione irrealistica, perché la relazione tra concimazione azotata e produzione del frumento non è lineare. Non importa; in questo momento vogliamo semplicemente illustrare qual è la genesi delle osservazioni sperimentali. Fondamentalmente postuliamo l’esistenza di un modello matematico deterministico (causa-effetto) che, in assenza di errore sperimentale, è in grado di descrivere il comportamento della natura in una data situazione pedo-climatica.
4.3 Errore sperimentale e modelli stocastici
In pratica, le risposte attese sono impossibili da riscontrare; infatti, l’errore sperimentale, puramente stocastico, confonde le nostre osservazioni e le rende diverse da quanto previsto dal modello deterministico. Come fare per incorporare questi effetti stocastici in un modello matematico?
Continuiamo a considerare l’esempio precedente, relativo al pozzo inquinato con un erbicida e caratterizzato da una concentrazione pari a 120 \(mg/L\). Anche se un qualunque campione di acqua analizzata con un gas-cromatografo dovrebbe restituire una misura pari esattamente a 120 \(mg/L\), ci rendiamo conto che, nella pratica, è molto probabile che questo non accada. Infatti, lo strumento è comunque caratterizzato da una sua imprecisione di misura che, per quanto piccola, fa si che ogni campione di acqua \(i\) restituisca una concentrazione diversa da quella degli altri campioni eventualmente analizzati. Quindi non osserveremo esattamente \(Y_E = 120\), ma, al suo posto, osserveremo \(Y_O \neq Y_E\), o meglio \(Y_O = 120 + \varepsilon\), dove \(\varepsilon\) è appunto una misura della componente stocastica individuale che distorce i risultati ogni volta che ripetiamo la misura.
Ci chiediamo: che valori potrebbe assumere \(\varepsilon\)? I valori individuali esatti non possiamo prevederli perchè sono frutto di errori casuali. Ma possiamo fare alcune considerazioni probabilistiche: se il valore atteso è 120, trovare concentrazioni comprese tra 119 e 121 (quindi \(\varepsilon = \pm 1\)) dovrebbe essere molto più frequente che non trovare concentrazioni pari a 40 \(mg/L\) o 200 \(mg/L\) (\(\varepsilon = \pm 80\)). In generale, trovare valori di \(\varepsilon\) vicini allo 0 dovrebbe essere molto più probabile che non trovarli lontani.
Insomma, anche se non siamo in grado di prevedere con esattezza \(\varepsilon\) per ogni misura che andremo a fare, potremmo pensare di utilizzare una funzione che restituisca la probabilità di ottenere una certa risposta, piuttosto che un’altra. Potremmo quindi pensare di modellizzare l’elemento stocastico con una funzione di probabilità.
4.3.1 Funzioni di probabilità
Se avessimo rilevato una qualità del soggetto, come il sesso (M/F), la mortalità (vivo/morto), la germinabilità (germinato/non germinato), avremmo una variabile categorica nominale e potremmo calcolare le probabilità definita come rapporto tra il numero degli eventi favorevoli e il numero totale di eventi possibili (probabilità ‘frequentista’).
Ad esempio, immaginiamo di aver rilevato il numero di germogli ‘laterali’ di accestimento di 20 piante di frumento e di averne trovate 4 con 0 germogli, 6 con 1 germoglio, 8 con due germogli e 2 con tre germogli. La funzione che assegna la probabilità P ad ognuno dei quattro eventi Y possibili (funzione di probabilità) è:
\[ P(Y) = \left\{ \begin{array}{l} 4/20 = 0.2 \,\,\,\,\,\,se\,\,\,\,\,\,Y = 0 \\ 6/20 = 0.3 \,\,\,\,\,\,se\,\,\,\,\,\,Y = 1 \\ 8/20 = 0.4\,\,\,\,\,\,se\,\,\,\,\,\, Y = 2 \\ 2/20 = 0.1 \,\,\,\,\,\,se\,\,\,\,\,\,Y = 3 \\ \end{array} \right. \]
Viene ad essere definita una distribuzione di probabilità, che ha due caratteristiche importanti:
- P(Y) è sempre non-negativo (ovvio! le probabilità sono solo positive o uguali a 0);
- la somma delle probabilità di tutti gli eventi è sempre pari ad 1 (ovvio anche questo: la probabilità che capiti uno qualunque degli eventi è sempre 1).
Se gli eventi possibili sono ordinabili (come nel caso precedente), oltre alla funzione di probabilità, si può definire anche la funzione di probabilità cumulata, detta anche funzione di ripartizione, con la quale si assegna ad ogni evento la sua probabilità più quella di tutti gli eventi ‘inferiori’. Nell’esempio precedente:
\[ P(Y) = \left\{ \begin{array}{l} 0.2\,\,\,\,\,\,se\,\,\,\,\,\,Y \leq 0 \\ 0.5\,\,\,\,\,\,se\,\,\,\,\,\,Y \leq 1 \\ 0.9\,\,\,\,\,\,se\,\,\,\,\,\,Y \leq 2 \\ 1.0\,\,\,\,\,\,se\,\,\,\,\,\,Y \leq 3 \\ \end{array} \right. \]
Per una distribuzione di probabilità come questa (classi numeriche ordinate), considerando il valore centrale di ogni classe, possiamo calcolare la media (valore atteso) come:
\[ \mu = E(Y) = \sum{\left[ y_i \cdot P(Y = y_i ) \right]} \]
e la varianza come:
\[\sigma ^2 = Var(Y) = E\left[ {Y - E(Y)} \right]^2 = \sum{ \left[ {\left( {y_i - \mu } \right)^2 \cdot P(Y = y_i )} \right]}\]
In questo caso specifico, la media è pari a:
e la varianza è pari a:
Mediamente, le nostre piante hanno 1.4 germogli con una varianza pari a 0.84.
4.3.2 Funzioni di densità
Ciò che abbiamo detto finora non si applica al nostro caso, in quanto abbiamo rilevato una variabile continua (concentrazione) e non abbiamo intenzione di discretizzarla in classi. In teoria, misure ripetute di concentrazione possono portare ad un numero di valori pressoché infinito e non ha molto senso chiedersi, ad esempio, qual è la probabilità di trovare una concentrazione esattamente pari a 120 \(mg/L\) (e non 120.0000001, o 119.99999). Capiamo da soli che questa probabilità è infinitesima.
Al contrario, potremmo pensare di calcolare la probabilità di ottenere un valore compreso in un intervallo, per esempio da 119 a 121 \(mg/L\), anche se questa operazione porterebbe all’introduzione di un elemento arbitrario, cioè l’ampiezza dell’intervallo prescelto. Possiamo tuttavia pensare di calcolare la densità di probabilità, vale a dire il rapporto tra la probabilità di un intervallo e la sua ampiezza (cioè la probabilità per unità di ampiezza dell’intervallo; per questo si parla di densità). Ora, se immaginiamo di restringere l’intervallo fino a farlo diventare infinitamente piccolo, anche la probabilità tende a diventare infinitesima con la stessa ‘velocità’, in modo che la densità di probabilità di un singolo valore di concentrazione tende ad un numero finito (ricordate il limite del rapporto di polinomi?).
Insomma, con i fenomeni continui non possiamo calcolare la probabilità dei singoli eventi puntiformi, ma possiamo calcolare la loro densità di probabilità e definire quindi apposite funzioni di densità. Analogamente alle funzioni di probabilità, le funzioni di densità debbono avere due caratteristiche:
- assumere solo valori non-negativi;
- la somma delle probabilità di tutti gli eventi possibili, calcolabile come integrale della funzione di densità, deve essere unitaria (anche in questo caso la densità di probabilità di tutti gli eventi possibili è pari ad 1).
Data una funzione di densità, possiamo costruire la corrispondente funzione di probabilità cumulata, facendo l’integrale per ogni evento pari o inferiore a quello dato (esempio: probabilità di trovare concentrazioni inferiori a 120 \(mg/L\)). Più in generale, per variabili continue sia la funzione di ripartizione (probabilità cumulata), che la media o la devianza sono definite ricorrendo agli integrali:
\[ \begin{array}{l} P(Y) = f(y) \\ P(Y \leq y) = \int\limits_{ - \infty }^y {f(y)} dy \\ \mu = E(Y) = \int\limits_{ - \infty }^{ + \infty } {yf(y)} dy \\ \sigma^2 = Var(Y) = \int\limits_{ - \infty }^{ + \infty } {\left( {y - \mu } \right)^2 f(y)} dy \\ \end{array}\]
In pratica, vedremo che, a seconda della funzione di densità, è possibile adottare formule semplificate per le diverse statistiche descrittive.
4.3.3 La distribuzione normale (curva di Gauss)
Torniamo ancora alla nostra popolazione di misure, relative alle concentrazioni di campioni di acqua prelevati dal pozzo inquinato. E’ ragionevole pensare che, effettuando le misurazioni con uno strumento sufficientemente preciso e in presenza delle sole variazioni casuali (visto che abbiamo idealmente rimosso ogni differenza sistematica spiegabile), i risultati tendono a differire tra di loro, muovendosi intorno ad un valor medio, rispetto al quale le misure superiori ed inferiori sono equiprobabili e tendono ad essere più rare, via via che ci si allontana dal valore medio. Questo ragionamento ci porta verso una densità di probabilità (parliamo di variabili continue) a forma di campana, che potrebbe essere descritta con una funzione continua detta curva di Gauss.
La curva è descritta dalla seguente funzione di densità:
\[P(Y) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left[{\frac{\left( {Y - \mu } \right)^2 }{2\sigma ^2 }} \right]\]
ove \(P(Y)\) è la densità di probabilità di una certa misura \(Y\), mentre \(\mu\) e \(\sigma\) sono rispettivamente la media e la deviazione standard della popolazione (per la dimostrazione si rimanda a testi specializzati). Le variabili casuali che possono essere descritte con la curva di Gauss, prendono il nome di variabili normali o normalmente distribuite.
Studiare le principali proprietà matematiche della curva di Gauss è estremamente utile. Ad esempio, senza voler entrare troppo nel dettaglio, guardando la curva di Gauss possiamo notare che:
- la forma della curva dipende da solo da \(\mu\) e \(\sigma\) (figura 4.1). Ciò significa che, se prendiamo un gruppo di individui e partiamo dal presupposto (assunzione parametrica) che in relazione ad un determinato carattere quantitativo (es. produzione) la distribuzione di frequenza è normale (e quindi può essere descritta con una curva di Gauss), allora basta conoscere la media e la deviazione standard degli individui e immediatamente conosciamo l’intera distribuzione di frequenza (cioè l’intera popolazione di misure);
- la curva ha due asintoti e tende a 0 quando x tende a infinito. Questo ci dice che se assumiamo che un fenomeno è descrivibile con una curva di Gauss, allora assumiamo che tutte le misure sono possibili, anche se la loro frequenza decresce man mano che ci si allontana dalla media;
- la probabilità che la x assuma valori compresi in un certo intervallo è data dall’integrale della curva di Gauss in quell’intervallo. Ad esempio, la figura 4.2 mostra l’80° percentile, cioè la misura più alta dell’80% delle misure possibili;
- Se la curva di Gauss è stata costruita utilizzando le frequenze relative, l’integrale della funzione è uguale ad 1. Infatti la somma delle frequenze relative di tutte le varianti possibili non può che essere uguale ad 1;
- la curva è simmetrica. Questo indica che la frequenza dei valori superiori alla media è esattamente uguale alla frequenza dei valori inferiori alla media.
- dato \(\sigma\), possiamo dire che la frequenza dei valori superiori a \(\mu + \sigma\) è pari al 15.87% ed è uguale alla frequenza dei valori inferiori a \(\mu - \sigma\).
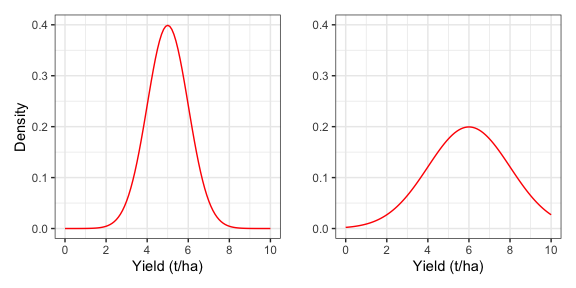
Figura 4.1: Distribuzioni normali con diversa media e deviazione standard (rispettivamente 5 e 1 a sinistra, 6 e 3 a destra

Figura 4.2: Integrale della curva di densità normale (80° percentile; sinistra) e curva di probabilità cumulata (destra)
4.4 Modelli ‘a due facce’
Teendo conto di quanto appena detto, possiamo modificare i nostri modelli per la descrizione dei risultati degli esperimenti in questo modo:
\[Y_i = f(X, \theta) + \varepsilon_i\]
introducendo l’elemento stocastico \(\varepsilon\) per descrivere l’ effetti casuali che subisce ogni soggetto \(i\). Globalmente, questi effetti vengono considerati come normalmente distribuiti, con media 0 e deviazione standard \(\sigma\):
\[ \varepsilon_i \sim N(0, \sigma) \]
Analogamente, possiamo scrivere:
\[Y_i \sim N[f(X, \theta), \sigma]\]
cioè che il valore osservato è normalmente distribuita con media che cambia in funzione dello stimolo \(X\) e deviazione standard \(\sigma\). Dato che si tratta di una semplice traslazione di una distribuzione normale lungo l’asse delle ascisse (come in figura 4.1), le due espressioni sono totalmente equivalenti.
Un modello di questo tipo (a due facce: deterministica + stocastica) ci consente la miglior descrizione di un qualunque fenomeno biologico: la parte deterministica ci consente di prevedere il risultato atteso, quella stocastica ci consente di capire quali osservazioni sono più probabili in pratica. Ad esempio, se ipotizziamo di misurare la concentrazione del nostro pozzo con uno strumento caratterizzato da \(\sigma = 12\), possiamo rispondere a tutte le seguenti domande
- Qual è la misura di concentrazione più probabile?
- Qual è la densità di probabilità di ottenere una concentrazione pari a 120 \(mg/L\)?
- Qual è la probabilità di ottenere una concentrazione inferiore a 110 \(mg/L\)?
- Qual è la probabilità di ottenere una concentrazione superiore a 130 \(mg/L\)?
- Qual è la probabilità di ottenere una concentrazione compresa tra 110 e 130 \(mg/L\)
- Quale concentrazione è superiore al 90% di tutte i valori ottenibili (90° percentile)?
- Quali sono quei due valori, simmetrici rispetto alla media e tali da formare un intervallo all’interno del quale cadono il 95% delle misure possibili?
La risposta alla prima domanda è banale (\(Y_E = 120\)), mentre per rispondere alle altre domande possiamo utilizzare le apposite funzioni di R. Per ogni distribuzione abbiamo a disposizione una funzione di densità (con prefisso ‘d’), una funzione di probabilità cumulata (con prefisso ‘p’) e una funzione inversa (prefisso ‘q’) che consente di calcolare i percentili. Nel caso della funzione gaussiana, abbiamo le funzioni dnorm(), pnorm() e qnorm(), che possiamo utilizzare per calcolare densità, probabilità e percentili, come indicato di seguito.
# Domanda 2
dnorm(120, mean = 120, sd = 12)
## [1] 0.03324519
# Domanda 3
pnorm(110, mean = 120, sd = 12)
## [1] 0.2023284Per la quarta domanda dobbiamo considerare che la funzione pnorm() fornisce la coda bassa della funzione, mentre dobbiamo individuare la coda alta (altezze maggiori della soglia data). Pertanto, abbiamo due possibili soluzioni, come indicato più sotto.
# Domanda 4
pnorm(130, mean = 120, sd = 12, lower.tail = F)
## [1] 0.2023284
1 - pnorm(130, mean = 120, sd = 12)
## [1] 0.2023284
# Domanda 5
pnorm(130, mean = 120, sd = 12) - pnorm(110, mean = 120, sd = 12)
## [1] 0.5953432
# Domanda 6
qnorm(0.9, mean = 120, sd = 12)
## [1] 135.3786
# Domanda 7
qnorm(0.025, mean = 120, sd = 12)
## [1] 96.48043
qnorm(0.975, mean = 120, sd = 12)
## [1] 143.51964.5 E allora?
Cerchiamo di ricapitolare. I risultati sperimentali sono un oggetto largamente ignoto e inconoscibile, perché sono, in parte, determinati in base a relazioni causa-effetto, ma, d’altra parte, essi sono puramente stocastici. Tuttavia è ragionevole supporre che essi seguano una qualche funzione di probabilità/densità (assunzione parametrica). Se questo è vero, allora possiamo utilizzare queste funzioni e i loro integrali per calcolare la probabilità di ottenere un certo risultato o un insieme di risultati.
4.6 Le simulazioni Monte Carlo
Guardandolo dal punto di vista che abbiamo appena illustrato, ogni esperimento scientifico non è altro che un’operazione di campionamento da una certa distribuzione di probabilità e questo campionamento può essere simulato impiegando un generatore di numeri casuali, con un procedimento che prende il nome di ‘metodo Monte Carlo’.
Prendiamo ancora il nostro pozzo inquinato e contenente 120 \(mg/L\) di un erbicida e immaginiamo di misurare la concentrazione di tre campioni d’acqua, utilizzando uno strumento caratterizzato da \(\sigma = 12\). I risultati di questo esperimento possono essere simulati:
- usando il modello deterministico per definire il valore atteso della produzione per ogni dose di azoto, che sarà la stessa per tutte le repliche (in questo caso \(Y_E = 120\));
- utilizzando un generatore gaussiano di numeri casuali, per simulare gli effetti stocastici, campionandoli da una distribuzione normale, con le caratteristiche desiderate.
set.seed(1234)
Y_E <- 120
epsilon <- rnorm(3, 0, 12)
Y_O <- Y_E + epsilon
Y_O
## [1] 105.5152 123.3292 133.0133La generazione di numeri casuali con il computer viene fatta attraverso algoritmi che, a partire da un seed iniziale, forniscono sequenze che obbediscono a certe proprietà fondamentali (numeri pseudo-casuali). Il comando set.seed(1234) ci permette di partire da un seed predefinito, in modo che, chiunque ripeta la simulazione con lo stesso seed, ottiene lo stesso risultato. Un’altra cosa da notare è che il nome della funzione che genera numeri casuali è formato dal nome della distribuzione (‘norm’) più il prefisso ‘r’. Questo è vero per tutte le altre distribuzioni in R (‘rbinom’, ‘rt’ e così via). Inoltre, il primo argomento definisce il numero di valori che vogliamo ottenere (tre, tanti quante sono le repliche).
La stessa strategia può essere utilizzata per simulare risultati sotto modelli deterministici più complessi: definisco i risultati attesi con il modello deterministico prescelto e ci aggiungo una componente casuale, campionandola da un distribuzione di probabilità/densità adeguata (usualmente gaussiana). Come ulteriore esempio possiamo considerare il codice sottostante, che può essere utilizzato per simulare un esperimento di concimazione azotata del frumento, con quattro dosi (0, 60, 120 e 180 kg/ha) e quattro repliche (sedici dati in totale).
set.seed(1234)
Dose <- rep(c(0, 60, 120, 180), each=4)
Yield_E <- 25 + 0.15 * Dose
epsilon <- rnorm(16, 0, 2.5)
Yield <- Yield_E + epsilon
dataset <- data.frame(Dose, Yield)
dataset
## Dose Yield
## 1 0 21.98234
## 2 0 25.69357
## 3 0 27.71110
## 4 0 19.13576
## 5 60 35.07281
## 6 60 35.26514
## 7 60 32.56315
## 8 60 32.63342
## 9 120 41.58887
## 10 120 40.77491
## 11 120 41.80702
## 12 120 40.50403
## 13 180 50.05937
## 14 180 52.16115
## 15 180 54.39874
## 16 180 51.724294.7 Analisi dei dati e ‘model fitting’
Nelle simulazioni sovrastanti abbiamo ipotizzato di conoscere il meccanismo di base che ha generato le nostre osservazioni sperimentali. In particolare, considerando il modello \(Y = f(X, \theta)\) abbiamo ipotizzato di conoscere \(f\), \(X\) e \(\theta\) ed abbiamo simulato \(Y\).
Nella realtà, noi non conosciamo i meccanismi che governano i fenomeni naturali ed è proprio per questo che facciamo esperimenti. Di conseguenza noi conosciamo \(X\) (stimolo sperimentale) ed \(Y\), ma ignoriamo \(f\) e \(\theta\). L’aspetto interessante è che l’ipotesi scientifica che sta alla base di un esperimento può essere posta sotto forma di modello matematico \(f\) e i risultati sperimentali possono essere utilizzati per determinare \(\theta\), con una tecnica definita model fitting.
Le diverse tecniche di analisi dei dati che descriveremo nei capitoli successivi sono accomunate dall’essere appunto tecniche di model fitting. Vedremo anche come queste tecniche possono essere utilizzate per verificare che le osservazioni sperimentali si conformino ad un dato modello (goodness of fit) oppure per confrontare due ipotesi alternative poste sotto forma di modelli diversi (model comparison).
4.8 Modelli stocastici non-normali
In questo capitolo abbiamo utilizzato un solo modello stocastico, cioè la funzione di densità gaussiana. Oltre a questa, che è largamente la più importante, esistono molti altri modelli stocastici, sia per eventi continui che discreti. La trattazione dei modelli stocastici non-normali esula dagli obiettivi di questo testo; chi fosse interessato, può trovare abbondanti informazioni in letteratura e, in particolare, nel primo dei riferimenti bibliografici forniti più sotto.