Capitolo 16 Appendice 3: Split-plot, split-block e altro
In questo libro abbiamo affrontato le questioni più rilevanti in relazione all’attività di ricerca e sperimentazione, quelle che dovrebbero far parte del bagaglio culturale di ogni laureato in discipline scientifiche. Tuttavia, è chiaro che la trattazione non è affatto esaustiva e quindi, se si avesse l’intenzioni di accostarsi al mondo della ricerca scientifica, non si potrebbe prescindere dalla lettura di altri testi di approfondimento, che sono stati via via segnalati. Tuttavia, mi sembra opportuno discutere alcuni modelli che sono estremamente diffusi nella sperimentazione di pieno campo, nella speranza che ciò possa essere utile nella pratica operativa.
16.1 Disegni a split-plot
Si parla di disegno a ‘split-plot’ (parcella suddivisa) quando un’unità sperimentale che ha subito (o è destinata a subire) un trattamento con il fattore sperimentale A, viene suddivisa in più sub-unità, alle quali vengono assegnati i diversi livelli di un altro fattore sperimentale (B), in modo randomizzato. Le sub-unità sperimentali non sono quindi indipendenti e viene a realizzarsi una sorta di raggruppamento tra di esse.
Nel disegno sperimentale a split-plot, le parcelle più grandi vengono definite ‘parcelle principlai’ (main-plots) e ad esse viene allocato il fattore sperimentale di I ordine. Le parcelle più piccole sono invece dette parcelle elementari (sub-plots) e ad esse viene allocato il fattore di II ordine.
Un disegno a split-plot può rendersi necessario per i seguenti motivi:
- un fattore sperimentale richiede parcelle più grandi dell’altro. Ad esempio, le lavorazioni del terreno, le irrigazioni o le epoche di semina, possono richiedere parcelle più grandi del diserbo, della concimazione o delle varietà. Di conseguenza si disegna l’esperimento per il fattore che richiede parcelle più grandi, che vengono poi suddivise per accomodare l’altro fattore sperimentale.
- Uno dei due fattori sperimentali è più ‘difficile’ da assegnare rispetto all’altro e quindi è preferibile manipolare congiuntamente tutto il gruppo di unità sperimentali che deve riceverlo. Ad esempio, se vogliamo misurare la resistenza alla corrosione di barre d’acciaio con diversi rivestimenti e forgiate a diverse temperature, è evidente che la gestione della temperatura nella fornace è piuttosto complessa, perchè richiede tempi lunghi per essere resettata e raggiungere un nuovo equilibrio. Invece che preparare una fornace per ogni rivestimento (manipolazione indipendente delle unità sperimentali), si mettono nella stessa fornace tutte le unità sperimentali con i diversi rivestimenti. Una situazione analoga si può avere se vogliamo provare diverse miscele per torte (con vari ingredienti), e diversi tempi di cottura; dato che non è agevole preparare una miscela diversa per ogni tempo di cottura, potremmo preferire di preparare una miscela tutta insieme, per poi suddividerla tra i diversi tempi di cottura.
- La disponibilità di unità sperimentali è limitata, come accade con gli armadi climatici, che vengono settati a diversa temperatura e all’interno delle quali vengono randomizzate le tesi sperimentali di secondo ordine.
16.1.1 Il caso-studio
Consideriamo l’esempio presentato nel capitolo 11, nel quale avevamo due fattori sperimentali a confronto: il diserbo, con due livelli (totale o localizzato sulla fila) e la lavorazione, con tre livelli (aratura profonda, aratura superficiale e minimum tillage). In quel capitolo abbiamo presentato l’esperimento come un fattoriale a blocchi randomizzati, la cui mappa di campo è stata riportata in Figura 11.2.
In realtà, questo esperimento non era stato pianificato come indicato in Figura 11.2, in quanto questo lay-out ci avrebbe costretto a lasciare parecchio spazio tra una parcella e l’altra, per poter manovrare con la macchina per la lavorazione del terreno. Per questo motivo, l’esperimento era stato disegnato a split-plot, in modo da raggruppare le parcelle caratterizzate dalla stessa lavorazione e quindi lavorare su superfici più ampie, lasciando inalterata la dimensione della parcella elementare. La reale mappa di campo è riportata in Figura 16.1.
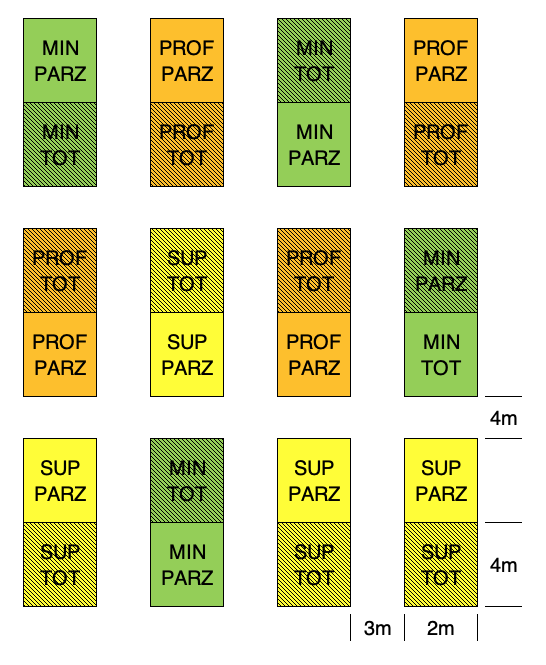
Figure 16.1: Schema sperimentale split-plot
Osservando la mappa dell’esperimento, possiamo fare le seguenti considerazioni.
- Lo split-plot introduce un vincolo alla randomizzazione, in quanto il fattore di II ordine non è randomizzato liberamente, ma la sua randomizzazione è vincolata al fatto che tutti i suoi livelli debbono essere inseriti nella stessa parcella principale.
- Ogni ‘main-plot’ funge da replica per le tesi di II ordine, ma non è vero il contrario. Ad esempio, se avessi un solo blocco, avrei tre repliche per il diserbo parziale e altrettante per il diserbo totale, ma avrei una e una sola replica per le levorazioni.
- Per quanto riguarda le lavorazioni, il disegno può essere assimilato ad un blocco randomizzato che trova la sua unità sperimentale (replica vera) nella main-plot, in quanto è ad essa che sono stati allocati i trattamenti in modo indipendente. Per le lavorazioni, le sub-plots si comportano da sub-repliche, in quanto non sono trattate con le lavorazioni in modo indipendente l’una dall’altra (mentre i diserbi sono stati allocati in modo indipendente alle sub-plots).
- La presenza delle main-plots non può mai essere dimenticata, in quanto essa da conto del fatto che due sub-parcelle nella stessa parcella principale sono più ‘simili’ di due sub-parcelle in due parcelle principali diverse. Insomma, se rimuoviamo la voce relativa alle parcelle principali rompiamo l’indipendenza degli errori sperimentali, venendo così a violare uno degli assunti fondamentali per l’ANOVA.
16.1.2 Definizione del modello lineare
Il modello ANOVA per un disegno a split-plot è simile a quello dell’ANOVA fattoriale, fatta salva la presenza di un effetto aggiuntivo, quello delle parcelle principali (main-plots), che costituiscono un elemento di raggruppamento delle osservazioni. Ad esempio, se una main-plot è più fertile di un’altra, tutte le osservazioni prese su questa main-plot saranno caratterizzate da un effetto positivo sulla produzione e, di conseguenza, saranno correlate tra di loro. In altre parole, la presenza di questo elemento comune, positivo o negativo che sia, rende le osservazioni prese su una main-plot più simili tra di loro che le osservazioni prese su main-plots diverse. Si parla, propriamente, di correlazione intra-classe, un concetto simile, ma non totalmente coincidente, con quello di correlazione di Pearson. E’evidente che l’effetto delle main-plots deve essere incluso nel modello, per evitare che finisca nel residuo e renda i residui correlati, cioè non indipendenti. Scriviamo quindi il modello:
\[Y_{ijk} = \mu + \gamma_k + \alpha_i + \theta_{ik} + \beta_j + \alpha\beta_{ij} + \varepsilon_{ijk}\]
dove \(\gamma\) è l’effetto del blocco \(k\), \(\alpha\) è l’effetto della lavorazione \(i\), \(\beta\) è l’effetto del diserbo \(j\), \(\alpha\beta\) è l’effetto dell’interazione per la specifica combinazione della lavorazione \(i\) e del diserbo \(j\). Abbiamo incluso anche \(\theta\) che è l’effetto della main-plot; dato che ogni parcella principale è identificata univocamente dal blocco \(k\) a cui appartiene e dalla lavorazione \(i\) in essa eseguita, abbiamo utilizzato i pedici corrispondenti.
Per la stima dei parametri, potremmo utilizzare il codice sottostante, anticipando però che è sbagliato, per i motivi che vedremo in seguito. Tuttavia, è importante notare che abbiamo definito le main-plots come combinazione tra Blocchi e Lavorazioni.
mainPlot <- factor(dataset$Lavorazione):factor(dataset$Blocco)
mod.wrong <- lm(Prod ~ factor(Blocco) + Lavorazione*Diserbo + mainPlot, data=dataset)16.1.3 La natura dell’effetto delle main-plots
Abbiamo anticipato che il modello sovrastante è sbagliato. Il probema è sia concettuale, che pratico. Da un punto di vista concettuale, noi abbiamo incluso le main-plots come un effetto fisso, al pari delle lavorazioni o del diserbo. In realtà c’è una grossa differenza: mentre i livelli delle lavorazioni e del diserbo li abbiamo attentamente prescelti, perché eravamo specificatamente interessati ad essi, nel caso delle main-plots non abbiamo nessun interesse specifico, le abbiamo selezionate come fossero le parcelle di un esperimento, in modo casuale da un universo più grosso, quello di tutte le main-plots possibili nel nostro appezzamento.
Insomma, stiamo dicendo che, mentre le lavorazioni ed il diserbo sono effetti cosiddetti fissi, le main-plots hanno un effetto di natura random: potremmo cambiarle a piacimento, senza che il nostro esperimento cambi o perda interesse. Cosa che non possiamo dire della lavorazione e del diserbo: se cambiamo i livelli inclusi nell’esperimento, cambia la finalità dello stesso.
Da un punto di vista pratico, se eseguiamo la scomposizione delle varianze con il modello sovrastante, tutti i test di F vengono effettuati utilizzando la varianza del residuo come denominatore. Tuttavia, per quanto riguarda le lavorazioni, i livelli sono stati allocati alle main-plots, non alle sub-plots e, pertanto, le repliche vere per questo fattore sperimentale sono le main-plots trattate con la stessa lavorazione, non le sub-plots. Ricordiamo che, secondo Fisher, l’errore sperimentale è definito come la variabilità tra repliche vere trattate allo stesso modo; di conseguenza, il residuo non è, e non può essere, la voce d’errore giusta per testare la significatività dell’effetto lavorazione.
Inoltre, se per un attimo immaginassimo di escludere il diserbo chimico e pensassimo di aver fatto un’unica misura per ogni main-plot, ci troveremmo di fronte ad un esperimento a blocchi randomizzati, nel quale le main-plots assumono il ruolo delle parcelle. In questo esperimento, l’errore residuo, sul quale testare la significatività dell’effetto della lavorazione, sarebbe dato proprio dalla devianza tra main-plots trattate allo stesso modo. Ovviamente, lo stesso approccio dovrebbe essere mantenuto in un esperimento a split-plot.
Insomma, in un esperimento a split-plot, oltre ad includere le main-plots nel modello per assicurare l’indipendenza dei residui, è anche necessario trattare l’effetto main-plots come un effetto random, sul quale testare la significatività dell’effetto del fattore di I ordine.
16.1.4 Scomposizione della varianza
I risultati ottenuti con questo esperimento sono disponibili nel file ‘beet.csv’, che può essere aperto direttamente da gitHub, con il codice sottostante.
path1 <- "https://raw.githubusercontent.com/OnofriAndreaPG/"
path2 <- "aomisc/master/data/"
name <- "beet.csv"
pathName <- paste(path1, path2, name, sep = "")
dataset <- read.csv(pathName, header=T)
head(dataset)
## Lavorazione Diserbo Blocco Prod
## 1 MIN tot 1 11.614
## 2 MIN tot 2 9.283
## 3 MIN tot 3 7.019
## 4 MIN tot 4 8.015
## 5 MIN parz 1 5.117
## 6 MIN parz 2 4.306Tutte le devianze sono uguali a quelle calcolate per un modello ANOVA a due vie. Rimane il problema di calcolare la devianza delle main-plots. Intuitivamente possiamo pensare di calcolarle attraverso la devianza delle medie ottenute in main-plots diverse. È giusto, ma è necessario ricordare che queste medie sono anche determinate dalla lavorazione che è stata eseguita in ciascuna main-plot e dal blocco di cui la main-plot fa parte. Pertanto, dalla devianza delle main-plots deve essere scorporata la devianza dei blocchi e quella delle lavorazioni.
Le produzioni medie in ogni main-plot sono:
medieMP <- tapply(dataset$Prod, mainPlot, mean)
medieMP
## MIN:1 MIN:2 MIN:3 MIN:4 PROF:1 PROF:2
## 8.3655 6.7945 7.9795 6.8160 10.7940 9.7275
## PROF:3 PROF:4 SUP:1 SUP:2 SUP:3 SUP:4
## 9.2470 9.9025 8.9970 8.5205 8.4470 9.2685La devianza, considerando che in ogni main-plot ci sono due osservazioni e considerando anche le devianze calcolate per l’ANOVA fattoriale a due vie, è quindi:
Questa devianza ha 6 gradi di libertà, in quanto abbiamo 12 main-plots, quindi 11 gradi di libertà, meno 2 gradi di libertà per le lavorazioni e tre gradi di libertà per i blocchi.
Per il resto, nulla cambia rispetto all’ANOVA fattoriale, salvo il fatto che il residuo è più piccolo ed ha meno gradi di libertà, in quanto da esso è stato scorporato l’effetto delle main-plots.
16.1.5 Il fitting con R
Il modello lineare per una disegno a split-plot ha due effetti random, cioè il residuo e l’effetto delle main-plots. Quando vi è più di un effetto random ed almeno un effetto fisso si parla di modelli misti (mixed models). In R ci sono molte funzioni per il fitting di questa classe di modelli, ma noi utilizzeremo la più semplice, anche se non necessariamente la più avanzata. Si tratta di ‘aov()’, nella quale l’effetto random delle main-plots viene immesso all’interno della funzione ‘Error()’ (notare la E maiuscola).
E’importante segnalare che la funzione ‘aov()’ fornisce risultati corretti solo quando il disegno è bilanciato, come in questo caso e in molti altricasi, nella sperimentazione agraria di pieno campo.
Il codice per il fitting è:
Le stime dei parametri non sono disponibili con questa funzione e la scomposizione della varianza può essere ottenuta con la funzione ‘anova()’ disponibile nel package ‘aomisc’, che deve essere installato e caricato. L’output presenta separatamente i due strati di errore, quello riferito alle main-plots e quello riferito alle sub-plots.
library(aomisc)
anova(mod.split)
##
## Error: mainPlot
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(Blocco) 3 3.660 1.22 2.001 0.2155
## Lavorazione 2 23.656 11.83 19.399 0.0024 **
## Residuals 6 3.658 0.61
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## Diserbo 1 3.32 3.320 1.225 0.2972
## Lavorazione:Diserbo 2 19.46 9.732 3.589 0.0714 .
## Residuals 9 24.40 2.711
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Confrontando il risultato dell’analisi a split-plot con quella dell’analisi fattoriale esposta in una lezione precedente possiamo notare che l’interazione lavorazione x diserbo non è più significativa, mentre lo era nel caso del disegno fattoriale semplice. E’evidente che i dati vanno elaborati seguendo il disegno sperimentale utilizzato per generarli, anche se ciò può diminuire la potenza dei test di F, per il più basso numero di gradi di libertà del residuo.
Medie e SEM
Le medie marginali attese si ottengono come al solito, tramite la funzione ‘emmeans()’
library(emmeans)
medieA <- emmeans(mod.split, ~Lavorazione)
## Note: re-fitting model with sum-to-zero contrasts
## NOTE: Results may be misleading due to involvement in interactions
medieB <- emmeans(mod.split, ~Diserbo)
## Note: re-fitting model with sum-to-zero contrasts
## NOTE: Results may be misleading due to involvement in interactions
medieAB <- emmeans(mod.split, ~Lavorazione:Diserbo)
## Note: re-fitting model with sum-to-zero contrasts
medieA; medieB; medieAB
## Lavorazione emmean SE df lower.CL upper.CL
## MIN 7.49 0.276 6 6.81 8.16
## PROF 9.92 0.276 6 9.24 10.59
## SUP 8.81 0.276 6 8.13 9.48
##
## Results are averaged over the levels of: Blocco, Diserbo
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
## Diserbo emmean SE df lower.CL upper.CL
## parz 8.37 0.372 12.6 7.56 9.17
## tot 9.11 0.372 12.6 8.30 9.92
##
## Results are averaged over the levels of: Blocco, Lavorazione
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
## Lavorazione Diserbo emmean SE df lower.CL
## MIN parz 6.00 0.644 12.6 4.60
## PROF parz 10.63 0.644 12.6 9.23
## SUP parz 8.48 0.644 12.6 7.08
## MIN tot 8.98 0.644 12.6 7.59
## PROF tot 9.21 0.644 12.6 7.81
## SUP tot 9.14 0.644 12.6 7.74
## upper.CL
## 7.39
## 12.03
## 9.87
## 10.38
## 10.60
## 10.54
##
## Results are averaged over the levels of: Blocco
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95Gli errori standard si calcolano in modo più complicato che non nel caso dell’ANOVA fattoriale semplice. Infatti, oltre che al numero di repliche degli effetti in gioco, è necessario fare attenzione alla scelta della voce d’errore. In generale, il calcolo degli errori standard non è banale, in quanto dobbiamo tener presenti le componenti di varianza che agiscono su ogni strato di errore. Le formule da impiegare sono riportate più sotto; A è il fattore principale (lavorazione), B il fattore secondario (diserbo), \(r\) il numero di repliche, \(a\) il numero di livelli di A e \(b\) il numero di livelli di B, MSE(1) è l’errore delle main-plots ed MSE(2) è il residuo:
\[SEM_A = \sqrt{\frac{MSE(1)}{r b}} = \sqrt{\frac{0.61}{4 \times 2}} = 0.276\]
\[SEM_B = \sqrt{\frac{(b - 1) MSE(2) + MSE(1)}{r a b}} = \sqrt{ \frac{(2 - 1) \times 2.711 + 0.61}{4 \times 3 \times 2}} = 0.372\]
\[SEM_{A:B} = \sqrt{\frac{[(b - 1) MSE(2) + MSE(1)]}{r b}} = \sqrt{ \frac{(2 - 1) \times 2.711 + 0.61}{4 \times 2}} = 0.644\]
I SEMs vengono utilizzati come misura di variabilità per le medie del primo fattore sperimentale, del secondo fattore sperimentale e delle combinazioni tra i due fattori sperimentali.
Bisogna tener presente che, a parte il fattore sperimentale di primo livello, per le altre medie i SEM sono costruiti operando una combinazione lineare di varianze. Pertanto, il numero di gradi di libertà potrà essere solo approssimato, come vedremo in seguito.
16.1.6 SED e confronti multipli
Nei disegni a split-plot abbiamo 4 tipi di differenze tra medie.
- Differenze tra due medie del fattore principale A (per esempio tra MIN - SUP)
- Differenze tra due medie del fattore B (TOT - PARZ)
- Differenze tra due medie del fattore B per lo stesso livello di A (MIN:TOT - MIN:PARZ). Per questa situazione si parla di differenze tra B entro A, che si abbrevia B|A.
- Differenze tra due medie del fattore B per un diverso livello di A (MIN:TOT - SUP:PARZ). In questo caso l’abbreviazione è B:A.
Per ognuna di queste differenza vi è una voce di errore (Errore standard della differenza = SED), ottenuto con il termine appropriato nell’ANOVA.
\[SED_A = \sqrt{\frac{2 \times MSE(1)}{r b}}\]
\[SED_B = \sqrt{\frac{2 \times MSE(2)}{r a}}\]
\[SED_{B|A} = \sqrt{\frac{2 \times MSE(2)}{r}}\]
\[SED_{A:B} = \sqrt{\frac{2 [(b - 1) MSE(2) + MSE(1)]}{r b}}\]
In questo caso, l’unico effetto significativo è quello relativo alla ‘lavorazione’, con un SED pari a:
\[SED_{LAV} = \sqrt {\frac{{2 \times 0.6097}}{{4 \times 2}}} = 0.3904\]
I SED sono utili per i test di confronto multiplo, che, tuttavia, possono essere eseguiti, come usuale, con R. In questo caso, solo l’effetto lavorazione è significativo, quindi operiamo il confronto multiplo per questo effetto.
multcomp::cld(medieA, Letters = LETTERS)
## Lavorazione emmean SE df lower.CL upper.CL .group
## MIN 7.49 0.276 6 6.81 8.16 A
## SUP 8.81 0.276 6 8.13 9.48 B
## PROF 9.92 0.276 6 9.24 10.59 B
##
## Results are averaged over the levels of: Blocco, Diserbo
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 3 estimates
## significance level used: alpha = 0.05Un aspetto da considerare, qualora l’interazione ‘A:B’ fosse significativa, è che se vogliamo confrontare tra di loro combinazioni in cui i livelli di A sono diversi (ad esempio la media ottenuta con le lavorazioni superficiali e il diserbo totale con quella ottenuta con la lavorazione profonda e il diserbo totale), dobbiamo tener presente che sono coivolti entrambi gli strati di errore (vedi le formule più sopra). In questo caso il SED è costruito come combinazione lineare di \(MSE(1)\) ed \(MSE(2)\) e il calcolo dei suoi gradi di libertà non è banale. In questo esempio, il SED è:
\[SED_{A:B} = \sqrt {\rm{2} \times \frac{{{\rm{(2 - 1)}} \times {\rm{2}}{\rm{.711 + 0}}{\rm{.6097}}}}{{4 \times 2}}}\]
La combinazione lineare tra varianze è della forma:
\[M = \alpha _1 MS(1) + \alpha _2 MS(2) = ({\rm{2 - 1}}) \times {\rm{2}}.{\rm{711 + 1}} \times {\rm{0}}.{\rm{6097}}\]
ed il numero di gradi di libertà per M (da utilizzare nel confronto multiplo) si può ottenere con l’approssimazione di Satterthwaite:
\[df_M = \frac{{M^2 }}{{\sum\limits_{i = 1}^n {\frac{{\left( {\alpha _i MS_i } \right)^2 }}{{df_i }}} }} = \frac{{11.6097}}{{\frac{{({\rm{2 - 1}}) \times {\rm{2}}.{\rm{711}}}}{6} + \frac{{0.6097}}{9}}} = 12.554\]
dove df sta per ‘degrees of freedom’ (gradi di libertà) relativi ad ognuna delle varianze in gioco.
multcomp::cld(medieAB, Letters = LETTERS)
## Lavorazione Diserbo emmean SE df lower.CL
## MIN parz 6.00 0.644 12.6 4.60
## SUP parz 8.48 0.644 12.6 7.08
## MIN tot 8.98 0.644 12.6 7.59
## SUP tot 9.14 0.644 12.6 7.74
## PROF tot 9.21 0.644 12.6 7.81
## PROF parz 10.63 0.644 12.6 9.23
## upper.CL .group
## 7.39 A
## 9.87 AB
## 10.38 AB
## 10.54 B
## 10.60 B
## 12.03 B
##
## Results are averaged over the levels of: Blocco
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 6 estimates
## significance level used: alpha = 0.0516.2 Disegni a split-block
In alcune circostanze, soprattutto nelle prove di diserbo chimico, potrebbe trovare applicazione un altro tipo di schema sperimentale, nel quale ogni blocco viene diviso in tante righe quanti sono i livelli di un fattore sperimentale e tante colonne quanti sono i livelli dell’altro. In questo modo, il primo trattamento sperimentale viene applicato a tutte le parcelle di una riga e l’altro trattamento a tutte le parcelle di una colonna. Ovviamente, l’allocazione alle righe e alle colonne è casuale e cambia in ogni blocco.
Questo disegno è detto strip-plot ed è molto comodo perché consente di lavorare velocemente. Se consideriamo il caso studio precedente, un disegno a strip-plot potrebbe essere immaginato come in Figura 16.2.
Figure 16.2: Esempio di un disegno a strip-plot per il dataset ‘beet.csv’, che prevede tre livelli di lavorazione e due livelli di diserbo chimico
16.2.1 Definizione del modello lineare
Dalla mappa si può osservare che, entro ogni blocco, le osservazioni sono raggruppate per riga e per colonna. Di conseguenza, anche le righe e le colonne debbono essere incluse nel modello lineare, per ripristinare l’indipendenza dei residui. Il modello è quindi:
\[Y_{ijk} = \mu + \gamma_k + \alpha_i + \theta_{ik} + \beta_j + \zeta_{jk} + \alpha\beta_{ij} + \varepsilon_{ijk}\]
Analogamente a quanto abbiamo visto per lo split-plot, le 12 righe sono univocamente definite da un livello di lavorazione e un blocco e, per questo, l’effetto \(\theta\) porta i pedici \(i\) e \(k\). D’altra parte, le 8 colonne sono definite da un livello di diserbo e un blocco, per cui l’effetto \(\zeta\) porta i pedici \(j\) e \(k\). Entrambi gli effetti sono da considerare random, per cui anche questo è un modello ‘misto’, con tre effetti random.
16.2.2 Scomposizione della varianza
L’effetto delle righe e delle colonne può essere stimato come l’effetto delle main-plots nel disegno a split-plot. Per i tst F, dobbiamo considerare che, per entrambi i fattori sperimentali, il disegno può essere assimilato ad un blocco randomizzato e, di conseguenza, l’effetto delle lavorazioni dovrebbe essere saggiato sull’effetto delle righe, mentre l’effetto del diserbo su quello delle colonne.
Per la scomposizione della varianza utilizziamo R e la funzione ‘aov()’, con il codice è esposto di seguito; come nel caso precedente, è opportuno creare una variabile aggiuntiva che, in questo caso, codifica per le main-plots relative al diserbo chimico.
mainPlot2 <- with(dataset, factor(Blocco):factor(Diserbo))
model.strip <- aov(Prod ~ factor(Blocco) + Lavorazione*Diserbo +
Error(mainPlot + mainPlot2), data = dataset)
## Warning in aov(Prod ~ factor(Blocco) + Lavorazione *
## Diserbo + Error(mainPlot + : Error() model is singular
anova(model.strip)
##
## Error: mainPlot
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(Blocco) 3 3.660 1.22 2.001 0.2155
## Lavorazione 2 23.656 11.83 19.399 0.0024 **
## Residuals 6 3.658 0.61
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Error: mainPlot2
## Df Sum Sq Mean Sq F value Pr(>F)
## Diserbo 1 3.32 3.32 0.988 0.393
## Residuals 3 10.08 3.36
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## Lavorazione:Diserbo 2 19.46 9.732 4.077 0.0762 .
## Residuals 6 14.32 2.387
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1SED e confronti multipli
Si opera nel modo usuale. In questa sede, come riferimento, riportiamo solo le formule per il calcolo dei SED.
\[SED_A = \sqrt{2 \times \frac{MSE(1)}{rb}}\] \[SED_B = \sqrt{2 \times \frac{MSE(2)}{ra}}\]
\[SED_{A|B} = \sqrt{2 \times \frac{\left(b-1\right) MSE(3) + MSE(1)}{rb}}\]
\[SED_{B|A} = \sqrt{2 \times \frac{\left(a-1\right) MSE(3) + MSE(2)}{ra}}\]
\[SED_{A:B} = \sqrt{2 \times \frac{\left(ab - a-b\right) MSE(3) + b \, MSE(2) + a \, MSE(1)}{rab}}\]
16.3 Disegni gerarchici
Nel capitolo 11 (e negli esempi sovrastanti) abbiamo presentato un esperimento fattoriale ‘incrociato’ (crossed), nel quale i livelli di A sono gli stessi per ogni livello di B (e viceversa). In alcune situazioni, i disegni fattoriali possono essere gerarchici (nested), cioè i livelli di un fattore cambiano al cambiare dei livelli dell’altro fattore.
Ad esempio, potremmo prendere tre linee pure impollinanti di mais (A1, A2 e A3) e incrociarle con tre linee portaseme, diverse per ogni linea impollinante (B1, B2 e B3 incrociate con A1, B4, B5 e B6 incrociate con A2 e B7, B8 e B9 incrociate con A3). In questo modo verremmo a misurare le produzioni di 9 ibridi, divisi in tre gruppi, in base alle linee impollinanti. Se immaginiamo di impiantare in campo un esperimento del genere, utilizzando uno schema a blocchi randomizzati con quattro repliche, alla fine ci troviamo con 36 dati, come quelli riportati nel dataset ‘Crosses.csv’, che è disponibile su gitHub, e al solito, può essere caricato con il codice indicato di seguito.
path1 <- "https://raw.githubusercontent.com/OnofriAndreaPG/"
path2 <- "aomisc/master/data/"
name <- "Crosses.csv"
pathName <- paste(path1, path2, name, sep = "")
dataset <- read.csv(pathName, header=T)
head(dataset, 15)
## Male Female Block Yield
## 1 A1 B1 1 9.984718
## 2 A1 B1 2 13.932663
## 3 A1 B1 3 12.201312
## 4 A1 B1 4 1.916661
## 5 A1 B2 1 8.928465
## 6 A1 B2 2 10.513908
## 7 A1 B2 3 10.035964
## 8 A1 B2 4 2.375822
## 9 A1 B3 1 21.511028
## 10 A1 B3 2 21.859852
## 11 A1 B3 3 17.626284
## 12 A1 B3 4 13.966646
## 13 A2 B4 1 17.483089
## 14 A2 B4 2 19.480893
## 15 A2 B4 3 12.83879216.3.1 Definizione di un modello lineare
In un esperimento simile, abbiamo un effetto blocco (\(\gamma\)) e un effetto ‘paterno’ (\(\alpha\)). Invece, l’effetto ‘materno’ (\(\delta\)) può essere individuato solo entro ogni linea impollinante, dato che le linee portaseme sono diverse per ogni linea impollinante. In altre parole, l’effetto ‘materno’ è gerarchicamente inferiore all’effetto ‘paterno’, come evidenziato nella Figura 16.3.
Per descrivere il meccanismo di generazione delle osservazioni, possiamo utilizzare questo modello:
\[ Y_{ijk} = \mu + \gamma_k + \alpha_i + \delta_{ij} + \varepsilon_{ijk}\]
dove \(\gamma_k\) è l’effetto del blocco (con \(k\) che va da 1 a 4), \(\alpha_i\) è l’effetto dell’impollinante (con \(i\) che va da 1 a 3) e \(\delta_{ij}\) è l’effetto del portaseme (con \(j\) che va da 1 a 9) entro ogni impollinante \(i\). Ancora, \(\varepsilon\) è il residuo, assunto normalmente distribuito, con media zero e deviazione standard \(\sigma\) (omoscedasticità). Vediamo subito la principale differenza con un disegno fattoriale incrociato: mentre per quest’ultimo disegno il modello contiene i due fattori sperimentali A e B, insieme all’interazione A:B, nel modello per un disegno innestato abbiamo solo il fattore A ed il fattore B entro A (abbreviato come A/B), mentre manca l’effetto principale B, che, di fatto, non può esistere.

Figure 16.3: Struttura di un disegno sperimentale gerarchico
16.3.2 Stima dei parametri
Per la stima dei parametri, utilizziamo R ed il metodo dei minimi quadrati, attraverso l’ormai usuale funzione ‘lm()’.
model <- lm(Yield ~ factor(Block) + Male + Male:Female, data = dataset)
summary(model)
##
## Call:
## lm(formula = Yield ~ factor(Block) + Male + Male:Female, data = dataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.95836 -1.14888 0.04749 1.08992 2.64592
##
## Coefficients: (18 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.3625 0.9805 11.589 2.56e-11
## factor(Block)2 1.1476 0.8005 1.434 0.1646
## factor(Block)3 -1.2472 0.8005 -1.558 0.1323
## factor(Block)4 -7.3151 0.8005 -9.138 2.78e-09
## MaleA2 -0.7878 1.2008 -0.656 0.5180
## MaleA3 0.5975 1.2008 0.498 0.6233
## MaleA1:FemaleB2 -1.5453 1.2008 -1.287 0.2104
## MaleA2:FemaleB2 NA NA NA NA
## MaleA3:FemaleB2 NA NA NA NA
## MaleA1:FemaleB3 9.2321 1.2008 7.688 6.33e-08
## MaleA2:FemaleB3 NA NA NA NA
## MaleA3:FemaleB3 NA NA NA NA
## MaleA1:FemaleB4 NA NA NA NA
## MaleA2:FemaleB4 6.4599 1.2008 5.380 1.59e-05
## MaleA3:FemaleB4 NA NA NA NA
## MaleA1:FemaleB5 NA NA NA NA
## MaleA2:FemaleB5 2.5073 1.2008 2.088 0.0476
## MaleA3:FemaleB5 NA NA NA NA
## MaleA1:FemaleB6 NA NA NA NA
## MaleA2:FemaleB6 NA NA NA NA
## MaleA3:FemaleB6 NA NA NA NA
## MaleA1:FemaleB7 NA NA NA NA
## MaleA2:FemaleB7 NA NA NA NA
## MaleA3:FemaleB7 10.0089 1.2008 8.335 1.52e-08
## MaleA1:FemaleB8 NA NA NA NA
## MaleA2:FemaleB8 NA NA NA NA
## MaleA3:FemaleB8 7.6209 1.2008 6.346 1.46e-06
## MaleA1:FemaleB9 NA NA NA NA
## MaleA2:FemaleB9 NA NA NA NA
## MaleA3:FemaleB9 NA NA NA NA
##
## (Intercept) ***
## factor(Block)2
## factor(Block)3
## factor(Block)4 ***
## MaleA2
## MaleA3
## MaleA1:FemaleB2
## MaleA2:FemaleB2
## MaleA3:FemaleB2
## MaleA1:FemaleB3 ***
## MaleA2:FemaleB3
## MaleA3:FemaleB3
## MaleA1:FemaleB4
## MaleA2:FemaleB4 ***
## MaleA3:FemaleB4
## MaleA1:FemaleB5
## MaleA2:FemaleB5 *
## MaleA3:FemaleB5
## MaleA1:FemaleB6
## MaleA2:FemaleB6
## MaleA3:FemaleB6
## MaleA1:FemaleB7
## MaleA2:FemaleB7
## MaleA3:FemaleB7 ***
## MaleA1:FemaleB8
## MaleA2:FemaleB8
## MaleA3:FemaleB8 ***
## MaleA1:FemaleB9
## MaleA2:FemaleB9
## MaleA3:FemaleB9
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.698 on 24 degrees of freedom
## Multiple R-squared: 0.9405, Adjusted R-squared: 0.9132
## F-statistic: 34.48 on 11 and 24 DF, p-value: 5.236e-12Per chi volesse comprendere l’output ottenuto e il significato biologico dei parametri, ricordiamo che R impiega, di default, il vincolo sul trattamento. Di conseguenza, \(\alpha_1 = 0\) e \(\delta_{11} = 0\). Inoltre, visto che l’effetto materno deve essere definito per ogni impollinante, è necessario vincolare un valore di \(\delta\) per ogni impollinante. Da questo punto di vista, la soluzione adottata da R non è molto intuitiva, in quanto questo software vincola l’ultimo livello di B per ogni livello di A; quindi pone i vincoli \(\delta_{26}=0\) e \(\delta_{39} = 0\).
Con questi vincoli, \(\mu\) è il valore atteso per l’ibrido ottenuto dal primo impollinante, primo portaseme (A1B1) nel primo blocco. I parametri \(\gamma_k\) sono ottenuti analogamente a quanto illustrato nel capitolo sull’ANOVA fattoriale. Invece, i parametri \(\alpha_i\) debbono essere ottenuti in modo diverso, in quanto non possiamo cambiare l’impollinante mantenendo costante il portaseme. Possiamo notare che:
\[ \bar{Y}_{111} = \mu + \alpha_1 + \delta_{11} = \mu\]
e (per il vincolo imposto):
\[ \bar{Y}_{261} = \mu + \alpha_2 + \delta_{26} = \mu + \alpha_2\]
Quindi:
\[ \alpha_2 = \bar{Y}_{261} - \bar{Y}_{111}\]
e, analogamente:
\[ \alpha_3 = \bar{Y}_{291} - \bar{Y}_{111}\]
La stima di \(\delta_{ij}\) è più semplice, basta notare, ad esempio, che
\[ \bar{Y}_{121} = \mu + \alpha_1 + \delta_{12} = \mu + \delta_{12}\]
Quindi:
\[ \delta_{12} = \bar{Y}_{121} - \bar{Y}_{111}\]
e così via, per tutti gli altri parametri.
16.3.3 Scomposizione della varianza
Per suddividere la devianza totale delle osservazioni nelle quote che competono ad ogni effetto, utilizziamo il solito metodo sequenziale. La devianza totale è ottenuto da un modello nullo, calcolando la somma dei quadrati degli scarti:
Inseriamo ora il blocco, calcoliamo la devianza del residuo e, per sottrazione, otteniamo la devianza del blocco
modBl <- lm(Yield ~ factor(Block), data = dataset)
BlSS <- TSS - sum(residuals(modBl)^2)
BlSS
## [1] 383.7506Successivamente, inseriamo gli altri effetti, nello stesso modo.
modA <- lm(Yield ~ factor(Block) + Male, data = dataset)
ASS <- TSS - BlSS - sum(residuals(modA)^2)
ASS
## [1] 134.7567
BSS <- TSS - BlSS - ASS - sum(residuals(model)^2)
BSS
## [1] 575.1607I gradi di libertà, per gli effetti immessi in sequenza, sono, rispettivamente, 3 (abbiamo quattro blocchi), 2 (abbiamo tre ‘parentali’) e 6 (abbiamo calcolato gli scostamenti rispetto alle medie degli impollinanti: quindi abbiamo, 2 gradi di libertà per ogni impollinante).
Più facilmente, arriviamo agli stessi risultati con la funzione ’anova(), in R:
anova(model)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(Block) 3 383.75 127.917 44.355 6.051e-10 ***
## Male 2 134.76 67.378 23.363 2.331e-06 ***
## Male:Female 6 575.16 95.860 33.239 1.742e-10 ***
## Residuals 24 69.21 2.884
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 116.3.4 Medie e SEM
Il calcolo delle medie è banale, così come il calcolo degli errori standard. Dobbiamo solo ricordare che, per ogni parentale, vi sono 12 repliche (4 blocchi per 3 portaseme). Quindi
\[SEM_A = \sqrt{\frac{MSE}{r b}} = \sqrt{\frac{2.079}{4 \times 3}} = 0.416\]
Al contrario, per ognuno dei 9 portaseme abbiamo 4 repliche
\[SEM_B = \sqrt{\frac{MSE}{r}} = \sqrt{\frac{2.079}{4}} = 0.721\]
Più in generale, possiamo calcolare le medie marginali attese con la funzione ‘emmeans()’
library(emmeans)
medie <- emmeans(model, ~Male)
medie
## Male emmean SE df lower.CL upper.CL
## A1 12.1 0.49 24 11.1 13.1
## A2 11.7 0.49 24 10.7 12.7
## A3 16.0 0.49 24 15.0 17.0
##
## Results are averaged over the levels of: Block, Female
## Confidence level used: 0.95library(emmeans)
medie <- emmeans(model, ~Male:Female)
medie
## Female Male emmean SE df lower.CL upper.CL
## B1 A1 9.51 0.849 24 7.76 11.26
## B2 A1 7.96 0.849 24 6.21 9.72
## B3 A1 18.74 0.849 24 16.99 20.49
## B4 A2 15.18 0.849 24 13.43 16.93
## B5 A2 11.23 0.849 24 9.48 12.98
## B6 A2 8.72 0.849 24 6.97 10.47
## B7 A3 20.12 0.849 24 18.36 21.87
## B8 A3 17.73 0.849 24 15.97 19.48
## B9 A3 10.11 0.849 24 8.35 11.86
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95Se necessario, contrasti e confronti multipli possono essere eseguiti come usuale.
Volevo concludere precisando che, specificatamente per questo esempio, un plant breeder potrebbe non essere interessato a valutare la significatività degli effetti con il test F o ad effettuare confronti tra le medie, ma potrebbe essere più interessato a valutare la variabilità delle produzioni legata alle linee materne e/o paterne, per ottenere alcuni indicatori noti come ‘componenti di varianza’, che sono fondamentali per studiare l’ereditabilità dei caratteri. Di conseguenza, per un plant breeder, la tabella ANOVA non è il punto di arrivo, ma solo il punto di partenza per altre valutazioni. Per questo rimandiamo alla letteratura specialistica.