In this post, I am going to talk about an issue that is often overlooked by agronomists and biologists. The point is that field experiments are very often laid down in blocks, using split-plot designs, strip-plot designs or other types of designs with grouping factors (blocks, main-plots, sub-plots). We know that these grouping factors should be appropriately accounted for in data analyses: ‘analyze them as you have randomized them’ is a common saying attributed to Ronald Fisher. Indeed, observations in the same group are correlated, as they are more alike than observations in different groups. What happens if we neglect the grouping factors? We break the independence assumption and our inferences are invalid (Onofri et al., 2010).
To my experience, field scientists are totally aware of this issue when they deal with ANOVA-type models (e.g., see Jensen et al., 2018). However, a brief survey of literature shows that there is not the same awareness, when field scientists deal with linear/nonlinear regression models. Therefore, I decided to sit down and write this post, in the hope that it may be useful to obtain more reliable data analyses.
An example with linear regression
Let’s take a look at the ‘yieldDensity.csv’ dataset, that is available on gitHub. It represents an experiment where sunflower was tested with increasing weed densities (0, 14, 19, 28, 32, 38, 54, 82 plants per \(m^2\)), on a randomised complete block design, with 10 blocks. a swift plot shows that yield is linearly related to weed density, which calls for linear regression analysis.
rm(list=ls())
library(nlme)
library(lattice)
dataset <- read.csv("https://raw.githubusercontent.com/OnofriAndreaPG/agroBioData/master/yieldDensityB.csv",
header=T)
dataset$block <- factor(dataset$block)
head(dataset)
## block density yield
## 1 1 0 29.90
## 2 2 0 34.23
## 3 3 0 37.12
## 4 4 0 26.37
## 5 5 0 34.48
## 6 6 0 33.70
r
plot(yield ~ density, data = dataset)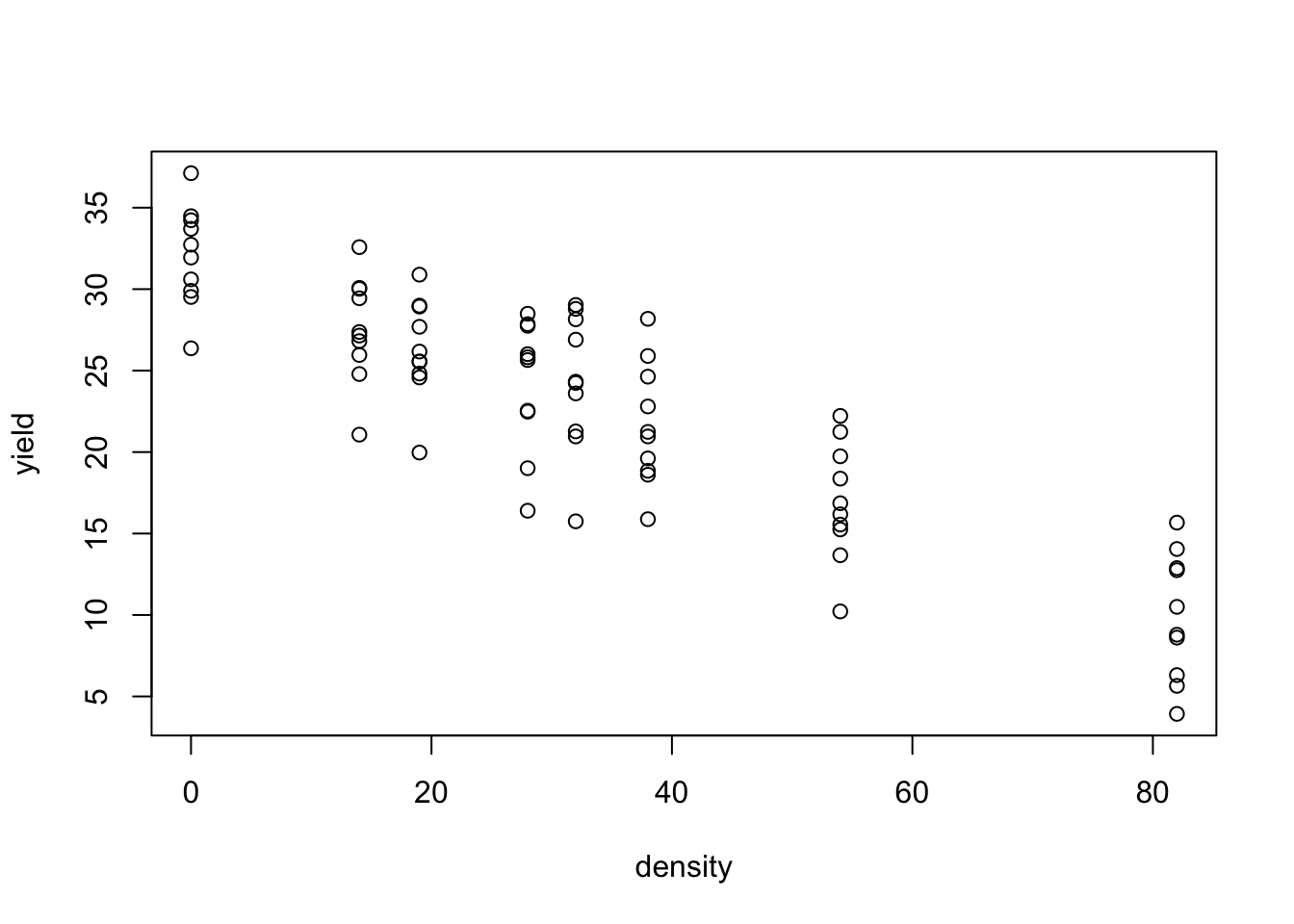
We might be tempted to neglect the block effect and run a linear regression analysis of yield against density. This is clearly wrong (I am violating the independence assumption) and inefficient, as any block-to-block variability goes into the residual error term, which is, therefore, inflated.
Some of my collegues would take the means for densities and use those to fit a linear regression model (two-steps analysis). By doing so, block-to-block variability is cancelled out and the analysis becomes more efficient. However, such a solution is not general, as it is not feasible, e.g., when we have unbalanced designs and heteroscedastic data. With the appropriate approach, sound analyses can also be made in two-steps (Damesa et al., 2017). From my point of view, it is reasonable to search for more general solutions to deal with one-step analyses.
Based on our experience with traditional ANOVA models, we might think of taking the block effect as fixed and fit it as and additive term. See the code below.
mod.reg <- lm(yield ~ block + density, data=dataset)
summary(mod.reg)
##
## Call:
## lm(formula = yield ~ block + density, data = dataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.6062 -0.8242 -0.3315 0.7505 4.6244
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 29.10462 0.57750 50.397 < 2e-16 ***
## block2 4.57750 0.74668 6.130 4.81e-08 ***
## block3 7.05875 0.74668 9.453 4.49e-14 ***
## block4 -3.98000 0.74668 -5.330 1.17e-06 ***
## block5 6.17625 0.74668 8.272 6.37e-12 ***
## block6 5.92750 0.74668 7.938 2.59e-11 ***
## block7 1.23750 0.74668 1.657 0.10199
## block8 1.25500 0.74668 1.681 0.09733 .
## block9 2.34875 0.74668 3.146 0.00245 **
## block10 2.25125 0.74668 3.015 0.00359 **
## density -0.26744 0.00701 -38.149 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.493 on 69 degrees of freedom
## Multiple R-squared: 0.9635, Adjusted R-squared: 0.9582
## F-statistic: 181.9 on 10 and 69 DF, p-value: < 2.2e-16With regression, this solution is not convincing. Indeed, the above model assumes that the blocks produce an effect only on the intercept of the regression line, while the slope is unaffected. Is this a reasonable assumption? I vote no.
Let’s check this by fitting a different regression model per block (ten different slopes + ten different intercepts):
mod.reg2 <- lm(yield ~ block/density + block, data=dataset)
anova(mod.reg, mod.reg2)
## Analysis of Variance Table
##
## Model 1: yield ~ block + density
## Model 2: yield ~ block/density + block
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 69 153.88
## 2 60 115.75 9 38.135 2.1965 0.03465 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The p-level confirms that the block had a significant effect both on the intercept and on the slope. To describe such an effect we need 20 parameters in the model, which is not very parsimonious. And above all: which regression line do we use for predictions? Taking the block effect as fixed is clearly sub-optimal with regression models.
The question is: can we fit a simpler and clearer model? The answer is: yes. Why don’t we take the block effect as random? This is perfectly reasonable. Let’s do it.
modMix.1 <- lme(yield ~ density, random = ~ density|block, data=dataset)
summary(modMix.1)
## Linear mixed-effects model fit by REML
## Data: dataset
## AIC BIC logLik
## 340.9166 355.0569 -164.4583
##
## Random effects:
## Formula: ~density | block
## Structure: General positive-definite, Log-Cholesky parametrization
## StdDev Corr
## (Intercept) 3.16871858 (Intr)
## density 0.02255249 0.09
## Residual 1.38891957
##
## Fixed effects: yield ~ density
## Value Std.Error DF t-value p-value
## (Intercept) 31.78987 1.0370844 69 30.65311 0
## density -0.26744 0.0096629 69 -27.67704 0
## Correlation:
## (Intr)
## density -0.078
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.9923722 -0.5657555 -0.1997103 0.4961675 2.6699060
##
## Number of Observations: 80
## Number of Groups: 10The above fit shows that the random effects (slope and intercept) are sligthly correlated (r = 0.091). We might like to try a simpler model, where random effects are independent. To do so, we need to consider that the above model is equivalent to the following model:
modMix.1 <- lme(yield ~ density, random = list(block = pdSymm(~density)), data=dataset)It’s just two different ways to code the very same model. However, this latter coding, based on a ‘pdMat’ structure, can be easily modified to remove the correlation. Indeed, ‘pdSymm’ specifies a totally unstructured variance-covariance matrix for random effects and it can be replaced by ‘pdDiag’, which specifies a diagonal matrix, where covariances (off-diagonal terms) are constrained to 0. The coding is as follows:
modMix.2 <- lme(yield ~ density, random = list(block = pdDiag(~density)), data=dataset)
summary(modMix.2)
## Linear mixed-effects model fit by REML
## Data: dataset
## AIC BIC logLik
## 338.952 350.7355 -164.476
##
## Random effects:
## Formula: ~density | block
## Structure: Diagonal
## (Intercept) density Residual
## StdDev: 3.198263 0.02293222 1.387148
##
## Fixed effects: yield ~ density
## Value Std.Error DF t-value p-value
## (Intercept) 31.78987 1.0460272 69 30.39105 0
## density -0.26744 0.0097463 69 -27.44019 0
## Correlation:
## (Intr)
## density -0.139
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -1.9991173 -0.5451478 -0.1970267 0.4925090 2.6700386
##
## Number of Observations: 80
## Number of Groups: 10
r
anova(modMix.1, modMix.2)
## Model df AIC BIC logLik Test L.Ratio p-value
## modMix.1 1 6 340.9166 355.0569 -164.4583
## modMix.2 2 5 338.9520 350.7355 -164.4760 1 vs 2 0.03535079 0.8509The model could be further simplified. For example, the code below shows how we could fit models with either random intercept or random slope.
#Model with only random intercept
modMix.3 <- lme(yield ~ density, random = list(block = ~1), data=dataset)
#Alternative
#random = ~ 1|block
#Model with only random slope
modMix.4 <- lme(yield ~ density, random = list(block = ~ density - 1), data=dataset)
#Alternative
#random = ~density - 1 | blockAn example with nonlinear regression
The problem may become trickier if we have a nonlinear relationship. Let’s have a look at another similar dataset (‘YieldLossB.csv’), that is also available on gitHub. It represents another experiment where sunflower was grown with the same increasing densities of another weed (0, 14, 19, 28, 32, 38, 54, 82 plants per \(m^2\)), on a randomised complete block design, with 8 blocks. In this case, the yield loss was recorded and analysed.
rm(list=ls())
dataset <- read.csv("https://raw.githubusercontent.com/OnofriAndreaPG/agroBioData/master/YieldLossB.csv",
header=T)
dataset$block <- factor(dataset$block)
head(dataset)
## block density yieldLoss
## 1 1 0 1.532
## 2 2 0 -0.661
## 3 3 0 -0.986
## 4 4 0 -0.697
## 5 5 0 -2.264
## 6 6 0 -1.623
r
plot(yieldLoss ~ density, data = dataset)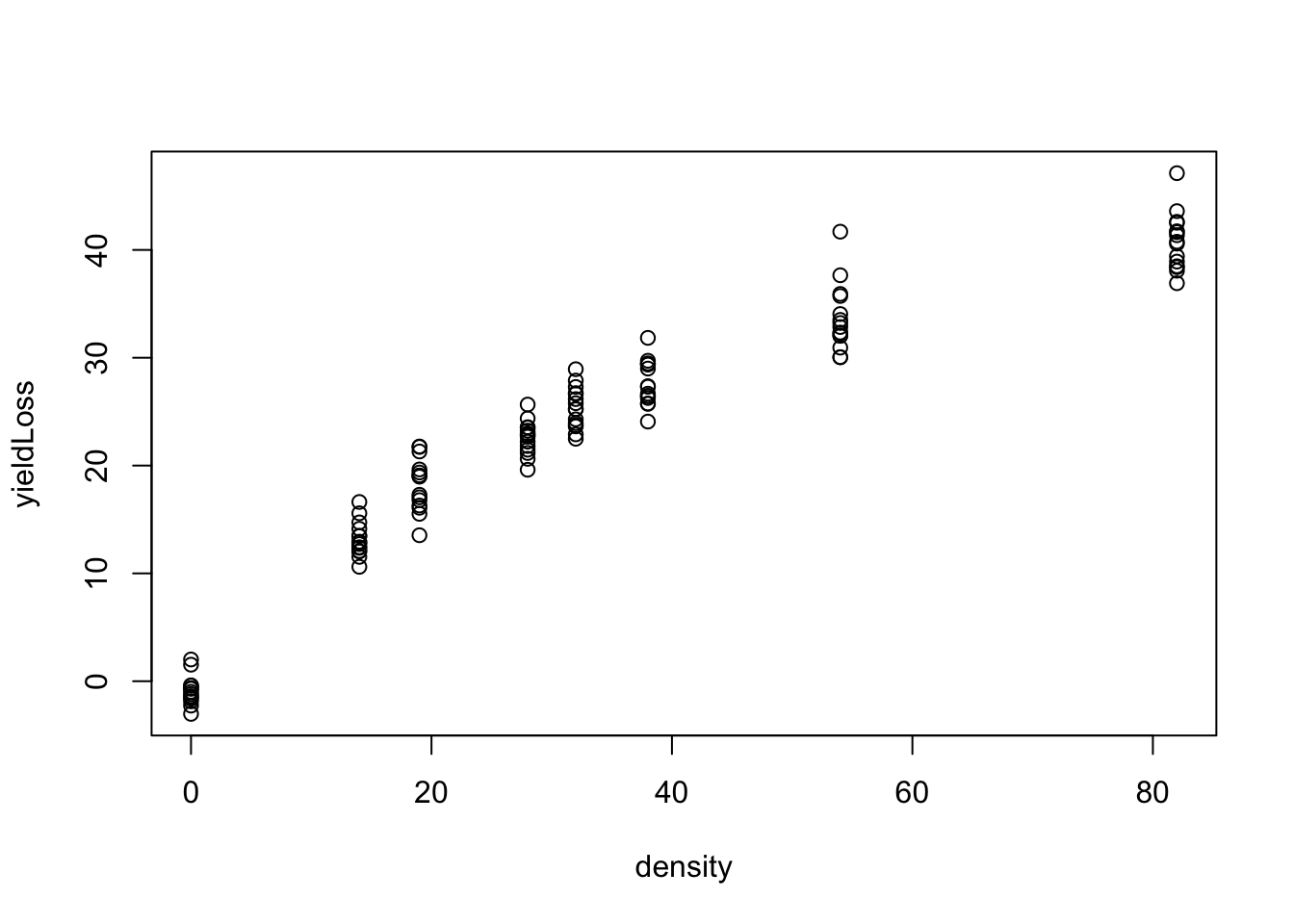
A swift plot shows that the relationship between density and yield loss is not linear. Literature references (Cousens, 1985) show that this could be modelled by using a rectangular hyperbola:
\[YL = \frac{i \, D}{1 + \frac{i \, D}{a}}\]
where \(YL\) is the yield loss, \(D\) is weed density, \(i\) is the slope at the origin of axes and \(a\) is the maximum asymptotic yield loss. This function, together with self-starters, is available in the ‘NLS.YL()’ function in the ‘aomisc’ package, which is the accompanying package for this blog. If you do not have this package, please refer to this link to download it.
The problem is the very same as above: the block effect may produce random fluctuations for both model parameters. The only difference is that we need to use the ‘nlme()’ function instead of ‘lme()’. With nonlinear mixed models, I strongly suggest you use a ‘groupedData’ object, which permits to avoid several problems. The second line below shows how to turn a data frame into a ‘groupedData’ object.
library(aomisc)
datasetG <- groupedData(yieldLoss ~ 1|block, dataset)
nlin.mix <- nlme(yieldLoss ~ NLS.YL(density, i, A), data=datasetG,
fixed = list(i ~ 1, A ~ 1),
random = i + A ~ 1|block)
summary(nlin.mix)
## Nonlinear mixed-effects model fit by maximum likelihood
## Model: yieldLoss ~ NLS.YL(density, i, A)
## Data: datasetG
## AIC BIC logLik
## 474.8228 491.5478 -231.4114
##
## Random effects:
## Formula: list(i ~ 1, A ~ 1)
## Level: block
## Structure: General positive-definite, Log-Cholesky parametrization
## StdDev Corr
## i 0.1112841 i
## A 4.0444816 0.195
## Residual 1.4142267
##
## Fixed effects: list(i ~ 1, A ~ 1)
## Value Std.Error DF t-value p-value
## i 1.23238 0.0382246 104 32.24035 0
## A 68.52305 1.9449780 104 35.23076 0
## Correlation:
## i
## A -0.408
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -2.4416777 -0.7049390 -0.1805691 0.3385459 2.8788990
##
## Number of Observations: 120
## Number of Groups: 15Similarly to linear mixed models, the above coding implies correlated random effects (r = 0.194). Alternatively, the above model can be coded by using a ’pdMat construct, as follows:
nlin.mix2 <- nlme(yieldLoss ~ NLS.YL(density, i, A), data=datasetG,
fixed = list(i ~ 1, A ~ 1),
random = pdSymm(list(i ~ 1, A ~ 1)))
summary(nlin.mix2)
## Nonlinear mixed-effects model fit by maximum likelihood
## Model: yieldLoss ~ NLS.YL(density, i, A)
## Data: datasetG
## AIC BIC logLik
## 474.8225 491.5474 -231.4112
##
## Random effects:
## Formula: list(i ~ 1, A ~ 1)
## Level: block
## Structure: General positive-definite
## StdDev Corr
## i 0.1112837 i
## A 4.0468443 0.194
## Residual 1.4141993
##
## Fixed effects: list(i ~ 1, A ~ 1)
## Value Std.Error DF t-value p-value
## i 1.23242 0.038225 104 32.24114 0
## A 68.52050 1.945186 104 35.22568 0
## Correlation:
## i
## A -0.409
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -2.4413852 -0.7049358 -0.1805300 0.3385252 2.8787256
##
## Number of Observations: 120
## Number of Groups: 15Now we can try to simplify the model, for example by excluding the correlation between random effects.
nlin.mix3 <- nlme(yieldLoss ~ NLS.YL(density, i, A), data=datasetG,
fixed = list(i ~ 1, A ~ 1),
random = pdDiag(list(i ~ 1, A ~ 1)))
summary(nlin.mix3)
## Nonlinear mixed-effects model fit by maximum likelihood
## Model: yieldLoss ~ NLS.YL(density, i, A)
## Data: datasetG
## AIC BIC logLik
## 472.9076 486.8451 -231.4538
##
## Random effects:
## Formula: list(i ~ 1, A ~ 1)
## Level: block
## Structure: Diagonal
## i A Residual
## StdDev: 0.1172791 4.389173 1.408963
##
## Fixed effects: list(i ~ 1, A ~ 1)
## Value Std.Error DF t-value p-value
## i 1.23243 0.0393514 104 31.31852 0
## A 68.57655 1.9905549 104 34.45097 0
## Correlation:
## i
## A -0.459
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -2.3577292 -0.6849962 -0.1785860 0.3255925 2.8592764
##
## Number of Observations: 120
## Number of Groups: 15With a little fantasy, we can easily code several alternative models to represent alternative hypotheses about the observed data. Obviously, the very same method can be used (and SHOULD be used) to account for other grouping factors, such as main-plots in split-plot designs or plots in repeated measure designs.
Happy coding!
Andrea Onofri
Department of Agricultural, Food and Environmental Sciences
University of Perugia (Italy)
Borgo XX Giugno 74
I-06121 - PERUGIA
References
- Cousens, R., 1985. A simple model relating yield loss to weed density. Annals of Applied Biology 107, 239–252. https://doi.org/10.1111/j.1744-7348.1985.tb01567.x
- Jensen, S.M., Schaarschmidt, F., Onofri, A., Ritz, C., 2018. Experimental design matters for statistical analysis: how to handle blocking: Experimental design matters for statistical analysis. Pest Management Science 74, 523–534. https://doi.org/10.1002/ps.4773
- Onofri, A., Carbonell, E.A., Piepho, H.-P., Mortimer, A.M., Cousens, R.D., 2010. Current statistical issues in Weed Research. Weed Research 50, 5–24.