Chapter 10 Multi-way ANOVA models
Statisticians, like artists, have the bad habit of falling in love with their models (G. Box)
In Chapter 7 we showed how we can fit linear models with one categorical predictor and one response variable (one-way ANOVA models). With those models, apart from differences due to the experimental treatments, all units must be completely independent and there should not be any other systematic sources of variability. On the contrary, with the most common experiments laid down as Randomised Complete Blocks (RCBDs) or, less commonly, as Latin Square (LSD), apart from the treatment factor, we also have, respectively, one and two blocking factors, which represent additional sources of systematic variability. Indeed, the block effect produces a more or less relevant increase/decrease in the observed response, with respect to the overall mean; for example, in a field experiment with two blocks, the most fertile one might might produce a yield increase of 1 t/ha, while the other one will produce a corresponding yield decrease of the same amount. Such yield variations will be systematically shared by all plots located in the same block.
In principle, we should not fit one-way ANOVA models to the data obtained from RCBDs or LSDs; if we do so, the residuals will also contain the block effect (\(\pm\) 1 t/ha, in the previous example) and, therefore, those obtained in the same block will be more alike than the residuals obtained in different blocks. Consequently, the basic assumption of independence will no longer be valid; in order to avoid this, we need a new type of models that can account for treatment effects and block effects at the same time.
10.1 Motivating example: a genotype experiment in blocks
Let’s consider a field experiment to compare eight winter wheat genotypes, laid down in complete blocks, with three replicates. Each block consists of eight plots, to which genotypes were randomly allocated, one replicate per block; the blocks are laid out one beside the other, following the direction of the fertility gradient, so that plots within each block were as homogeneous as possible. The response variable is the yield, in tons per hectare.
The dataset is available as the ‘csv’ file ‘WinterWheat2002.csv’, which can be loaded from an external repository, as shown in the box below.
repo <- "https://www.casaonofri.it/_datasets/"
file <- "WinterWheat2002.csv"
pathData <- paste(repo, file, sep = "")
dataset <- read.csv(pathData, header = T)
head(dataset)
## Plot Block Genotype Yield
## 1 57 A COLOSSEO 4.31
## 2 61 B COLOSSEO 4.73
## 3 11 C COLOSSEO 5.64
## 4 60 A CRESO 3.99
## 5 10 B CRESO 4.82
## 6 42 C CRESO 4.17The description of the dataset for each genotype (mean and standard deviation) is left to the reader, as an exercise.
10.2 Model definition
Considering the experimental design, the yield of each plot depends on:
- the genotype;
- the block;
- other random and unknown effects.
Consequently, a linear model can be specified as:
\[ Y_{ij} = \mu + \gamma_i + \alpha_j + \varepsilon_{ij}\]
where \(Y_{ij}\) is the yield for the plot in the \(i\)th block and with the \(j\)th genotype, \(\mu\) is the intercept, \(\gamma_i\) is the effect of the \(i\)th block, \(\alpha_j\) is the effect of the \(j\)th genotype and \(\varepsilon\) is the residual plot error, which is assumed as gaussian, with mean equal to 0 and standard deviation equal to \(\sigma\). With respect to the one-way ANOVA model, we have the additional block effect, which accounts for the grouping of observations, so that the residuals only ‘contain’ random and independent effects.
As we did for the one-way ANOVA model, we need to put constraints on \(\alpha\) and \(\gamma\) values, so that model parameters are estimable. Regardless of the constraint, we have 7 genotype parameters and 2 block parameters to estimate, apart from \(\sigma\).
10.3 Model fitting by hand
Normally, the estimation process is done with R, by using the least squares method. For the sake of exercise, we do the calculations by hand, using the method of moments, which is correct whenever the experiment is balanced (same number of replicates for all genotypes). Hand-calculations are similar to those proposed in Chapter 7 and, if you had enough with them, you can safely skip this section and jump to the next one.
For hand-calculations, we prefer to use the sum-to-zero contraint; therefore, \(\mu\) is the overall mean, \(\alpha_1\) to \(\alpha_8\) are the effects of the genotypes, as differences with respect to the overall mean, \(\gamma_1\) to \(\gamma_3\) are the effects of blocks. Owing to the sum-to-zero constraint, \(\alpha_8\) and \(\gamma_3\) must obey the following restrictions: \(\alpha_8 = -\sum_{i=1}^{7} \alpha_i\) and \(\gamma_3 = -\sum_{i=1}^{2} \gamma_i\).
The initial step is to calculate the overall mean and the means for genotypes and blocks. As usual, we use the tapply() function to accomplish this task.
allMean <- mean(dataset$Yield)
gMeans <- tapply(dataset$Yield, dataset$Genotype, mean)
bMeans <- tapply(dataset$Yield, dataset$Block, mean)
allMean
## [1] 4.424583
gMeans
## COLOSSEO CRESO DUILIO GRAZIA IRIDE SANCARLO SIMETO
## 4.893333 4.326667 4.240000 4.340000 4.963333 4.503333 3.340000
## SOLEX
## 4.790000
bMeans
## A B C
## 4.20625 4.41500 4.65250Now we can calculate yield differences between the genotype means and the overall mean, so that we obtain the genotype effects \(\alpha_i\). We do the same to obtain the block effects, as shown in the box below.
alpha <- gMeans - allMean
alpha
## COLOSSEO CRESO DUILIO GRAZIA IRIDE
## 0.46875000 -0.09791667 -0.18458333 -0.08458333 0.53875000
## SANCARLO SIMETO SOLEX
## 0.07875000 -1.08458333 0.36541667
gamma <- bMeans - allMean
gamma
## A B C
## -0.218333333 -0.009583333 0.227916667It is useful to sort the dataset by genotypes and blocks and visualise all model parameters in a table; to do so, we need to repeat each genotype effects three times (the number of blocks) and the whole vector of block effects for eight times (the number of genotypes). Lately, we add to the table the expected values (\(Y_{E(ij)} = \mu + \gamma_i + \alpha_j\)) and the residuals (\(\varepsilon_ij = Y_{ij} - Y_{E(ij)}\)). The resulting data frame is shown in the box below.
alpha <- rep(alpha, each = 3)
gamma <- rep(gamma, 8)
mu <- allMean
YE <- mu + gamma + alpha
epsilon <- dataset$Yield - YE
lmod <- data.frame(dataset, mu, gamma, alpha,
YE, epsilon)
print(lmod, digits = 4)
## Plot Block Genotype Yield mu gamma alpha YE epsilon
## 1 57 A COLOSSEO 4.31 4.425 -0.218333 0.46875 4.675 -0.36500
## 2 61 B COLOSSEO 4.73 4.425 -0.009583 0.46875 4.884 -0.15375
## 3 11 C COLOSSEO 5.64 4.425 0.227917 0.46875 5.121 0.51875
## 4 60 A CRESO 3.99 4.425 -0.218333 -0.09792 4.108 -0.11833
## 5 10 B CRESO 4.82 4.425 -0.009583 -0.09792 4.317 0.50292
## 6 42 C CRESO 4.17 4.425 0.227917 -0.09792 4.555 -0.38458
## 7 29 A DUILIO 4.24 4.425 -0.218333 -0.18458 4.022 0.21833
## 8 48 B DUILIO 4.10 4.425 -0.009583 -0.18458 4.230 -0.13042
## 9 81 C DUILIO 4.38 4.425 0.227917 -0.18458 4.468 -0.08792
## 10 32 A GRAZIA 4.07 4.425 -0.218333 -0.08458 4.122 -0.05167
## 11 65 B GRAZIA 4.18 4.425 -0.009583 -0.08458 4.330 -0.15042
## 12 28 C GRAZIA 4.77 4.425 0.227917 -0.08458 4.568 0.20208
## 13 19 A IRIDE 5.18 4.425 -0.218333 0.53875 4.745 0.43500
## 14 79 B IRIDE 4.88 4.425 -0.009583 0.53875 4.954 -0.07375
## 15 55 C IRIDE 4.83 4.425 0.227917 0.53875 5.191 -0.36125
## 16 5 A SANCARLO 4.34 4.425 -0.218333 0.07875 4.285 0.05500
## 17 37 B SANCARLO 4.41 4.425 -0.009583 0.07875 4.494 -0.08375
## 18 70 C SANCARLO 4.76 4.425 0.227917 0.07875 4.731 0.02875
## 19 2 A SIMETO 3.03 4.425 -0.218333 -1.08458 3.122 -0.09167
## 20 34 B SIMETO 3.21 4.425 -0.009583 -1.08458 3.330 -0.12042
## 21 67 C SIMETO 3.78 4.425 0.227917 -1.08458 3.568 0.21208
## 22 74 A SOLEX 4.49 4.425 -0.218333 0.36542 4.572 -0.08167
## 23 9 B SOLEX 4.99 4.425 -0.009583 0.36542 4.780 0.20958
## 24 56 C SOLEX 4.89 4.425 0.227917 0.36542 5.018 -0.12792From the above data frame, we can calculate all sum of squares; in detail, the residual sum of squares is obtained by squaring and summing up the residuals:
Likewise, the sum of squares for blocks and genotypes is obtained by squaring and summing up the \(\gamma\) and \(\alpha\) effects.
If we calculate the total deviance for all observations, we can confirm that this was partitioned in three parts: the first one is due to the block effects, the second one is due to the genotype effects and the third one is due to all other unknown sources of variability.
The above hand-calculations should suffice for those who would like to see what happens ‘under the hood’. Now, we can go back to model fitting with R.
10.4 Model fitting with R
As shown in Chapter 7, ANOVA models with more than one predictor can be fit by using the lm() function and adding the block term along with the treatment term. It is fundamental that the block variable is transformed into a factor variable, otherwise R would consider it as numeric and would fit a regression model, instead of an ANOVA model (see later in this book). This error is very common in the most frequent case where a numeric variable is used to represent the blocks and it is easily spotted by checking the number of degrees of freedom in the final ANOVA table; indeed, if this number does not appear to correspond to our expectations (that is the number of blocks minus one; see below), it may mean that our model definition was wrong.
In the box below, we also transform the genotype variable into a factor, although this is optional, as the genotypes are represented by a character vector and not by a numeric vector.
dataset$Block <- factor(dataset$Block)
dataset$Genotype <- factor(dataset$Genotype)
mod <- lm(Yield ~ Block + Genotype, data = dataset)We do not inspect model coefficients, as they are not particularly useful in this instance. However, should you like to do so, you can use the summary() method; please, remember that the treatment constraint is used by default in R.
10.4.1 Model checking
As we have discussed in Chapter 8, once we have got the residuals we should inspect them, searching for possible deviations from basic assumptions. Therefore, we produce a plot of residuals against expected values and a QQ-plot, by using the code below. The output is shown in Figure 10.1.
par(mfrow=c(1,2))
plot(mod, which = 1)
plot(mod, which = 2)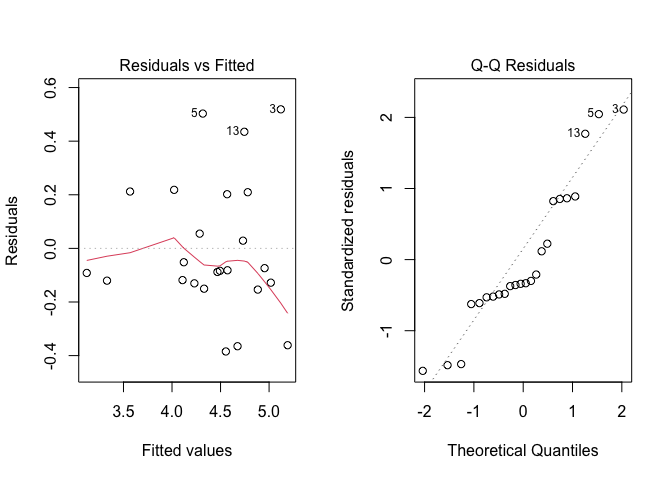
Figure 10.1: Graphical analyses of residuals for the genotype experiment
From that Figure, we observe that there are some slight signs of heteroscedasticity (see plot on the left side), although the Levene’s test is not significant (but it is on the borderline of significance; see the box below). We decide not to address this problem, for the sake of simplicity and based on the unsignificant Levene’s test.
epsilon <- residuals(mod)
anova(lm(abs(epsilon) ~ factor(Genotype), data = dataset))
## Analysis of Variance Table
##
## Response: abs(epsilon)
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(Genotype) 7 0.24819 0.035455 2.2162 0.08887 .
## Residuals 16 0.25597 0.015998
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 110.4.2 Variance partitioning
Variance partitioning with R is performed by applying the anova() method to the ‘lm’ object.
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Block 2 0.7977 0.39883 3.8502 0.0465178 *
## Genotype 7 5.6305 0.80436 7.7651 0.0006252 ***
## Residuals 14 1.4502 0.10359
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The sum of squares are the same as those obtained by hand-calculations and they measure the amount of data variability that can be attributed to the different effects. Sum of squares cannot be directly compared, because they are based on different degrees of freedom and, therefore, we calculate the corresponding variances.
The number of Degrees of Freedom (DF) for the block effect is equal to the number of blocks \(b\) minus one (\(DF_b = b - 1 = 2\)), while the number of DF for the genotype effect is equal to the number of genotypes \(g\) minus one (\(DF_g = g - 1 = 7\)). The number of DF for the residual sum of squares is \(g \times (b - 1)\) as in Chapter 7 (the number of blocks is equal to the number of replicates is the number of replicates), but we have to subtract \(DF_b\), so that we have \(DF_r = g \times (b - 1) - (b - 1) = (g - 1) \times (b - 1) = 14\).
The residual mean square is \(1.450208/14 = 0.10359\) and, from there, we can get an estimate of \(\sigma = \sqrt{0.10359} = 0.3218483\). More easily, we can get \(\sigma\) by using the summary() method and the ‘$sigma’ extractor.
Subsequently, we start our inference process by using \(\sigma\) to estimate the standard error for a mean (SEM) and the standard error for a difference (SED), which are, respectively, equal to \(0.3218483/\sqrt{3} = 0.186\) and \(\sqrt{2} \times 0.3218483/\sqrt{3} = 0.263\).
Next, we set our null hypotheses as:
\[H_0: \gamma_1 = \gamma_2 = \gamma_3 = \gamma\]
and:
\[H_0: \alpha_1 = \alpha_2 = ... = \alpha_8 = 0\]
Indeed, for a RCBD, we have two F ratios, with the same denominator (residual mean square) and, respectively, the mean square for blocks and the mean square for genotypes as numerators. Based on those F-ratios, we see that both the nulls can be rejected, as the corresponding P-values are below the 0.05 yardstick. In particular, we are interested about the genotype effect, as we introduced the blocks only to be able to account for possible plot-to-plot fertility differences. Consequently, we only proceed to pairwise comparisons between the genotypes.
Please, note that we have 8 genotypes, implying that we need to test \(8 \time 7 / 2 = 27\) pairwise differences, which is enough to justify the adoption of a multiplicity correction. For the sake of clarity, we report the means and adopt a letter display, where we order the means in decreasing yield order (the best is the one with highest yield), by using the argument ‘reverse = T’.
library(emmeans)
medie <- emmeans(mod, ~factor(Genotype))
multcomp::cld(medie, Letters = LETTERS, reverse = T)
## Genotype emmean SE df lower.CL upper.CL .group
## IRIDE 4.96 0.186 14 4.56 5.36 A
## COLOSSEO 4.89 0.186 14 4.49 5.29 A
## SOLEX 4.79 0.186 14 4.39 5.19 A
## SANCARLO 4.50 0.186 14 4.10 4.90 A
## GRAZIA 4.34 0.186 14 3.94 4.74 A
## CRESO 4.33 0.186 14 3.93 4.73 A
## DUILIO 4.24 0.186 14 3.84 4.64 AB
## SIMETO 3.34 0.186 14 2.94 3.74 B
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 8 estimates
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.The comment of results is left as an exercise.
10.5 Another example: comparing working protocols
In Chapter 2, we introduced an example relating to the evaluation of the time required to accomplish a certain task, by using four different protocols. Four technicians were involved and each one worked with the four methods in different randomised shifts. The protocols were allocated to the different shifts and technicians so that we could have one replicate for each technician and shift. In the end, the dataset consists of one experimental factor (the protocol, with four levels) and two blocking factors (the technician and the shift for each technician). The results are available in the usual online repository.
filePath <- "https://www.casaonofri.it/_datasets/"
fileName <- "Technicians.csv"
file <- paste(filePath, fileName, sep = "")
dataset <- read.csv(file, header=T)
head(dataset)
## Shift Technician Method Time
## 1 I Andrew C 90
## 2 II Andrew B 90
## 3 III Andrew A 89
## 4 IV Andrew D 104
## 5 I Anna D 96
## 6 II Anna C 91The time required for the task can be described as follows:
\[Y_{ijk} = \mu + \gamma_k + \beta_j + \alpha_i + \varepsilon_{ijk}\]
where \(\mu\) is the intercept, \(\gamma\) is the effect of the \(k\)th shift, \(\beta\) is the effect of the \(j\)th technician and \(\alpha\) is the effect of the \(i\)th protocol. The elements \(\varepsilon_{ijk}\) represent the individual random sources of experimental error; they are assumed as gaussian, with mean equal to 0 and standard deviation equal to \(\sigma\).
For this example, model fitting is performed only with R, by including all blocking effects in the model.
From the model fit object we extract the residuals and check for the basic assumptions for linear models, by using the usual plot() function. The resulting plots are shown in Figure 10.2.
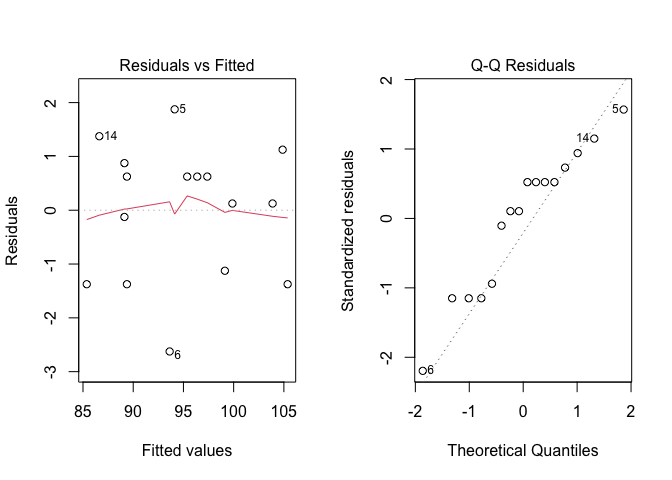
Figure 10.2: Graphical analyses of residuals for a latin square experiment
We do not see problems of any kind and, therefore, we proceed to variance partitioning, to test the significance of all experimental factors.
anova(mod)
## Analysis of Variance Table
##
## Response: Time
## Df Sum Sq Mean Sq F value Pr(>F)
## Method 3 145.69 48.563 12.7377 0.0051808 **
## Technician 3 17.19 5.729 1.5027 0.3065491
## Shift 3 467.19 155.729 40.8470 0.0002185 ***
## Residuals 6 22.87 3.812
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The difference between protocols is significant, as well as the difference between shifts, while the technicians did not differ significantly. We might be interested in selecting the best working protocols, which can be done by using pairwise comparisons. I will leave this part to you, as an exercise.