Capitolo 5 Esperimenti, stime ed incertezza

Abbiamo già visto che un esperimento scientifico non è altro che un’operazione di campionamento, con la quale io, invece che studiare una popolazione enorme di soggetti, posso studiarne un gruppo sufficientemente piccolo e compatibile con le mie limitate risorse di tempo e denaro. Anche se il campione estratto è effettivamente rappresentativo della popolazione, rimane il fatto che esso è il risultato di uno solo degli infiniti sforzi di campionamento possibili. Con due importanti conseguenze:

le sue caratteristiche non necessariamente riflettono quelle della popolazione che lo ha generato;
campionamenti successivi forniscono risultati diversi, perché diversi sono i soggetti e, spesso, anche le condizioni in cui l’esperimento viene eseguito.

Di conseguenza, al di là del campione, il nostro interesse rimane fondamentalmente rivolto verso la popolazione che lo ha generato. Ci dobbiamo chiedere quale sia la relazione tra le caratteristiche del campione e quelle della popolazione da cui esso è estratto. Questo processo logico prende il nome di inferenza statistica e può essere condotto secondo le teorie di Karl Pearson (1857-1936), Egon Pearson (suo figlio: 1895-1980) e Jarzy Neyman (1894-1981), oltre al solito Ronald Fisher.

5.1 L’analisi dei dati: gli ‘ingredienti’ fondamentali

Richiamiamo il percorso logico che abbiamo introdotto nel capitolo precedente:

I fenomeni biologici seguono una legge di natura (verità ‘vera’), che ne costituisce il meccanismo deterministico fondamentale.
Quando si organizza un esperimento, i soggetti sperimentali obbediscono a questo meccanismo di fondo, al quale tuttavia si sovrappongono molto altri elementi di ‘confusione’, altamente incontrollabili, che vanno sotto il nome di errore sperimentale.
L’osservazione sperimentale è quindi un’immagine confusa della verità vera e, soprattutto, l’osservazione sperimentale tende ad essere diversa per ogni sforzo di campionamento.
Compito del ricercatore è quello di separare l’informazione (che rappresenta la verità ‘vera’) dal ‘rumore di fondo’ provocato dall’errore sperimentale.

Questo dualismo tra verità ‘vera’ (inconoscibile) e verità sperimentale (esplorabile tramite un esperimento opportunamente pianificato) è l’aspetto centrale di tutta la biometria ed è schematizzato nella figura 5.1. Di esso abbiamo fatto menzione più volte nei capitoli precedenti.

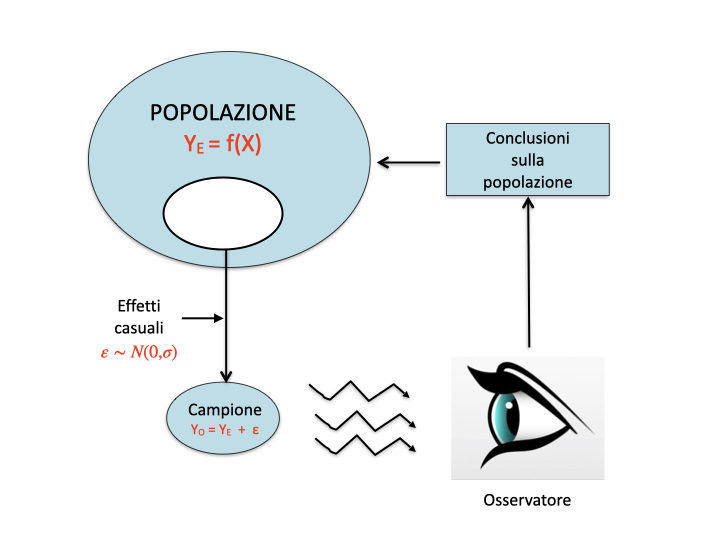
Figure 5.1: Osservazioni sperimentali e meccanismi perturbativi

In questo percorso logico ci sono due aspetti fondamentali che debbono essere attentamente valutati:

modello di generazione dei dati sperimentali;
sampling distribution (o sample space).

Chiariamo i due concetti con un esempio.

5.2 Esempio: una soluzione erbicida

Immaginiamo questa situazione: abbiamo una soluzione erbicida a concentrazione pari a 120 \(mg/l\), che viene misurata tramite un gascromatografo. Lo strumento di misura, unitamente a tutte le altre fonti ignote di errore, produce un coefficiente di variabilità del 10% (corrispondete ad una deviazione standard pari a 12 \(mg/l\)). Facciamo le analisi in triplicato, come usuale per questo tipo di lavori.

5.2.1 Il modello dei dati

In primo luogo, ci chiediamo quale sia il modello matematico che genera le nostre osservazioni. Considerando quanto detto nel capitolo precedente, possiamo assumere che:

\[ Y_i = \mu + \varepsilon_i\]

dove:

\[ \varepsilon_i \sim N(\mu, \sigma)\]

cioè possiamo assumere che i risultati delle nostre misure siano normalmente distribuiti con media \(\mu = 120\) e deviazione standard \(\sigma = 12\).

Con queste informazioni possiamo simulare un esperimento con R, ottenendo i seguenti risultati:

set.seed(1234)
Y <- rnorm(3, 120, 12)
Y
## [1] 125.1584 114.7349 105.6998

5.2.2 Analisi dei dati: stima dei parametri

Nelle due equazioni sovrastanti, gli elementi incogniti sono \(\mu\) e \(\sigma\). In realtà, dato che si tratta di una simulazione, sappiamo che essi sono pari, rispettivamente, a 120 e 12; tuttavia, nella realtà questa informazione sarebbe totalmente sconosciuta. Guardando il campione, le nostre migliori stime \(\mu\) e \(\sigma\), che chiameremo rispettivamente \(m\) ed \(s\), sono pari rispettivamente alla media e alla deviazione standard del campione.

m <- mean(Y)
s <- sd(Y)
m; s
## [1] 115.1977
## [1] 9.737554

Questo processo con il quale assegniamo alla popolazione le caratteristiche del campione prende il nome di stima puntuale dei parametri. Vediamo ancora una volta che l’osservazione sperimentale non coincide con la verità ‘vera’ (\(m \ne \mu\) e \(s \ne \sigma)\), ma non siamo molto distanti, considerando il 10% di variabilità dello strumento di analisi. Tuttavia, visto che dobbiamo trarre conclusioni che riguardano la popolazione e non il campione, è giustificato da parte nostra un atteggiamento prudenziale: prima di dire che la concentrazione erbicida nella soluzione è pari 115.1976637, dobbiamo chiederci: che cosa succederebbe se ripetessimo l’esperimento molte altre volte?

5.2.3 La ‘sampling distribution’

In questo caso l’esperimento è solo ‘elettronico’ e possiamo quindi ripeterlo un numero anche molto elevato di volte, seguendo questa procedura:

Ripetiamo l’estrazione precedente per 100’000 volte (ripetiamo l’analisi chimica per 100’000 volte, sempre con tre repliche)
Otteniamo 100’000 medie
Calcoliamo la media delle medie e la deviazione standard delle medie

# Simulazione MONTE CARLO - Esempio 1
set.seed(1234)
result <- rep(0, 100000)
for (i in 1:100000){
  sample <- rnorm(3, 120, 12)
  result[i] <- mean(sample)
}
mean(result)
## [1] 119.9882
sd(result)
## [1] 6.924185

In sostanza, la simulazione Monte Carlo ci consente di fare quello che dovremmo sempre fare, cioè ripetere l’esperimento un numero di volte molto elevato, anche se finito (un numero infinito è chiaramente impossibile!). A questo punto abbiamo in mano una popolazione di medie, che viene detta sampling distribution, un ‘oggetto’ abbastanza ‘teorico’, ma fondamentale per la statistica frequentista, perché caratterizza la variabilità dei risultati di un esperimento, e quindi la sua riproducibilità.

Notiamo che:

La media delle medie è praticamente coincidente con \(\mu\), la verità ‘vera’. Ciò conferma che l’unico modo di ottenere risultati totalmente precisi è ripetere infinite volte l’esperimento;
La deviazione standard delle medie è pari a 6.9241851. Questo valore prende il nome di errore standard della media (SEM).

Esploriamo meglio la sampling distribution. Con R possiamo provare a discretizzarla e a riportarla su di un grafico a barre (figura 5.2 ).

b <- seq(80, 160, by=2.5)
hist(result, breaks = b, freq=F, xlab = expression(paste(m)),
  ylab="Density", main="")
curve(dnorm(x, 120, 6.94), add = TRUE, col = "red")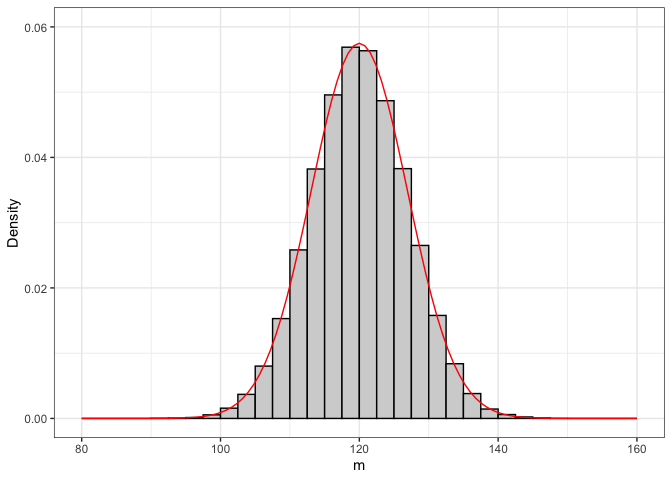

Figure 5.2: Sampling distribution empirica e teorica

5.2.4 L’errore standard

La sampling distribution che abbiamo ottenuto con la simulazione Monte Carlo è puramente empirica. Sarebbe interessante capire con più esattezza se esiste una funzione di densità che permetta di descriverla con esattezza. In effetti, il grafico precedente mostra che la sampling distribution assomiglia molto ad una distribuzione normale, con media pari a 120 e deviazione standard pari all’errore standard.

Formalmente, il problema si può risolvere grazie alla legge di propagazione degli errori, che stabilisce tre importanti elementi:

Se ho due variabili normalmente distribuite e le sommo tra di loro, la variabile risultante è ancora normale. Se ho una variabile normalmente distribuita e la moltiplico per una costante, la variabile risultante è ancora normale.
Per variabili indipendenti, la varianza della somma è uguale alla somma delle varianze.
La varianza del prodotto di una variabile per una costante \(k\) è pari alla varianza della variabile originale moltiplicata per \(k^2\).

Consideriamo che, quando preleviamo alcuni individui da una popolazione, ognuno di essi porta con sé una sua componente di incertezza, che egli ‘eredita’ dalla popolazione di cui fa parte. In questo caso, la popolazione ha una varianza pari a \(12^2 = 144\) e quindi ognuno dei tre soggetti campionati eredita tale varianza. Quando calcolo la media di tre osservazioni, in prima battuta io le sommo. A questo punto, dato che si tratta di osservazioni indipendenti, la propagazione degli errori (punto 2) ci dice che la varianza della somma è uguale a \(144 \times 3 = 432\).

Dopo aver sommato, il calcolo della media richiede che il risultato venga diviso per 3. La legge di propagazione degli errori (punto 3) ci dice quindi che la varianza viene divisa per \(3^2 = 9\). Insomma la popolazione delle medie è normale (punto 1), ha media pari a 120 e varianza pari a \(432/9 = 48\) e, di conseguenza, deviazione standard pari a \(\sqrt{48} = 6.928\), cioè \(12/\sqrt{3}\). In generale, l’errore standard di una media è:

\[\sigma_m = \frac{\sigma }{\sqrt n }\]

dove n è la dimensione del campione.

5.3 Riepilogo 1: Caratterizzare l’incertezza di un esperimento

Che cosa ci insegna questo esperimento? Ci insegna che, se prendiamo una distribuzione normale con media \(\mu\) e deviazione standard \(\sigma\) e cominciamo ad estrarre campioni, le medie dei campioni sono variabili, secondo una distribuzione normale con media \(\mu\) e deviazione standard \(\sigma / \sqrt{n}\). Questo concetto è interessante e può essere utilizzato per caratterizzare l’incertezza dei risultati di un esperimento. Riassumiamo:

Abbiamo fatto un esperimento con tre repliche campionando da una distribuzione normale incognita.
Abbiamo ottenuto i tre valori 105.5152, 123.3292 e 133.0133.
In base alle osservazioni in nostro possesso, concludiamo che la concentrazione erbicida è pari a m = 120.6192 \(mg/l\), con una deviazione standard pari a 13.9479 \(mg/l\).
Dobbiamo adottare un atteggiamento prudenziale in relazione alla media, dato che non sappiamo il valore vero di \(\mu\).
Immaginiamo di conoscere la sampling distribution, che avrà una deviazione standard pari a:

sd(Y) / sqrt(3)
## [1] 5.62198

Concludiamo quindi che \(\mu\) è pari a 120.6192 \(\pm\) 8.053

Abbiamo caratterizzato l’incertezza del risultato attraverso un intervallo di valori (stima per intervallo).

5.4 L’intervallo di confidenza

Sarebbe interessante poter rispondere a questa domanda: ”qual è la proporzione di medie (cioè di ipotetici risultati del mio esperimento) che si trova all’interno della fascia di incertezza data?”. Un passo in avanti in questo senso è stato fatto da Neyman (1941), che propose di lavorare con la statistica T, definita come:

\[T = \frac{m - \mu}{\sigma_m}\]

dove \(\sigma_m\) è l’errore standard \(\sigma / \sqrt{n}\). Se \(m\) è distribuito normalmente con media \(\mu\) e deviazione standard \(\sigma\), la legge di propagazione degli errori ci dice che T è distribuito normalmente con media pari a \(m - \mu = 0\) e deviazione standard \(\sigma_m/\sigma_m = 1\). Cioè la sampling distribution di T è una distribuzione normale standardizzata..¹

Quindi possiamo scrivere:

\[ P \left[ \textrm{qnorm}(0.025, 0, 1) \le \frac{m - \mu }{\sigma_m} \le \textrm{qnorm}(0.975, 0, 1) \right] = 0.95 \]

cioè: esiste una probabilità pari a 0.95 che \(T = (m - \mu)/\sigma_m\) è compreso tra il 2.5-esimo e il 97.5-esimo percentile di una distribuzione normale standardizzata. E’ facile vedere che:

qnorm(0.025, 0, 1)
## [1] -1.959964
qnorm(0.975, 0, 1)
## [1] 1.959964

Quindi, approssimando alla seconda cifra decimale:

\[P \left[ -1.96 \le \frac{m - \mu }{\sigma_m} \le 1.96 \right] = 0.95\]

Con semplici passaggi algebrici, possiamo ottenere l’intervallo di confidenza:

\[P \left[ m -1.96 \times \sigma_m \le \mu \le m + 1.96 \times \sigma_m \right] = 0.95\]

Proviamo a leggere l’espressione sovrastante: esiste una probabilità pari a 0.95 che \(\mu\) (la media vera e ignota della popolazione), sia compreso all’interno di due valori che si ottengono sottraendo e aggiungendo alla media del campione \(m\) un multiplo dell’errore standard. Il coefficiente moltiplicativo è circa pari a due.

Il problema è che, nella pratica sperimentale, \(\sigma\) non è noto. Neyman propose di utilizzare \(s\) al posto di \(\sigma\), cioè la deviazione standard del campione, invece che quella della popolazione. Quindi, nel nostro caso, i limiti dell’intervallo di confidenza sono pari a:

m + qnorm(0.025) * s/sqrt(3)
## [1] 104.1788
m + qnorm(0.975) * s/sqrt(3)
## [1] 126.2165

più semplicemente:

m + 2 * s/sqrt(3)
## [1] 126.4416
m + 2 * s/sqrt(3)
## [1] 126.4416

Questo che abbiamo calcolato è l’intervallo di confidenza per P = 0.95. Aumentando opportunamente il moltiplicatore possiamo calcolare gli intervalli di confidenza per P = 0.99, P = 0.999 e così via. Di fatto, l’intervallo di confidenza per P = 0.95 è il più utilizzato in pratica.

5.5 Qual è il senso dell’intervallo di confidenza?

E’ utile ricordare il nostro punto di partenza e il nostro punto di arrivo:

PUNTO DI PARTENZA: una distribuzione normale con \(\mu\) = 120 e \(\sigma\) = 12. Nella realtà assumiamo che la distribuzione di partenza sia normale, mentre i suoi parametri sono totalmente ignoti.
PUNTO DI ARRIVO: una stima di \(\mu\) ed un intervallo di confidenza.

Che cosa significa questo intervallo? Esso fornisce:

una misura di precisione: più piccolo è l’intervallo, maggiore è la precisione della stima;
un’espressione di confidenza nel fatto che, se ripetessimo molte volte l’esperimento, nel 95% dei casi l’intervallo calcolato conterrebbe \(\mu\).

Insomma, l’intervallo di confidenza serve ad esplicitare la nostra incertezza sulla media vera della popolazione in studio.

5.6 Come presentare i risultati degli esperimenti

Dopo aver letto questo capitolo e quelli precedenti, dovrebbe essere chiaro che la presenza dell’errore sperimentale crea incertezza in relazione alle caratteristiche della popolazione da cui abbiamo estratto il campione. Pertanto, è sempre obbligatorio associare alle nostre stime un indicatore di incertezza, la cui assenza non è, in linea di principio, accettabile. Possiamo considerare le seguenti possibilità:

riportare la media associata alla deviazione standard, per descrivere la variabilità originale del fenomeno in studio;
riportare la media associata all’errore standard, per descrivere l’incertezza associata alla stima della media;
riportare l’intervallo di confidenza ottenuto sottraendo/aggiungendo alla media il doppio dell’errore standard, per descrivere l’incertezza associata alla stima della media;

5.7 Alcune precisazioni

5.7.1 Campioni numerosi e non

Calcolare l’intervallo di confidenza utilizzando il doppio dell’errore standard costituisce un’approssimazione che è valida solo quando abbiamo esperimenti con un numero elevato di soggetti (maggiore di 15-20 circa). Per gli esperimenti piccoli, è necessario incrementare opportunamente il moltiplicatore. A questo fine viene utilizzato il valore corrispondente al 97.5-esimo percentile della distribuzione t di Student (non alla normale standardizzata, come abbiamo fatto finora), con un numero di gradi di libertà pari a quelli del campione studiato. Con tre soggetti il moltiplicatore sarebbe:

qt(0.975, 2)
## [1] 4.302653

Il moltiplicatore diminuisce all’aumentare della numerosità e, con 20 soggetti, diviene molto vicino a 2.

qt(0.975, 20)
## [1] 2.085963

Nel nostro esempio, con tre soggetti, l’intervallo di confidenza sarebbe:

m + qt(0.025, 2) * s/sqrt(3)
## [1] 91.00824
m + qt(0.975, 2) * s/sqrt(3)
## [1] 139.3871

Quindi, ben più alto di quello approssimato calcolato in precedenza.

5.7.2 Popolazioni gaussiane e non

In questo esempio siamo partiti da una popolazione con distribuzione gaussiana. In altri casi potrebbe non essere così. Ad esempio, immaginiamo di avere una popolazione di insetti, nella quale il rapporto tra maschi e femmine è ignoto. Campioniamo 40 insetti e contiamo 15 femmine. Qual è la proporzione di femmine nella popolazione originaria?

In questo caso stiamo studiando una grandezza che, almeno nel principio, non può essere gaussiana, ma è binomiale (vedi il capitolo precedente). Nonostante questo, possiamo utilizzare la stessa tecnica per la stima dell’intervallo di confidenza: sappiamo che la media di una distribuzione binomiale è \(p = 14/40 = 0.375\), mentre la deviazione standard è \(\sigma = \sqrt{0.375 \times (1 - 0.375)} = 0.484\)..² Di conseguenza, l’errore standard è \(0.484 / \sqrt{40} = 0.077\). L’intervallo di confidenza sarà dato quindi da:

0.375 - 2 * 0.077
## [1] 0.221
0.375 + 2 * 0.077
## [1] 0.529

Chi fosse interessato ad approfondire questi aspetti può proseguire nella lettura, dopo gli esercizio. Gli altri potranno fermarsi agli esercizi sottostanti.

5.8 Analisi statistica dei dati: riassunto del percorso logico

Considerando quanto finora detto, possiamo riassumere la logica dell’inferenza tradizionale nel modo seguente:

Un esperimento è solo un campione di un numero infinito di esperimenti simili che avremmo potuto/dovuto eseguire, ma che non abbiamo eseguito, per mancanza di risorse;
Assumiamo che i dati del nostro esperimento sono generati da un modello matematico probabilistico, che prende una certa forma algebrica e ne stimiamo i parametri utilizzando i dati osservati;
Costruiamo la sampling distribution per i parametri stimati o per altre statistiche rilevanti, in modo da caratterizzare i risultati delle infinite repliche del nostro esperimento, che avremmo dovuto fare, ma che non abbiamo fatto.
Utilizziamo la sampling distribution per l’inferenza statistica.

5.9 Da ricordare

La natura genera i dati
Noi scegliamo un modello deterministico che simula il meccanismo di generazione dei dati attuato dalla natura.
Stimiamo i parametri.
Confrontiamo le previsioni con i dati osservati. Determiniamo \(\epsilon\) e la sua deviazione standard (\(\sigma\))
Assumiamo un modello stocastico ragionevole per spiegare \(\epsilon\), quasi sempre di tipo gaussiano, con media 0 e deviazione standard pari a \(\sigma\), indipendente dalla X (omoscedasticità)
Qualunque stima sperimentale deve essere associata ad un indicatore di variabilità (errore standard o intervallo di confidenza).

5.10 Esercizi

Un’analisi chimica è stata eseguita in triplicato, ottenendo i seguenti risultati: 125, 169 e 142 ng/g. Calcolare media, devianza, varianza, deviazione standard, coefficiente di variabilità ed errore standard.
Considerare il campione composto dai valori 140 - 170 - 155 e stimare i limiti di confidenza della media (P = 0.95).
Un campione di 400 insetti a cui è stato somministrato un certo insetticida mostra che 136 di essi sono sopravvissuti. Determinare un intervallo di confidenza con grado di fiducia del 95% per la proporzione della popolazione insensibile al trattamento.

Tra tutte le distribuzioni normali, ce n’è una particolare, che ha media 0 e deviazione standard 1. Questa si chiama distribuzione normale standardizzata↩
La distribuzione binomiale è trattata in appendice↩