I am one of those old guys who still uses the stabilising transformations, when the data do not conform to the basic assumptions for ANOVA. Indeed, apart from counts and proportions, where GLMs can be very useful, I have not yet found a simple way to deal with heteroscedasticity for continuous variables, such as yield, weight, height and so on. Yes, I know, Generalised Least Squares (GLS) can be useful to fit heteroscedastic models, but I would argue that stabilising transformations are, conceptually, very much simpler and they can be easily thought to PhD students and practitioners, with only a basic level of knowledge about statistics.
In the recent past, the package emmeans gave me a big boost for its useful way to handle back-transformations. For example, in the box below, I have performed an ANOVA on log-transformed data and retrieved the back-transformed means on the original count scale.
library(emmeans)
fileName <- "http://www.casaonofri.it/_datasets/insects.csv"
dataset <- read.csv(fileName)
head(dataset)
## Insecticide Rep Count
## 1 T1 1 448
## 2 T1 2 906
## 3 T1 3 484
## 4 T1 4 477
## 5 T1 5 634
## 6 T2 1 211
r
model <- lm(log(Count) ~ Insecticide, data = dataset)
emmeans(model, ~Insecticide, type = "response")
## Insecticide response SE df lower.CL upper.CL
## T1 568.6 101.01 12 386.1 837.3
## T2 335.1 59.54 12 227.6 493.5
## T3 51.9 9.22 12 35.2 76.4
##
## Confidence level used: 0.95
## Intervals are back-transformed from the log scale
It is very simple: emmeans auto-detects the transformation function (which is made inside the model specification) and automatically produces the back-transformation, when this is requested by using the ‘type = "response"’ argument (we can also use the argument ‘regrid = "response"’, with slight differences that I will discuss in a future post).
Unfortunately, not all transformations are auto-detected; for example, let’s consider the dataset ‘Hours_to_failure.csv’, where we have the time-to-failure (in hours) for a device, as affected by the operating temperature. If we regard the temperature as a factor, we can fit an ANOVA model; a check with the boxcox() function in the MASS package suggests that this dataset might require a stabilising transformation into the inverse value.
library(MASS)
library(emmeans)
fileName <- "http://www.casaonofri.it/_datasets/Hours_to_failure.csv"
dataset <- read.csv(fileName)
dataset$Temp <- factor(dataset$Temp)
head(dataset)
## Temp Hours_to_failure
## 1 1520 1953
## 2 1520 2135
## 3 1520 2471
## 4 1520 4727
## 5 1520 6134
## 6 1520 6314
r
model <- lm(Hours_to_failure ~ Temp, data = dataset)
tp <- boxcox(model)
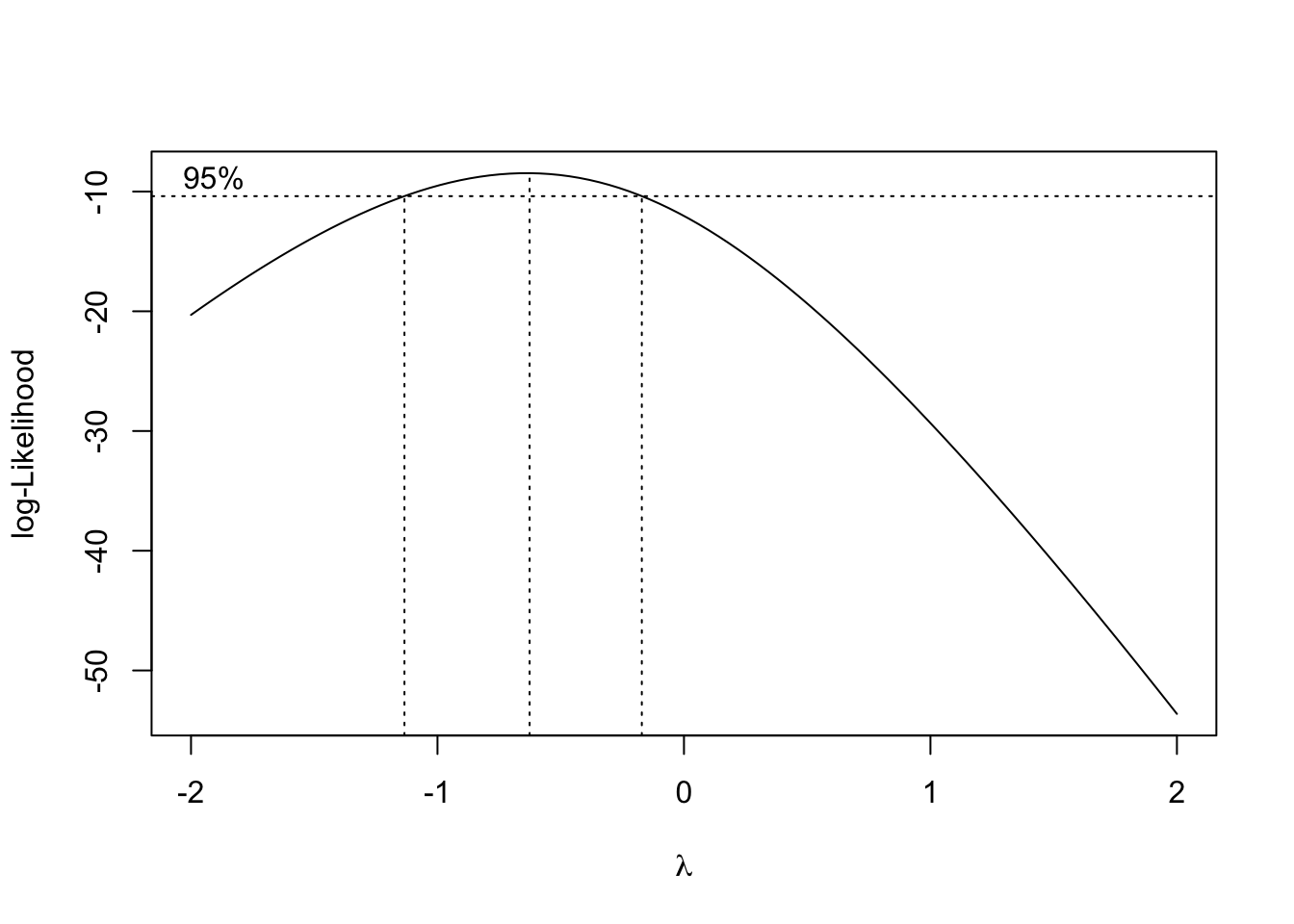
As we see below, the inverse transformation is not auto-detected.
model2 <- lm(I(1/Hours_to_failure) ~ Temp, data = dataset)
emmeans(model2, ~ Temp, type = "response")
## Temp response SE df lower.CL upper.CL
## 1520 0.000320 9.52e-05 20 0.000121 0.000518
## 1620 0.000579 9.52e-05 20 0.000381 0.000778
## 1660 0.001043 9.52e-05 20 0.000844 0.001241
## 1708 0.001565 9.52e-05 20 0.001366 0.001763
##
## Confidence level used: 0.95
## Intervals are back-transformed from the identity scale
In this situation, an alternative approach must be used. The transformation can be made prior to fitting the model; next, we need to update the ‘reference grid’ for the model, specifying what type of transformation we have made (tran = "inverse"). Finally, we can pass the updated grid into the emmeans() function. And … the back-transformation is served!
dataset$invHours <- 1/dataset$Hours_to_failure
model3 <- lm(invHours ~ Temp, data = dataset)
updGrid <- update(ref_grid(model3), tran = "inverse")
emmeans(updGrid, ~Temp, type = "response")
## Temp response SE df lower.CL upper.CL
## 1520 3128 931.6 20 1930 8258
## 1620 1726 283.6 20 1285 2626
## 1660 959 87.6 20 806 1185
## 1708 639 38.9 20 567 732
##
## Confidence level used: 0.95
## Intervals are back-transformed from the inverse scale
I can use this method with several functions, such as: “identity”, “1/mu^2”, “inverse”, “reciprocal”, “log10”, “log2”, “asin.sqrt”, and “asinh.sqrt”.
Sometimes, I need extra-flexibility. For example, if we look at ‘boxcox’ graph above, we see that the inverse transformation, although acceptable (the value \(-1\) is within the confidence limits for \(\lambda\)) is not the best one. Indeed, the maximum likelihood value is -0.62:
tp$x[which.max(tp$y)]
## [1] -0.6262626
Therefore, we might like to use the following transformation, that is within the ‘boxcox’ family:
$$W = \frac{Y^{-0.62} - 1}{-0.62}$$
This type of transformation is not manageable with the previous code and we need to use the make.tran() function, specifying the value of \(\lambda\) (alpha = -0.62) and the value of the displacement parameter (beta = 1).
dataset$bcHours <- (dataset$Hours_to_failure^(-0.62) - 1)/(-0.62)
model4 <- lm(bcHours ~ Temp, data = dataset)
updGrid <- update(ref_grid(model4),
tran = make.tran("boxcox", alpha = -0.62,
beta = 1))
emmeans(updGrid, ~Temp, type = "response")
## Temp response SE df lower.CL upper.CL
## 1520 3265 708.8 20 2191 5556
## 1620 1763 260.9 20 1329 2483
## 1660 976 100.0 20 798 1227
## 1708 642 50.7 20 549 764
##
## Confidence level used: 0.95
## Intervals are back-transformed from the Box-Cox (lambda = -0.62) of (y - 1) scale
The function make.tran() can be used to specify several other transformation functions, such as the angular transformation that is often used for percentages and proportions. You can get a full list by searching help ('?make.tran') from inside R.
In conclusion, stabilising transformations, in spite of their age, can still be useful to fit heteroscedastic models; do not underrate them, just because they are no longer in fashion!
Thanks for reading!
Prof. Andrea Onofri
Department of Agricultural, Food and Environmental Sciences
University of Perugia (Italy)
Send comments to: andrea.onofri@unipg.it