Principal Component Analysis (PCA) is perhaps the most widespread multivariate technique in biology and it is used to summarise the results of experiments in a wide range of disciplines, from agronomy to botany, from entomology to plant pathology. Whenever possible, the results are presented by way of a biplot, an ubiquitous type of graph with a formidable descriptive value. Indeed, carefully drawn biplots can be used to represent, altogether, the experimental subjects, the experimental variables and their reciprocal relationships (distances and correlations).
However, biplots are not created equal and the interpretational rules may change dramatically, depending on how the data were processed. As a reviewer/editor, I often feel that the authors have perfomed their Principal Component Analyses by using the default options in their favourite R function, but they are not totally aware of how the data were processed to reach the final published result. Therefore, their interpretation of biplots is, sometimes, more or less abused.
I thought that it might be helpful to offer a ‘user-friendly’ explanation of the basic interpretational rules for biplots, with no overwhelming mathematical detail.
A simple example
Let’s look at a simple (perhaps too simple), but realistic example. This is an herbicide trial, where we compared weed control ability of nine sugarbeet herbicides. Ground covering for six weed species was recorded; the weed species were Polygonum lapathyfolium, Chenopodium polyspermum, Echinochloa crus-galli, Amaranthus retroflexus, Xanthium strumarium and Polygonum aviculare; they were identified by using their BAYER code (the first three letters of the genus name and the first two letters of the species name). The aim of the experiment was to ordinate herbicide treatments in terms of their weed control spectra.
The dataset is available in an online repository (see below). It is a dataframe, although we’d better convert it into the matrix \(X\) for further analyses.
WeedPop <- read.csv("https://www.statforbiology.com/_data/WeedPop.csv",
header = T)
X <- WeedPop[,2:7]
row.names(X) <- WeedPop[,1]
X
## POLLA CHEPO ECHCG AMARE XANST POLAV
## A 0.1 33 11 0 0.1 0.1
## B 0.1 3 3 0 0.1 0.0
## C 7.0 19 19 4 7.0 1.0
## D 18.0 3 28 19 12.0 6.0
## E 5.0 7 28 3 10.0 1.0
## F 11.0 9 33 7 10.0 6.0
## G 8.0 13 33 6 15.0 15.0
## H 18.0 5 33 4 19.0 12.0
## I 6.0 6 38 3 10.0 6.0Now, let’s submit the matrix X to a PCA, by using the default options in the prcomp() function. In this case, the data is centered prior to analyses, but it is not standardised to unit variance.
As the results, we obtain two matrices, that we will call G and E; they respectively contain the subject-scores (or principal component scores) and the trait-scores (this is the rotation matrix). These two matrices, by multiplication, return the original centered data matrix.
pcaMod <- prcomp(X)
G <- pcaMod$x
E <- pcaMod$rotation
print(G, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## A -26.97 12.2860 3.129 0.271 -0.00398 0.581
## B -20.81 -17.3167 -2.935 -3.081 -1.29287 0.475
## C -9.95 3.6671 3.035 0.819 2.38378 -0.801
## D 12.69 -7.3364 11.756 3.732 -1.45392 -0.180
## E 1.13 -2.2854 -5.436 3.412 1.86926 -2.247
## F 8.05 1.6470 -0.455 2.895 0.22101 1.607
## G 9.46 7.3174 -1.213 -5.072 -4.98975 -0.976
## H 16.34 0.0632 0.799 -7.213 4.07606 0.509
## I 10.07 1.9578 -8.680 4.237 -0.80960 1.032
print(E, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## POLLA 0.349 -0.0493 0.5614 -0.1677 0.5574 0.4710
## CHEPO -0.390 0.8693 0.2981 -0.0013 0.0480 -0.0327
## ECHCG 0.688 0.4384 -0.3600 0.4322 -0.0113 0.1324
## AMARE 0.213 -0.1200 0.6808 0.4155 -0.4893 -0.2547
## XANST 0.372 0.1050 0.0499 -0.4107 0.2631 -0.7813
## POLAV 0.263 0.1555 0.0184 -0.6662 -0.6150 0.2903
print(G %*% t(E), digits = 3)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## A -8.033 22.11 -14.11 -5.111 -9.144 -5.133
## B -8.033 -7.89 -22.11 -5.111 -9.144 -5.233
## C -1.133 8.11 -6.11 -1.111 -2.244 -4.233
## D 9.867 -7.89 2.89 13.889 2.756 0.767
## E -3.133 -3.89 2.89 -2.111 0.756 -4.233
## F 2.867 -1.89 7.89 1.889 0.756 0.767
## G -0.133 2.11 7.89 0.889 5.756 9.767
## H 9.867 -5.89 7.89 -1.111 9.756 6.767
## I -2.133 -4.89 12.89 -2.111 0.756 0.767Biplot and interpretational rules
We can draw a biplot by using the first two columns in G for the markers and the first two columns in E for the arrowtips. In the box below I used the biplot.default() method in R; I decided not to use the biplot.prcomp() method, in order to avoid any further changes in G and E.
biplot(G[,1:2], E[,1:2], xlab="PC1 (64%)",
ylab="PC2 (16%)", main = "Default biplot \n\n")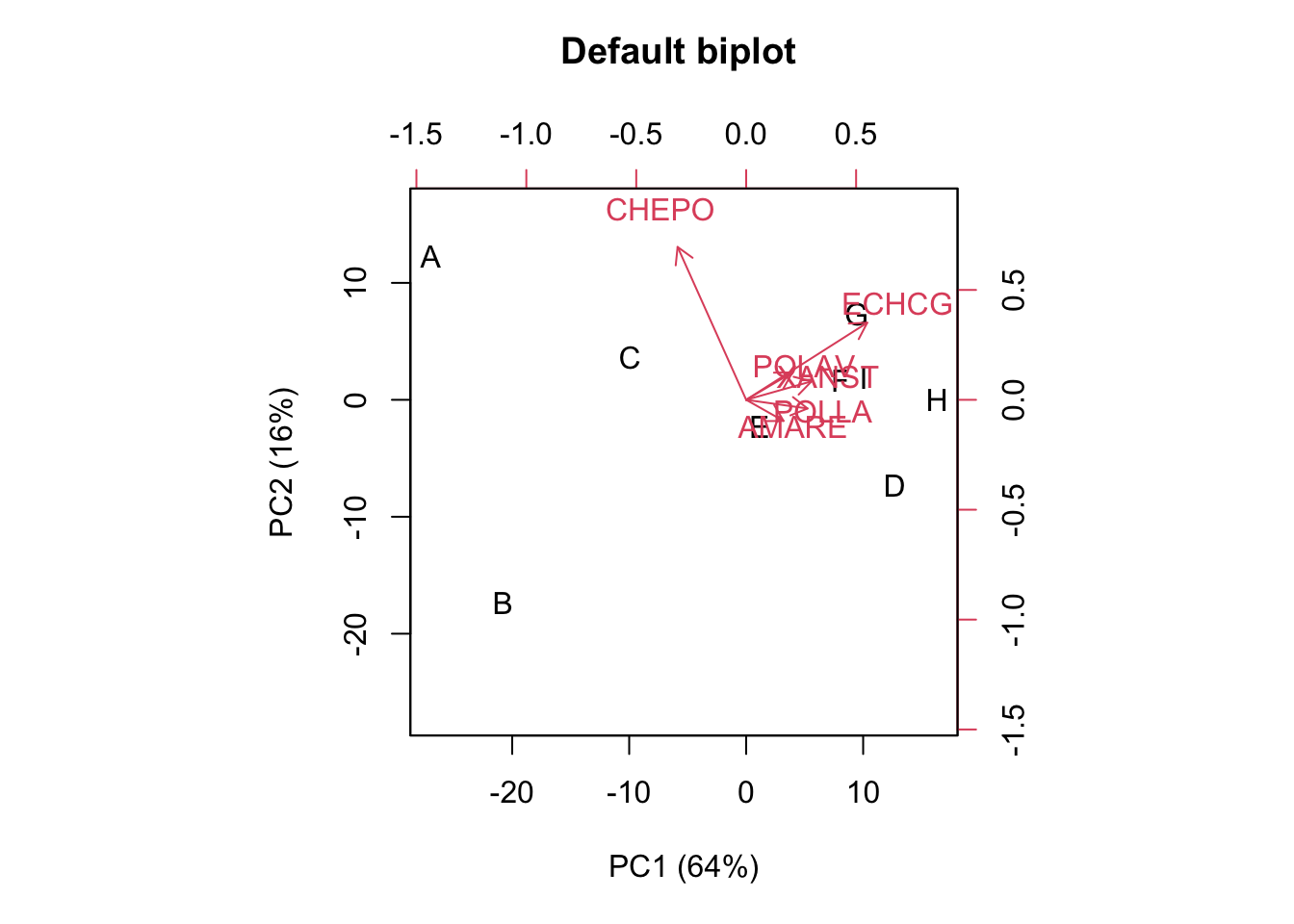
Yes, I know, the biplot does not look nice for publication (but, better solutions with ‘ggplot’ exist! Google for them!). Please, note that the markers are the experimental subjects and the arrows are the observed variables, which is the most common choice.
The interpretational rules are based on:
- the distances between markers;
- the distances from markers to the origin of axes;
- the lengths of arrows;
- the angles between arrows;
- the relative positions of arrows;
- the relative positions of arrows and markers.
By looking at those six characteristics, we should be able to derive information on:
- the similarity of objects;
- the existence of groupings;
- the contribution of the experimental variables to the observed groupings;
- the relationship between experimental variables;
- the original value of each subject in each variable.
What is the problem, then? The problem is that, depending on how the data were processed during the PCA, we obtain different types of biplots, conveying different information. Therefore, the interpretational rules muxt change according to the type of biplot.
The possible options for PCA
During my lecturing activities I have noted that most PhD students are perfectly aware that, prior to PCA, we have the options of either:
- centering the data, or
- standardising them.
In general, students are also aware that such a first decision impacts on the results of a PCA and on their interpretation.
What it is less known is that, independent on data transformation, the results of a PCA are not unique, but they may change, depending on how the calculations are performed. Indeed, with a PCA, we look for two appropriate matrices, which:
- allow for the best description of our dataset in reduced rank space and
- by multiplication return the original centered or standardised data matrix (i.e. \(Y = G \, E^T\)).
By using the default options in prcomp(), we have found G and E, but there is an infinite number of matrix couples that obey the two requirements above. These couples can be found by ‘scaling’ G and E, according to our specific research needs. What does ‘scaling’ mean? It is easy: the columns of G and E can be, respectively, multiplied and divided by some selected constant values, to obtain two new matrices, that also represent an acceptable solution to a PCA, as long as their product returns the original data matrix.
Let’s see the most common types of scalings.
Scaling 1
If we take G and E the way they are, with no changes, we say that we are using the so called Scaling 1, that is, by far, the the most common type of scaling and it is also know as Principal Component Scaling or row-scaling. Let’s have a closer look at the columns of G and E and, for each column, we calculate the norm (sum of squared elements):
# norms of column-vectors in G
normsG <- sqrt(diag(crossprod(G)))
normsG
## PC1 PC2 PC3 PC4 PC5 PC6
## 44.091847 24.153689 16.523462 11.827405 7.428198 3.338675
# norms of column-vectors in E
normsE <- sqrt(diag(crossprod(E)))
normsE
## PC1 PC2 PC3 PC4 PC5 PC6
## 1 1 1 1 1 1We see that, with scaling 1, the column-vectors in E have unit norms, while the column-vectors in G have positive and decreasing norms.
Scaling 2
If we divide each column in G for the respective column-norm, we obtain a new G2 matrix, with column-norms equal to unity. At the same time, if we multiply each column in E for the same amount, we obtain a new E2 matrix, where the column norms are the same as the column norms of G. We do this scaling, by using the sweep() function and we also show that G2 and E2, by matrix multiplication, return the original centered data matrix (and so, they are an acceptable solution for a PCA).
This second scaling is known as Scaling 2 or column-scaling; it is less common, but, nonetheless, it is the default in the summary.rda() method in the ‘vegan’ package.
# Scaling 2
G2 <- sweep(G, 2, normsG, "/")
E2 <- sweep(E, 2, normsG, "*")
round(G2, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## A -0.612 0.509 0.189 0.023 -0.001 0.174
## B -0.472 -0.717 -0.178 -0.260 -0.174 0.142
## C -0.226 0.152 0.184 0.069 0.321 -0.240
## D 0.288 -0.304 0.711 0.316 -0.196 -0.054
## E 0.026 -0.095 -0.329 0.288 0.252 -0.673
## F 0.183 0.068 -0.028 0.245 0.030 0.481
## G 0.214 0.303 -0.073 -0.429 -0.672 -0.292
## H 0.371 0.003 0.048 -0.610 0.549 0.152
## I 0.228 0.081 -0.525 0.358 -0.109 0.309
round(E2, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## POLLA 15.383 -1.191 9.277 -1.983 4.141 1.572
## CHEPO -17.193 20.997 4.925 -0.015 0.357 -0.109
## ECHCG 30.349 10.589 -5.948 5.112 -0.084 0.442
## AMARE 9.373 -2.899 11.250 4.914 -3.634 -0.850
## XANST 16.387 2.537 0.824 -4.858 1.954 -2.609
## POLAV 11.594 3.757 0.305 -7.879 -4.569 0.969
sqrt(diag(crossprod(G2)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 1 1 1 1 1 1
sqrt(diag(crossprod(E2)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 44.091847 24.153689 16.523462 11.827405 7.428198 3.338675
round(G2 %*% t(E2), digits = 3)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## A -8.033 22.111 -14.111 -5.111 -9.144 -5.133
## B -8.033 -7.889 -22.111 -5.111 -9.144 -5.233
## C -1.133 8.111 -6.111 -1.111 -2.244 -4.233
## D 9.867 -7.889 2.889 13.889 2.756 0.767
## E -3.133 -3.889 2.889 -2.111 0.756 -4.233
## F 2.867 -1.889 7.889 1.889 0.756 0.767
## G -0.133 2.111 7.889 0.889 5.756 9.767
## H 9.867 -5.889 7.889 -1.111 9.756 6.767
## I -2.133 -4.889 12.889 -2.111 0.756 0.767Scaling 3
With scaling 1, the the values in G were, on average, much higher than the values in E; otherwise, with scaling 2, the situation was reversed. In order to have the two matrices in comparable scales, we could think of dividing each column in G for the square root of the respective column-norm and, at the same time, multiply each column in E for the same amount. The two new matrices G3 and E3 have the same column norms (they are now in comparable scales) and, by multiplication, they return the original centered data matrix.
This scaling is known as symmetrical-scaling; it is common in several applications of PCA, such as AMMI and GGE analyses for the evaluation of the stability of genotypes.
# Scaling 3
G3 <- sweep(G, 2, sqrt(normsG), "/")
E3 <- sweep(E, 2, sqrt(normsG), "*")
round(G3, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## A -4.062 2.500 0.770 0.079 -0.001 0.318
## B -3.134 -3.523 -0.722 -0.896 -0.474 0.260
## C -1.498 0.746 0.747 0.238 0.875 -0.438
## D 1.910 -1.493 2.892 1.085 -0.533 -0.099
## E 0.170 -0.465 -1.337 0.992 0.686 -1.230
## F 1.212 0.335 -0.112 0.842 0.081 0.880
## G 1.424 1.489 -0.298 -1.475 -1.831 -0.534
## H 2.460 0.013 0.197 -2.097 1.496 0.279
## I 1.516 0.398 -2.135 1.232 -0.297 0.565
round(E3, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## POLLA 2.317 -0.242 2.282 -0.577 1.519 0.861
## CHEPO -2.589 4.272 1.212 -0.004 0.131 -0.060
## ECHCG 4.570 2.155 -1.463 1.486 -0.031 0.242
## AMARE 1.412 -0.590 2.768 1.429 -1.334 -0.465
## XANST 2.468 0.516 0.203 -1.412 0.717 -1.428
## POLAV 1.746 0.764 0.075 -2.291 -1.676 0.530
sqrt(diag(crossprod(G3)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 6.640169 4.914640 4.064906 3.439099 2.725472 1.827204
sqrt(diag(crossprod(E3)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 6.640169 4.914640 4.064906 3.439099 2.725472 1.827204
round(G3 %*% t(E3), digits = 3)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## A -8.033 22.111 -14.111 -5.111 -9.144 -5.133
## B -8.033 -7.889 -22.111 -5.111 -9.144 -5.233
## C -1.133 8.111 -6.111 -1.111 -2.244 -4.233
## D 9.867 -7.889 2.889 13.889 2.756 0.767
## E -3.133 -3.889 2.889 -2.111 0.756 -4.233
## F 2.867 -1.889 7.889 1.889 0.756 0.767
## G -0.133 2.111 7.889 0.889 5.756 9.767
## H 9.867 -5.889 7.889 -1.111 9.756 6.767
## I -2.133 -4.889 12.889 -2.111 0.756 0.767Scaling 4
Scaling 4 is similar to scaling 2, but the matrix G, instead of to unit norm, is scaled to unit variance, by dividing each column by the corresponding standard deviation. Likewise, E is multiplied by the same amounts, so that E4 has column norms equal to the standard deviations of G. The two matrices G4 and E4, by multiplication, return the original centered matrix.
This scaling is rather common in some applications of PCA, such as factor analysis; the elements in G4 are known as factor scores, while those in E4 are the so-called loadings. It is available, e.g., in the dudi.pca() function in the ‘ade4’ package.
# Scaling 4
G4 <- sweep(G, 2, apply(G, 2, sd), "/")
E4 <- sweep(E, 2, apply(G, 2, sd), "*")
round(G4, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## A -1.730 1.439 0.536 0.065 -0.002 0.492
## B -1.335 -2.028 -0.502 -0.737 -0.492 0.402
## C -0.638 0.429 0.519 0.196 0.908 -0.678
## D 0.814 -0.859 2.012 0.893 -0.554 -0.153
## E 0.073 -0.268 -0.930 0.816 0.712 -1.904
## F 0.516 0.193 -0.078 0.692 0.084 1.362
## G 0.607 0.857 -0.208 -1.213 -1.900 -0.827
## H 1.048 0.007 0.137 -1.725 1.552 0.431
## I 0.646 0.229 -1.486 1.013 -0.308 0.874
round(E4, digits = 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## POLLA 5.439 -0.421 3.280 -0.701 1.464 0.556
## CHEPO -6.079 7.424 1.741 -0.005 0.126 -0.039
## ECHCG 10.730 3.744 -2.103 1.807 -0.030 0.156
## AMARE 3.314 -1.025 3.977 1.737 -1.285 -0.301
## XANST 5.794 0.897 0.291 -1.717 0.691 -0.922
## POLAV 4.099 1.328 0.108 -2.786 -1.615 0.343
apply(X, 2, var)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 43.45750 95.11111 136.86111 32.61111 38.73528 29.06500
sqrt(diag(crossprod(G4)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 2.828427 2.828427 2.828427 2.828427 2.828427 2.828427
sqrt(diag(crossprod(E4)))
## PC1 PC2 PC3 PC4 PC5 PC6
## 15.588822 8.539619 5.841926 4.181619 2.626265 1.180400
round(G4 %*% t(E4), digits = 3)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## A -8.033 22.111 -14.111 -5.111 -9.144 -5.133
## B -8.033 -7.889 -22.111 -5.111 -9.144 -5.233
## C -1.133 8.111 -6.111 -1.111 -2.244 -4.233
## D 9.867 -7.889 2.889 13.889 2.756 0.767
## E -3.133 -3.889 2.889 -2.111 0.756 -4.233
## F 2.867 -1.889 7.889 1.889 0.756 0.767
## G -0.133 2.111 7.889 0.889 5.756 9.767
## H 9.867 -5.889 7.889 -1.111 9.756 6.767
## I -2.133 -4.889 12.889 -2.111 0.756 0.767In conclusion to this section, although we might think that two plus two is always four, unfortunately, this is not true for a PCA and we need to be aware that there are, at least, four types of possible results, depending on which type of scaling has been used for the PC scores in G and the rotation matrix E. Consequently, there are four types of biplots, as we will see in the next section.
Four types of biplots
We have at hand four matrices for the subject-scors (G, G2. G3 and G4) and four matrices for the trait-scores (E, E2, E3 and E4). If we draw a biplot by using the scores in G for the markers and the scores in E for the arrowtips, we obtain the so-called distance biplot.
Otherwise, if we use G2 and E2, we get the so-called correlation biplot. Again, If we use G3 and E3 we obtain a symmetrical biplot, while,if we use G4 and E4 we obtain a further type of biplot, which we could name type 4 biplot.
The four types of biplots are drawn in the following graph.
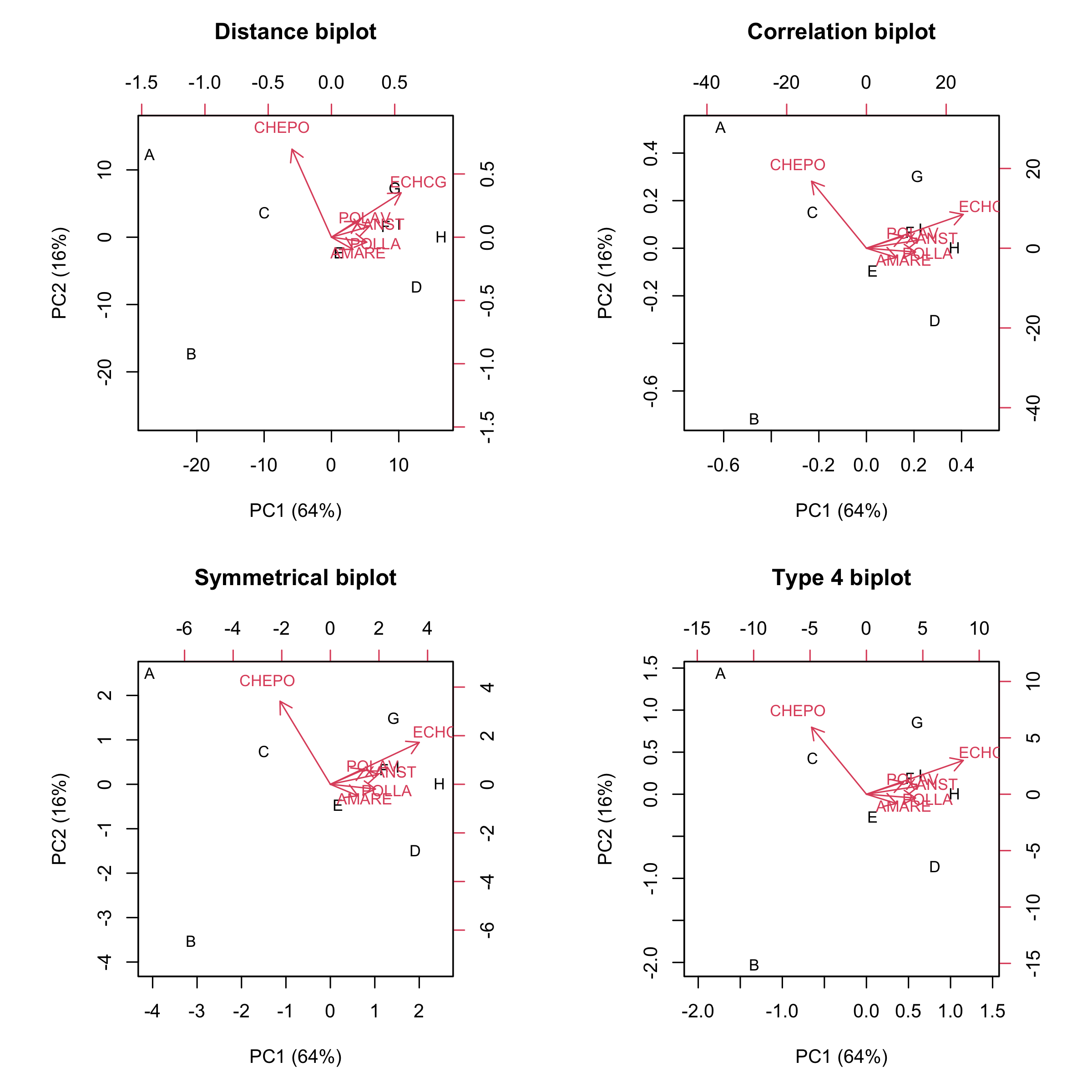
Let’s see how we can interpret the above biplots, depending on the scaling. For those of you who would not like to wait ’till the end of this post to grasp the interpretational rules, I have decided to anticipate the table below.
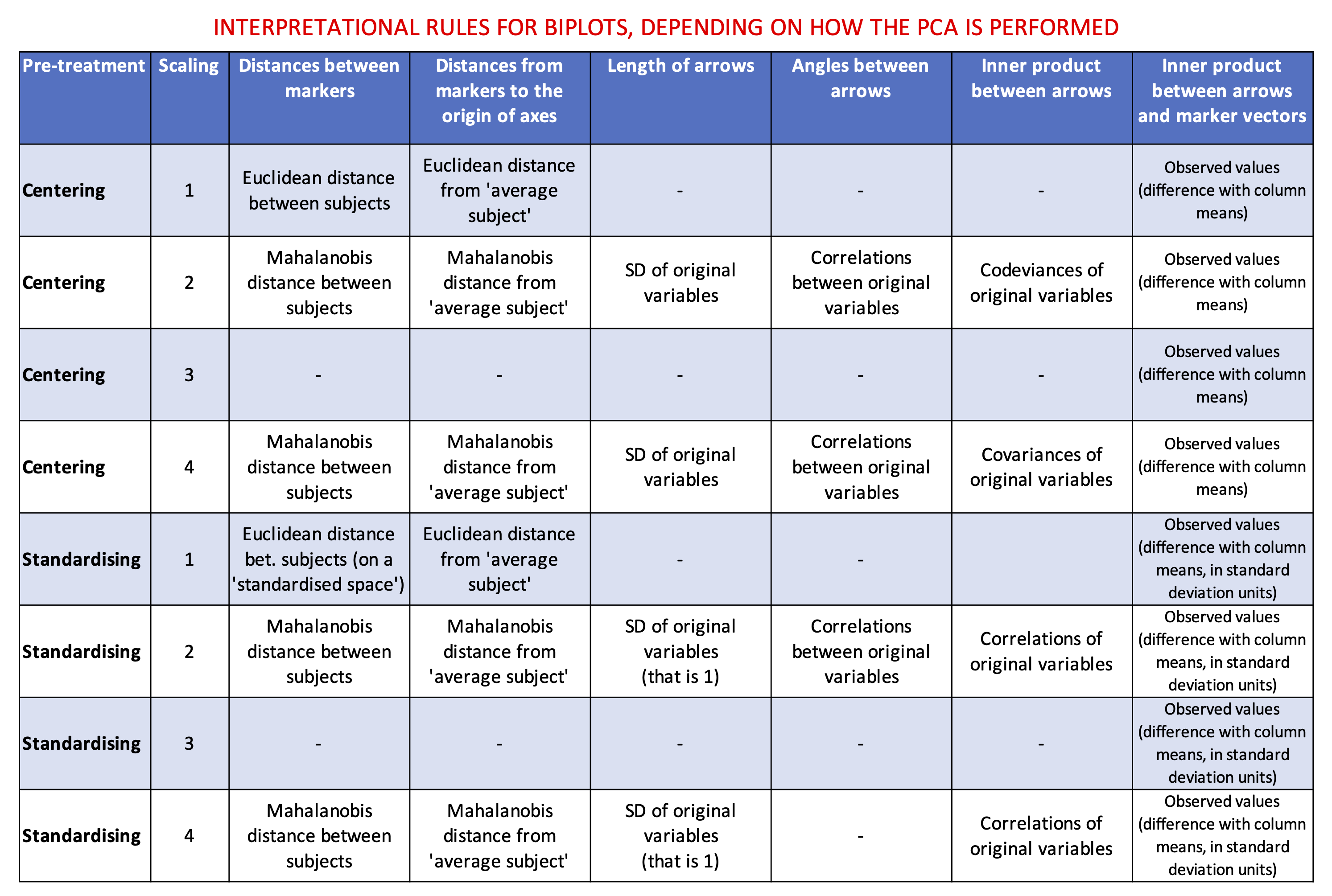
Some preliminary knowledge
At the beginning I promised no overwhelming math detail, but there is one thing that cannot be avoided. If you are totally allergic to math, you can skip this section and only read the final sentence. However, I suggest that you sit back, relax and patiently read through this part.
The whole interpretation of biplots depends from the concept of inner product, which I will try to explain below. We have seen that the results of a PCA come in the form of the two matrices G and E; each row of G corresponds to a marker, while each row of E corresponds to an arrow. We talk about row-vectors. Obviously, as we have to plot in 2D we only take the first two elements in each row-vector, but, if we could plot in 6D, we could draw markers and arrows by taking all six elements in each row-vector.
Now, let’s imagine two row-vectors, named \(u\) and \(v\), with, respectively, co-ordinates equal to [1, 0.25] and [0.25, 1]. I have reported these two vectors as arrows in the graph below and I have highlighted the angle between the two arrows, that is \(\theta\). Furthermore, I have drawn the projection of \(v\) on \(u\), as the segment OA.
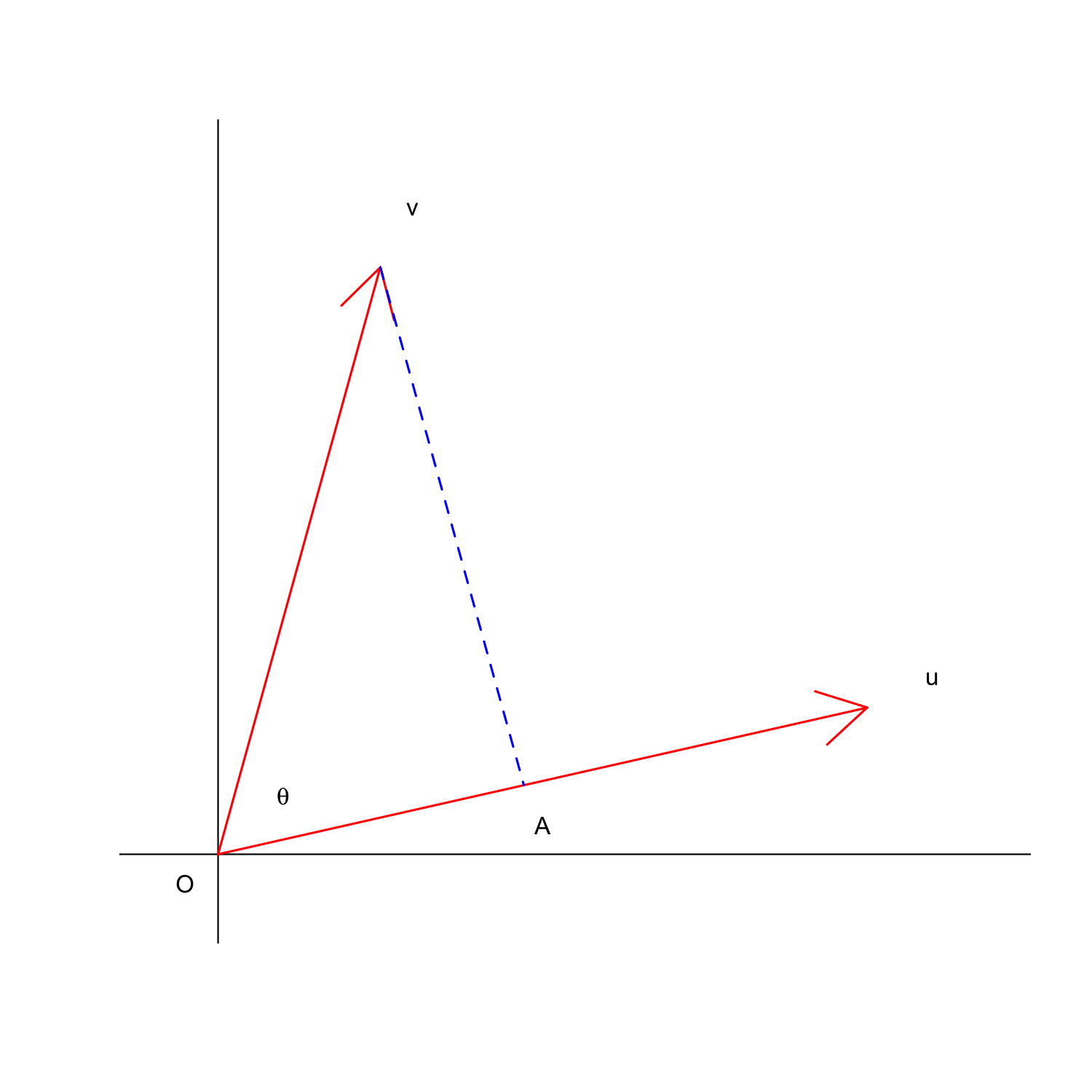
Now, we can use the co-ordinates of \(u\) and \(v\) as row-vectors in the matrix M, so that we have a connection between the graph and the matrix.
M <- matrix(c(0.25, 1, 1, 0.25), 2, 2, byrow = T)
row.names(M) <- c("u", "v")
M
## [,1] [,2]
## u 0.25 1.00
## v 1.00 0.25The inner product \(u \cdot v\) is defined as the sum of the products of coordinates:
\[u \cdot v = (0.25 \times 1) + (1 \times 0.25) = 0.5\]
Obviously, the inner product of a vector with itself is:
\[u \cdot u = |u|^2 = 0.25^2 + 1^2 = 1.0625\]
If we think of the Pythagorean theorem, we immediatly see that such a ‘self inner product’ corresponds to the squared ‘length’ of the arrow (that is the squared norm of the vector). With R, we can obtain the inner products for rows, in a pairwise fashion, by using the tcrossprod() function:
tcrossprod(M)
## u v
## u 1.0625 0.5000
## v 0.5000 1.0625Please, note that the squared norms of the two row-vectors are found along the diagonal. Please, also note that the inner products for column-vectors could be obtained by using the crossprod() function.
Now, how do we visualize the inner product on the graph? By using the cosine inequality, it is possible to demonstrate that:
\[u \cdot v = |u| \, |v| \, cos \theta\]
In words: the inner product of two vectors \(u\) and \(v\) is equal to the product of their lengths \(u\) and \(v\) by the cosine of the angle between them. For an explanation of this, you can follow this link to a nice YouTube tutorial.
This is a very useful property; look at the plot above: you may remember from high school that, in a rectangular triangle, the length of OA (one cathetus) can be obtained by multiplying the length of \(v\) (the hypothenus) by the cosine of \(\theta\).
Therefore:
\[u \cdot v = \overline{OA} \, |v|\]
In words: the inner product between two arrows can be visualised by multiplying the length of one arrow for the length of the projection of the other arrow on the first arrow.
The inner product is also useful to calculate the angle between two vectors; indeed, considering the equation above, we can also write:
\[\cos \theta = \frac{u \cdot v}{|u| \, |v|}\]
Therefore, if we take the matrix M, we can calculate the cosines of the angles between the row-vectors, by using the following code:
cosAngles <- function(mat){
innerProd <- tcrossprod(mat)
norms <- apply(mat, 1, norm, type = "2")
sweep(sweep(innerProd, 2, norms, "/"), 1, norms, "/")
}
cosAngles(M)
## u v
## u 1.0000000 0.4705882
## v 0.4705882 1.0000000Obviously, the angle of a vector with itself is 0 and its cosine is 1.
As conclusions to this section, please note the following.
- The inner product between two arrows (or between an arrow and a subject-marker) can be visualised by multiplying the length of one arrow for the length of the projection of the other arrow on the first arrow
- The squared length of an arrow, or the squared distance from a marker and the origin of axes, is obtained by summing the squares of its co-ordinates
Interpretational rules for biplots
Rule 1: Distances between markers
The Euclidean distances between subjects in the original X matrix can be regarded as measures of dissimilarity. They can be calculated by using the following code:
dist(X)
## A B C D E F G
## B 31.048510
## C 19.288079 24.984395
## D 45.241905 38.522980 27.073973
## E 33.118424 27.803237 15.459625 21.679483
## F 36.886718 35.182666 18.841444 16.062378 10.295630
## G 37.768108 39.311830 22.293497 22.000000 17.320508 11.489125
## H 45.860986 41.732721 27.892651 18.411953 20.024984 13.820275 13.892444
## I 40.430558 37.574193 23.790755 22.649503 11.269428 8.660254 13.892444
## H
## B
## C
## D
## E
## F
## G
## H
## I 16.970563If we consider the matrices G, G2, G3 and G4, we see that only the first one preserves the Euclidean inter-object distances (the box below shows only the distances between the subject ‘I’ and all other subjects, for the sake of brevity):
as.matrix(dist(G))[9,]
## A B C D E F G H
## 40.430558 37.574193 23.790755 22.649503 11.269428 8.660254 13.892444 16.970563
## I
## 0.000000
as.matrix(dist(G2))[9,] # Proportional to mahalanobis
## A B C D E F G H
## 1.2416395 1.2894994 1.1327522 1.3499172 1.0999901 0.5584693 1.2454512 1.3227711
## I
## 0.0000000
as.matrix(dist(G3))[9,] # Not proportional
## A B C D E F G H
## 6.741577 6.606727 4.569223 5.433575 2.727196 2.141145 3.931517 4.567013
## I
## 0.000000
as.matrix(dist(G4))[9,] # Mahlanobis
## A B C D E F G H
## 3.511887 3.647255 3.203907 3.818143 3.111242 1.579590 3.522668 3.741362
## I
## 0.000000This leads us to the first interpretational rule: starting from a column-centered matrix, with a distance biplot (scaling 1), the Euclidean distances between markers approximate the Euclidean distances between subjects in the original centered matrix. Instead, with scaling 2 and 4 the Euclidean distances between markers approximate the Mahalanobis distances of subjects, which represent a totally different measure of dissimilarity.
Rule 2: Distances from markers to the origin of axes
Let’s now consider the distance of each marker from the origin of the axes. We need to consider that a hypothetical subject with average values for all original variables would be located exactly on the origin of axes, independent on the scaling. Therefore, the distance from the origin of axes shows how far is that subject from the hypothetical ‘average subject’: the farthest the distance, the most ‘notable’ the subject (very high or very low), in relation to one or more of the original variables.
Therefore, the second interpretational rule is: starting from a column-centered matrix, independent from scaling, the Euclidean distance between a marker and the origin approximate the dissimilarity between a subject and a hypothetical subject that has average value for all original variables. With scaling 1, such dissimilarity is measured by the Euclidean distance, while with scalings 2 and 4, it is measured by the Mahalanobis distance.
Rule 3 and 4: Lengths of arrows and inner products
We have seen that the pairwise inner products of row vectors in a matrix can be obtained by using the tcrossprod() function. In this respect, the inner products of row-vectors E1 and E3 (scaling 1 and 3) are totally meaningless. On the other hand, the inner products for row vectors in E2 and E4 represent, respectively, the deviances-codeviances and variance-covariances of the original observations in X.
tcrossprod(E2)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## POLLA 347.6600 -242.4667 389.2667 225.86667 270.3267 174.93000
## CHEPO -242.4667 760.8889 -328.8889 -167.88889 -223.3556 -120.56667
## ECHCG 389.2667 -328.8889 1094.8889 211.88889 493.1556 350.36667
## AMARE 225.8667 -167.8889 211.8889 260.88889 126.7556 78.26667
## XANST 270.3267 -223.3556 493.1556 126.75556 309.8822 226.59667
## POLAV 174.9300 -120.5667 350.3667 78.26667 226.5967 232.52000
tcrossprod(E4)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## POLLA 43.45750 -30.30833 48.65833 28.233333 33.79083 21.866250
## CHEPO -30.30833 95.11111 -41.11111 -20.986111 -27.91944 -15.070833
## ECHCG 48.65833 -41.11111 136.86111 26.486111 61.64444 43.795833
## AMARE 28.23333 -20.98611 26.48611 32.611111 15.84444 9.783333
## XANST 33.79083 -27.91944 61.64444 15.844444 38.73528 28.324583
## POLAV 21.86625 -15.07083 43.79583 9.783333 28.32458 29.065000
cov(X)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## POLLA 43.45750 -30.30833 48.65833 28.233333 33.79083 21.866250
## CHEPO -30.30833 95.11111 -41.11111 -20.986111 -27.91944 -15.070833
## ECHCG 48.65833 -41.11111 136.86111 26.486111 61.64444 43.795833
## AMARE 28.23333 -20.98611 26.48611 32.611111 15.84444 9.783333
## XANST 33.79083 -27.91944 61.64444 15.844444 38.73528 28.324583
## POLAV 21.86625 -15.07083 43.79583 9.783333 28.32458 29.065000Consequently, the lengths of arrows (norms) are given by the square-roots of the diagonal elements in the matrix of inner products. These lengths, are proportional (scaling 2) and equal (scaling 4) to the standard deviations of the original variables.
apply(X, 2, sd)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 6.592230 9.752493 11.698765 5.710614 6.223767 5.391197
sqrt(apply(E, 1, function(x) sum(x^2)))
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 1 1 1 1 1 1
sqrt(apply(E2, 1, function(x) sum(x^2)))
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 18.64564 27.58421 33.08911 16.15206 17.60347 15.24861
sqrt(apply(E3, 1, function(x) sum(x^2)))
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 3.743663 5.142620 5.471886 3.746464 3.308392 3.461031
sqrt(apply(E4, 1, function(x) sum(x^2)))
## POLLA CHEPO ECHCG AMARE XANST POLAV
## 6.592230 9.752493 11.698765 5.710614 6.223767 5.391197This leads us to the third interpretational rule: starting from a column-centered matrix, the lengths of arrows approximate the standard deviations of the original variables only with a correlation biplot (scaling 2) or with a type 4 biplot.. Furthermore, the inner products of two arrows, approximate the codeviances (Scaling 2) and the covariances (Scaling 4).
Rule 5: Angles between arrows
We have seen that the cosines of the angles between the row-vectors in the matrices E to E4 can be calculated by taking, for each pair of rows, the inner product and the respective norms. By using the functione defined above, it is easy to see that the angles between arrows in E and E3 are totally meaningless. Otherwise, the cosines of the angles between row-vectors in E2 and E4 are equal to the correlations between the original variables.
cosAngles(E2)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## POLLA 1.0000000 -0.4714266 0.6309353 0.7499753 0.8235940 0.6152573
## CHEPO -0.4714266 1.0000000 -0.3603326 -0.3768197 -0.4599788 -0.2866398
## ECHCG 0.6309353 -0.3603326 1.0000000 0.3964563 0.8466435 0.6943966
## AMARE 0.7499753 -0.3768197 0.3964563 1.0000000 0.4458008 0.3177744
## XANST 0.8235940 -0.4599788 0.8466435 0.4458008 1.0000000 0.8441605
## POLAV 0.6152573 -0.2866398 0.6943966 0.3177744 0.8441605 1.0000000
cosAngles(E4)
## POLLA CHEPO ECHCG AMARE XANST POLAV
## POLLA 1.0000000 -0.4714266 0.6309353 0.7499753 0.8235940 0.6152573
## CHEPO -0.4714266 1.0000000 -0.3603326 -0.3768197 -0.4599788 -0.2866398
## ECHCG 0.6309353 -0.3603326 1.0000000 0.3964563 0.8466435 0.6943966
## AMARE 0.7499753 -0.3768197 0.3964563 1.0000000 0.4458008 0.3177744
## XANST 0.8235940 -0.4599788 0.8466435 0.4458008 1.0000000 0.8441605
## POLAV 0.6152573 -0.2866398 0.6943966 0.3177744 0.8441605 1.0000000This leads to the fourth interpretational rule: starting from a column-centered matrix, scaling 2 and scaling 4 result in biplots where the cosines of the angles between arrows approximate the correlation of original variables. Consequently, right angles indicate no correlation, acute angles indicate positive correlatione (the smaller the angle the higher the correlation), while obtuse angles (up to 180°) indicate a negative correlation.
Rule 6: Inner products between markers and arrows
We have seen that, by multiplication, the subject-scores and trait-scores return the original centered matrix and this is totally independent from scaling. Accordingly, we can also say that the observed value for each subject in each variable can be obtained by using the inner product of a subject-vector and a trait-vector.
For example, let’s calculate the inner product between the first row in G (subject A) and the first row in E:
crossprod(G[1,], E[1,])
## [,1]
## [1,] -8.033333That is the exact value shown by A on POLLA, in the original centered data matrix.
Therefore, the fifth interpretational rule is that: independent on scaling, we can approximate the value of one subject in one specific variable, by considering how long are the respective trait-arrow and the projection of the subject-marker on the trait-arrow. If the projection is on the same direction of the trait-arrow, the original value is positive (i.e., above the mean), while if the projection is in the opposite direction, the original value is negative (i.e., below the mean).
What if we standardise the original data?
Sometimes we need to standardise our data, for example because we want to avoid that a few of the original variables (the ones with largest values) assume a preminent role in the ordination of subjects. From a practical point of view, this is very simple: we only have to add the option scale = T to the selected R function for PCA.
What does it change, with the interpretation of a biplot? The main thing to remember is that the starting point is a standardised matrix where each value represents the difference with respect to the column mean in standard deviation units. Furthermore, all the original columns, after standardisation, have unit standard deviation. Accordingly, there are some changes to the interpretational rules, which I have listed in the table above.
Conclusions
I’d like to conclude with a couple of take-home messages, to be kept in mind when publishing a biplot. Please, note that they are taken from Onofri et al., (2010):
- Always mention what kind of pre-manipulation has been performed on the original dataset (centering, normalisation, standardisation).
- Always mention what sort of rescaling on PCs has been used. Remember that the selection of one particular scaling option strongly affects the interpretation of the biplot, in terms of distances and angles. For example, one scaling may allow Euclidean distances between objects to be interpreted, but not those between variables, while another scaling does not permit either.
- Never drag and pull a PCA plot so that it fits the page layout. Remember that axes need to be equally scaled for any geometric interpretations of distances and angles.
Thanks for reading!
Prof. Andrea Onofri
Department of Agricultural, Food and Environmental Sciences
University of Perugia (Italy)
Send comments to: andrea.onofri@unipg.it
References
- Borcard, D., Gillet, F., Legendre, P., 2011. Numerical Ecology with R. Springer Science+Business Media, LLC 2011, New York.
- Gower, J.C., 1966. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika 53, 325–338.
- Legendre, P., Legendre, L., 2012. Numerical ecology. Elsevier, Amsterdam (The Netherlands).
- Kroonenberg, P.M., 1995. Introduction to biplots for GxE tables. The University of Queensland. Research Report #51, Brisbane, Australia.
- Onofri, A., Carbonell, E.A., Piepho, H.-P., Mortimer, A.M., Cousens, R.D., 2010. Current statistical issues in Weed Research. Weed Research 50, 5–24.