Capitolo 7 Modelli ANOVA ad una via

Nel capitolo 4 abbiamo già parlato di come assumiamo che risultati di un esperimento si generino attraverso un doppio meccanismo deterministico e stocastico, rappresentabile attraverso un modello matematico contenento uno o più elementi casuali, descritti da una funzione di densità, solitamente gaussiana. Abbiamo già visto che i modelli più utilizzati sono lineari e, tra questi, il gruppo più diffuso, almeno in ambito biologico-agrario, è quello dei modelli ANOVA.

La nomenclatura è impropria; infatti, con il termine ANOVA, si intende un’operazione di scomposizione della varianza, inventata da Fisher negli anni ‘30 del ’900, che costituisce ancora oggi una delle più fondamentali tecniche di analisi dei dati sperimentali. Tuttavia, ci sono alcuni modelli che, più naturalmente di altri, sono connessi all’esecuzione dell’ANOVA fisheriana. Si tratta di modelli lineari nei quali la/le variabile/i indipendenti, che descrivono gli stimoli sperimentali, sono nominali (categoriche) e, nella letteratura anglosassone, prendono il nome di ’factors’ (fattori sperimentali).

Questi modelli rappresentano il punto di ingresso nell’analisi dei dati e la gran parte della letteratura scientifica è basata proprio su questi modelli. Pertanto, ad essi dedicheremo ampio spazio nel seguito di questo libro.

7.1 Caso-studio: confronto tra erbicidi in vaso

Abbiamo eseguito un esperimento in vaso, nel quale abbiamo utilizzato quattro trattamenti erbicidi:

Metribuzin
Rimsulfuron
Metribuzin + rimsulfuron
Testimone non trattato

Lo scopo dell’esperimento era quello di verificare se la miscela metribuzin e rimsulfuron è più efficace dei due componenti utilizzati separatamente. L’esperimento era disegnato a randomizzazione completa con quattro repliche e prevedeva il rilievo della biomassa presente su ogni vaso, tre settimane dopo il trattamento: un più basso valore di biomassa implica un miglior effetto del trattamento.

I risultati di questo esperimento sono riportati nel dataset ‘mixture.csv’, che è disponibile su una repository web. Per prima cosa, carichiamo il file.

fileName <- "https://www.casaonofri.it/_datasets/mixture.csv"
dataset <- read.csv(fileName, header = T)
head(dataset)
##             Treat Weight
## 1 Metribuzin__348  15.20
## 2 Metribuzin__348   4.38
## 3 Metribuzin__348  10.32
## 4 Metribuzin__348   6.80
## 5     Mixture_378   6.14
## 6     Mixture_378   1.95

Il dataset è organizzato come un database, nel quale ogni riga contraddistingue un’unità sperimentale (record) e ogni colonna rappresenta una caratteristica del record (campo). In questo caso abbiamo due colonne: una per la variabile indipendente (fattore sperimentale ‘Treat’), che ci dice con quale erbicida è stata trattata ogni unità sperimentale, ed una per la variabile dipendente (‘Weight’).

7.2 Descrizione del dataset

La prima analisi dei dati consiste nella valutazione descrittiva del dataset. In particolare, calcoliamo:

le medie per ogni tesi sperimentale
Le deviazioni standard per ogni tesi sperimentale

Utilizziamo la funzione tapply in R.

medie <- tapply(dataset$Weight, dataset$Treat, mean)
SDs <- tapply(dataset$Weight, dataset$Treat, sd)
descrit <- cbind(medie, SDs)
descrit
##                   medie      SDs
## Metribuzin__348  9.1750 4.699089
## Mixture_378      5.1275 2.288557
## Rimsulfuron_30  16.8600 4.902353
## Unweeded        26.7725 3.168673

Che cosa ci dice questa tabella, in base agli obiettivi dell’esperimento?

Ci suggerisce che:

La miscela sembra leggermente più efficace dei prodotti singoli
Esiste una certa variabilità (errore sperimentale), che impedisce un giudizio certo
La variabilità è abbastanza simile per tutti i trattamenti

7.3 Definizione di un modello lineare

Sappiamo che, dietro ai campioni osservati, vi sono una o più popolazioni di riferimento, alle quali è rivolto il nostro interesse: abbiamo infatti osservato \(m_1\), \(m_2\), \(m_3\) ed \(m_4\) (le medie dei campioni), ma siamo effettivamente interessati a conoscere \(\mu_1\), \(\mu_2\), \(\mu_3\) e \(\mu_4\), cioè le medie delle popolazioni da cui i campioni sono tratti. E siamo anche interessati a capire se la differenza è sufficientemente ampia da poter ritenere che non sia di natura puramente casuale.

Per descrivere le osservazioni possiamo utilizzare un modello lineare del tipo:

\[Y_i = \mu + \alpha_j + \varepsilon_i\]

Questo modello impone che le osservazioni \(Y\) derivino da una valore \(\mu\), detto intercetta, a cui si aggiunge l’effetto del trattamento \(\alpha_j\) e l’effetto stocastico \(\varepsilon\), che è un elemento che influenza ogni singola osservazione \(i\).

Il valore atteso per un soggetto, in assenza di errore sperimentale, è:

\[\bar{Y_i} = \mu + \alpha_j\]

È abbastanza facile intuire che, se non ci fosse l’errore sperimentale, un soggetto dovrebbe avere un valore pari alla media del gruppo di cui fa parte, per cui:

\[\bar{Y_i} = \mu_j = \mu + \alpha_j\]

7.4 Parametrizzazione del modello

Dobbiamo spendere alcune parole per capire il significato della espressione prima riportata (\(Y_i = \mu + \alpha_j + \varepsilon_i\)) con la quale, di fatto, ci stiamo proponendo di ottenere la quantità \(Y_i\) (ognuno dei dati osservati) come somma di tre valori incogniti. È chiaro che, posto in questi termini, il problema è indeterminato. Infatti esistono infinite triplette di valori che, sommati, possono restituire \(Y_i\), qualunque esso sia. Proviamo per un attimo a considerare il primo dato del nostro dataset, cioè \(15.20\): esso può essere ottenuto come \(10 + 5 + 0.2\) oppure come \(9 + 6 + 0.2\) oppure in un numero infinito di altri modi diversi. Come facciamo allora a individuare i valori \(\mu\), \(\alpha_j\) e \(\varepsilon_i\)? Dobbiamo porre qualche vincolo, in modo che il problema diventi determinato.

Una prima possibilità consiste nell’imporre che la somma degli \(\alpha_j\) sia pari a 0 (vincolo sulla somma). Abbiamo visto che le medie dei quattro gruppi (\(\mu_j\)) sono pari alla somma \(\mu + \alpha_j\) e quindi, sommando le quattro medie otteniamo:

\[ \mu_1 + \mu_2 + \mu_3 + \mu_4 = 4 \mu + \sum{\alpha_j}\]

Con il vincolo sulla somma:

\[ \mu_1 + \mu_2 + \mu_3 + \mu_4 = 4 \mu\]

quindi:

\[\mu = \frac{\mu_1 + \mu_2 + \mu_3 + \mu_4}{4} \]

cioè \(\mu\) è la media generale e \(\alpha_j\) rappresentano gli scostamenti di ogni trattamento rispetto alla media generale, usualmente definiti effetti dei trattamenti. Se un prodotto è efficace, abbasserà di più il peso delle infestanti e quindi avrà un elevato effetto negativo.

Ora il problema è completamente definito: se \(\mu = 14.48375\) e \(\mu_1 = 9.175\) allora deve essere \(\alpha_1 = 9.175 - 14.48375 = -5.30875\) ed \(\epsilon_1 = 15.20 - 9.175 = 6.025\), cosicché \(14.48375 - 5.30875 + 6.025 = 15.20 = Y_1\).

Questa parametrizzazione con vincolo sulla somma è abbastanza ben ‘comprensibile’ e, se il disegno è bilanciato, è facile stimare i parametri ‘a mano’, partendo dalle medie aritmetiche dei trattamenti e dalla media generale, come vedremo tra poco. Tuttavia, non possiamo non precisare che questa parametrizzazione non è quella utilizzata di default dalla gran parte dei software statistici, incluso R. In particolare, R impone il vincolo che \(\alpha_1 = 0\) (vincolo sul trattamento), in modo che:

\[ \left\{ {\begin{array}{l} \mu_1 = \mu + \alpha_1 = \mu + 0\\ \mu_2 = \mu + \alpha_2 \\ \mu_3 = \mu + \alpha_3 \\ \mu_4 = \mu + \alpha_4 \end{array}} \right.\]

Di conseguenza, \(\mu\) è la media del primo trattamento, usualmente inteso in ordine alfabetico (ma il riferimento può cambiare, a seconda delle esigenze) a i valori \(\alpha_j\), sono differenze tra le medie dei gruppi da 2 a 4 con la media del gruppo 1. Anche in questo caso, il problema è completamente definito: la prima osservazione deve essere ottenuta sommando \(\mu = 9.175\) (media del primo trattamento), \(\alpha_1 = 0\) ed un valore \(\epsilon\) che possiamo individuare come pari a \(\epsilon_1 = Y_1 - \mu_1 = 5.20 - 9.175 = 6.025\).

Vediamo che le stima di \(\mu\) ed \(\alpha_j\) ottenute con le due parametrizzazioni sono diverse, ma il residuo \(\epsilon\) non cambia. Nel seguito di questo libro, per i calcoli manuali utilizzeremo sempre il vincolo sulla somma, che è più facile da gestire e dovremo tener presente che le nostre stime non corrisponderanno con quelle ottenute con R con le impostazioni di default. Ma, come vedremo, entrambi i metodi ci porteranno alle stesse conclusioni.

7.5 Assunzioni di base

In questa costruzione algebrica abbiamo implicitamente posto alcuni ‘punti fermi’, detti assunzioni di base, che sono i seguenti:

la componente deterministica è lineare e additiva (\(\mu + \alpha_j\))
non vi sono altri effetti, se non il trattamento e l’errore, che è puramente stocastico, senza componenti sistematiche
gli errori sono campionati in modo indipendente, da una distribuzione normale, con media 0 e deviazione standard \(\sigma\)
le varianze sono omogenee (unico valore di \(\sigma\), comune per tutti i gruppi)

È evidente che il nostro dataset deve conformarsi a queste nostre aspettative, altrimenti il modello è invalido. Ci occuperemo di questa verifica nel prossimo capitolo.

7.6 Fitting del modello: metodo manuale

Abbiamo definito un modello con il quale descrivere le nostre osservazioni sperimentali. Ora bisogna assegnare un valore ai parametri di questo modello, cioè \(\mu\), \(\alpha_1\), \(\alpha_2\), \(\alpha_3\), \(\alpha_4\) e \(\sigma\), in modo che il modello non sia più una rappresentazione generale di un fenomeno, bensì diventi una rappresentazione specifica del nostro esperimento. Anche se nella pratica professionale il model fitting viene eseguito con il computer, inzialmente procederemo a mano, per comprendere bene il senso delle operazioni effettuate. In genere, il model fitting si compone delle seguenti fasi:

stima dei parametri \(\mu\) ed \(\alpha\);
calcolo dei residui;
stima di \(\sigma\)
scomposizione delle varianze;
test d’ipotesi ed inferenza.

7.6.1 Stima dei parametri

Imponendo un vincolo sulla somma e considerando che il disegno è bilanciato (stesso numero di repliche per tutti i trattamenti), la stima dei parametri può essere fatta a mano, a partire dalle medie aritmetiche dei trattamenti e dalla media generale (metodo dei momenti). La media generale è \(14.48375\), quindi:

\[ \left\{ {\begin{array}{l} \mu = 14.48375\\ \alpha_1 = \mu_1 - \mu = 9.175 - 14.48375 = - 5.30875\\ \alpha_2 = \mu_2 - \mu = 5.1275 - 14.48375 = - 9.35625\\ \alpha_3 = \mu_3 - \mu = 16.86 - 14.48375 = 2.37625\\ \alpha_4 = \mu_4 - \mu = 26.7725 - 14.48375 = 12.28875\\ \end{array}} \right.\]

7.6.2 Calcolo dei residui

Abbiamo già visto che i valori attesi (\(\bar{Y_i}\)) sono pari, per ogni osservazione, alla somma tra \(\mu\) e il valor \(\alpha\) relativo al gruppo di cui l’osservazione fa parte. Per facilitare i calcoli, costruiamo una tabella in cui riportiamo la media generale, gli affetti \(\alpha_j\) e i valori attesi, ottenuti come indicato poco fa. I residui possono essere calcolati facilmente, come scostamenti tra i valori osservati e i valori attesi (Tabella 7.1).

Tabella 7.1: Tabella dei dati osservati, dei valori attesi, dei residui e dei loro quadrati
Erbicida	Weight	mu	alpha	Attesi	Residui
Metribuzin__348	15.20	14.484	-5.309	9.175	6.025
Metribuzin__348	4.38	14.484	-5.309	9.175	-4.795
Metribuzin__348	10.32	14.484	-5.309	9.175	1.145
Metribuzin__348	6.80	14.484	-5.309	9.175	-2.375
Mixture_378	6.14	14.484	-9.356	5.127	1.013
Mixture_378	1.95	14.484	-9.356	5.128	-3.178
Mixture_378	7.27	14.484	-9.356	5.127	2.142
Mixture_378	5.15	14.484	-9.356	5.128	0.023
Rimsulfuron_30	10.50	14.484	2.376	16.860	-6.360
Rimsulfuron_30	20.70	14.484	2.376	16.860	3.840
Rimsulfuron_30	20.74	14.484	2.376	16.860	3.880
Rimsulfuron_30	15.50	14.484	2.376	16.860	-1.360
Unweeded	24.62	14.484	12.289	26.773	-2.153
Unweeded	30.94	14.484	12.289	26.773	4.167
Unweeded	24.02	14.484	12.289	26.773	-2.753
Unweeded	27.51	14.484	12.289	26.773	0.737

7.6.3 Stima di \(\sigma\)

Abbiamo detto che \(\sigma\) è la deviazione standard dei residui, che tuttavia deve essere calcolata facendo attenzione al numero dei gradi di libertà. In primo luogo, calcoliamo la devianza dei residui, cioè la somma dei quadrati degli scarti rispetto alla media (RSS: Residual Sum of Squares). Siccome la media dei residui è zero per definizione, la devianza dei residui non è altro che la somma dei loro quadrati ed è pari a:

\[\textrm{RSS} = 6.025^2 + (-4.795^2) ... + 0.738^2 = 184.1774\]

I residui costituiscono lo scostamento di ogni dato rispetto alla media del trattamento e, di conseguenza, per ogni gruppo la loro somma deve essere 0. Quindi per ogni gruppo vi sono 3 gradi di libertà, cioè 12 gradi di libertà in totale (3 \(\times\) 4, cioè il numero dei trattamenti per il numero delle repliche meno una). Ne consegue che la varianza dei residui è pari a:

\[MS_{e} = \frac{184.178}{12} = 15.348\]

La deviazione standard \(\sigma\) è:

\[ \sqrt{15.348} = 3.9177\]

7.7 Scomposizione della varianza

La scomposizione della varianza, il cui significato sarà più chiaro in seguito, è la vera e propria ANOVA fisheriana, che può essere eseguita facilmente utilizzando la Tabella 7.1.

Il primo elemento da stimare è la devianza totale dei dati, cioè la somma dei quadrati degli scarti di ogni dato rispetto alla media generale:

\[\begin{array}{c} SS = \left(24.62 - 14.48375\right)^2 + \left(30.94 - 14.48375\right)^2 + ... \\ ... + \left(15.50 - 14.48375\right)^2 = 1273.706 \end{array}\]

Questa devianza esprime la variabilità totale tra un dato e l’altro, sia quella dovuta al trattamento, sia quella puramente stocastica.

Abbiamo già calcolato la devianza dei residui (RSS = 184.17745), che quantifica la variabilità dei dati dovuta ad effetti puramente casuali, ma non al trattamento sperimentale. Infatti, la variabilità di un dato rispetto alla media del gruppo a cui appartiene non può essere dovuta al trattamento, in quanto i soggetti dello stesso gruppo sono trattati allo stesso modo.

A questo punto ci chiediamo: qual è la devianza prodotta dal trattamento sperimentale? La devianza totale rappresenta la variabilità totale dei dati (trattamento + effetti stocastici), la devianza residua rappresenta la sola variabilità stocastica, di conseguenza, la differenza di queste due quantità rappresenta la devianza dovuta al trattamento sperimentale:

\[SS_t = SS - RSS = 1273.706 + 184.1774 = 1089.529\]

In realtà, oltreché per differenza, la devianza del trattamento potrebbe anche essere ottenuta direttamente, sommando i quadrati dei valori \(\alpha\), il che equivale al quadruplo (abbiamo quattro repliche) della devianza tra le medie dei trattamenti:

\[{\begin{array}{l} SS_t = 4 \times \left[ \left(9.1750 - 14.48375\right)^2 + \left(5.1275 - 14.48375\right)^2 + \right. \\ + \left. \left(16.86 - 14.48375\right)^2 + \left(26.7725 - 14.48375\right)^2 \right] = 1089.529 \end{array}}\]

A questo punto, ricordiamo che il nostro obiettivo è stabilire se il trattamento ha avuto un effetto significativo, cioè se l’effetto da esso prodotto si distingue dal ‘rumore di fondo’, ossia dall’elemento casuale rappresentato dal residuo. Tuttavia, le devianza del trattamento e del residuo non possono essere confrontate direttamente, in quanto hanno un numero diverso di gradi di libertà.

In particolare, la devianza del trattamento ha tre gradi di libertà (tre scarti liberi; in genere numero dei trattamenti - 1) e quindi la relativa varianza è:

\[MS_t = \frac{1089.529}{3} = 363.1762\]

La varianza del residuo è invece pari a 15.348 e, come abbiamo visto più sopra, ha 12 gradi di libertà. Le due varianze così ottenute possono essere confrontate, all’interno di una procedura di test d’ipotesi, che vedremo di seguito.

Prima, però, vale la pena di sottolineare come la procedura precedente ci abbia permesso di suddividere la variabilità totale delle osservazioni in due componenti, una dovuta al trattamento e una dovuta all’errore sperimentale. Per questo motivo, parliamo di scomposizione della varianza (variance partitioning) o analisi della varianza (ANalysis Of VAriance = ANOVA), che è lo strumento più utilizzato nella sperimentazione biologica e che dobbiamo totalmente all’inventiva di Ronald Fisher.

7.8 Test d’ipotesi

Abbiamo descritto il nostro esperimento e ne abbiamo individuato le caratteristiche rilevanti, stimando i parametri che meglio le descrivono (effetti dei trattamenti e varianza). Come già detto, dobbiamo chiederci se i dati rispettano le assunzioni di base del modello, ma di questo parleremo in una lezione a parte.

Ora, il nostro scopo è capire se il trattamento sperimentale abbia prodotto un effetto rilevante, maggiore di quello prodotto da altri elementi puramente casuali (‘rumore di fondo’).

L’ipotesi nulla è che il trattamento non abbia avuto effetto, cioè che:

\[H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4\]

In altri termini, se l’ipotesi nulla è vera, i quattro campioni sono estratti da quattro popolazioni identiche, o meglio, dalla stessa popolazione. Ciò può essere anche declinato come:

\[H_0: \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4 = 0\]

Una statistica rilevante per testare questa ipotesi è data dal rapporto tra la varianza del trattamento e quella dell’errore:

\[F = \frac{MS_t}{MS_e} = \frac{363.18}{15.348} = 23.663\]

E’ evidente che se il trattamento non fosse stato efficace, non dovrebbe aver prodotto una variabilità di molto superiore a quella dell’errore (quindi F = 1). In questo caso la variabilità prodotta dal trattamento è stata oltre 23 volte superiore a quella dell’errore. Delle due l’una: o il trattamento è stato efficace oppure io sono stato particolarmente sfortunato e, nell’organizzare questo esperimento, si è verificato un caso particolarmente raro.

Ci chiediamo: “se l’ipotesi nulla è vera, qual è la probabilità di osservare un valore di F così alto o più alto?”. In altre parole, “qual è la sampling distribution per F?”. Potremmo costruire questa distribuzione empiricamente, attraverso una simulazione Monte Carlo.

Se assumiamo che l’ipotesi nulla è vera, allora i dati dovrebbero essere campionati da una distribuzione gaussiana con media pari a 14.48375 e deviazione standard pari a 3.9177 (vedi sopra). In base a questo, possiamo utilizzare un generatore di numeri casuali gaussiani, per ottenere un dataset, per il quale l’ipotesi nulla è certamente vera, perché non vi è l’effetto del trattamento, come mostriamo nel box sottostante:

Ysim <- rnorm(16, 14.48375, 3.9177)
Ysim
##  [1] 11.25108 15.84385 10.87910 13.35805 12.32459 17.80849 19.59052
##  [8] 12.41272 17.47276 21.49765 16.50393 16.48161 17.92167 13.28823
## [15] 10.57145 17.53845

Se sottoponiamo questo dataset alla scomposizione della varianza, possiamo calcolare il relativo valore F. Se ripetiamo questo processo, ad esempio, 100’000 volte, otteniamo 100’000 valori F compatibili con l’ipotesi nulla, in quanto generati assumendola come vera. Otteniamo quindi una sampling distribution empirica per F e possiamo valutare qual è la probabilità di ottenere valori superiori a 23.66. In questo caso, il test è ad una sola coda, perché la statistica F è un rapporto do varianze, che sono, per definizione, positive.

Per chi voglia eseguire questa simulazione, il codice da utilizzare è riportato nel box sottostante.

# Fvals <- c()
# set.seed(1234)
# for(i in 1:100000){
#   Ysim <- rnorm(16, 14.48375, 3.9177)
#   mu <- mean(Ysim)
#   muj <- rep(tapply(Ysim, dataset$Treat, mean), each = 4)
#   alpha <- muj - mu
#   epsilon <- Ysim - (mu + alpha)
#   Fvals[i] <- (sum(alpha^2)/3)/(sum(epsilon^2)/12)
# }
# min(Fvals)
# max(Fvals)
# length(Fvals[Fvals > 23.663])
# min(Fvals)
# [1] 0.0001855014
# max(Fvals)
# [1] 32.87431
# mean(Fvals)
# [1] 1.194453
# median(Fvals)
# [1] 0.8362404
# length(Fvals[Fvals > 23.663])
# [1] 2

Il valore minimo di F è stato 0.00019, il massimo 32.87, la media è stata 1.19 e la mediana 0.84. Tra tutti i 100’000 valori, ne abbiamo trovati solo due pari o superiori a quello osservato, il che vuol dire che la probabilità che l’ipotesi nulla sia vera con F = 23.66 è pari a 2 \(\times 10^{-5}\).

La sampling distribution (opportunamente discretizzata) è riportata in figura 7.1. Si tratta di una distribuzione chiaramente non normale, ma descrivibile con la funzione di densità F di Fisher (in realtà l’invenzione è di Snedecor, allievo di Fisher), con 3 gradi di libertà al numeratore e 12 al denominatore (in blue in figura).

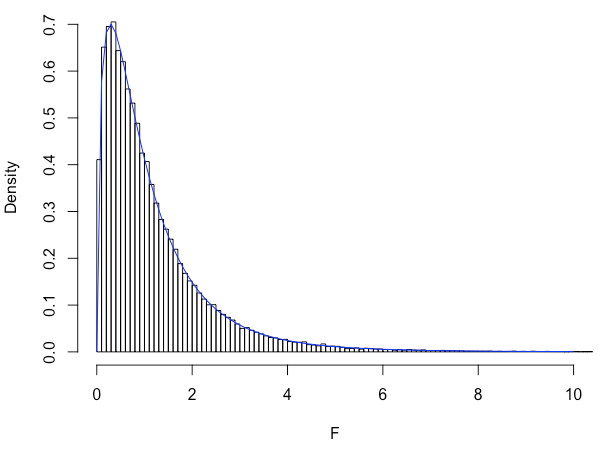
Sampling distribution empirica per la statistica F, ottenuta assumendo vera l'ipotesi nulla. La linea azzurra rappresenta la funzione di densità F di Fisher, con 3 e 12 gradi di libertà.

Figura 7.1: Sampling distribution empirica per la statistica F, ottenuta assumendo vera l’ipotesi nulla. La linea azzurra rappresenta la funzione di densità F di Fisher, con 3 e 12 gradi di libertà.

Di conseguenza, possiamo evitare la simulazione Monte Carlo ed utilizzare la F di Fisher per calcolare la probabilità di ottenere un valore di F altrettanto estremo o più estremo del nostro. Ad esempio, in R, possiamo utilizzare la funzione:

pf(23.663, 3, 12, lower.tail = F)
## [1] 2.508789e-05

che porta ad un risultato molto simile a quello ottenuto con la simulazione di Monte Carlo. Insomma, in assenza di un effetto del trattamento (quindi per il solo effetto del caso), se ripetessimo l’esperimento infinite volte, avremmo una probabilità molto bassa che si produca un valore di F altrettanto alto o più alto di quello da noi osservato.

Di conseguenza, rifiutiamo l’ipotesi nulla di assenza di effetto del trattamento e accettiamo l’ipotesi alternativa (il trattamento ha avuto effetto significativo). In questo modo, ci assumiamo un rischio d’errore estremamente piccolo, comunque molto al disotto della soglia prefissata del 5%.

7.9 Inferenza statistica

Abbiamo visto che la varianza d’errore è pari a 15.348 e pertiene ad ogni singola osservazione effettuata durante l’esperimento. Questa osservazione ci può aiutare a costruire una banda di inferenza attorno alle medie stimate; infatti, noi abbiamo osservato \(m_1\), \(m_2\), \(m_3\) ed \(m_4\) e con la nostra stima puntuale, abbiamo assunto che i valori osservati coincidessero rispettivamente con \(\mu_1\), \(\mu_2\), \(\mu_3\) e \(\mu_4\). Analogamente a quanto abbiamo visto in un capitolo precedente, possiamo calcolare l’incertezza associata alle nostre stime attraverso l’Errore Standard di una Media (SEM), pari a:

\[SEM = \sqrt{ \frac{MS_e}{n} } = \frac{3.9177}{\sqrt{4}}\]

Oltre che di una media, spesso siamo interessati anche a conoscere la varianza della differenza di due medie. Dato che la differenza di variabili casuali ha una varianza pari alla somma delle varianza delle due variabili originali, possiamo scrivere che:

\[SED = \sqrt{ MS_{media1} + MS_{media2} } = \sqrt{ 2 \cdot \frac{MS_e}{n} } = \sqrt{2} \cdot \frac{3.9177}{\sqrt{4}} = \sqrt{2} \cdot SEM\]

7.10 Fitting del modello con R

La stima dei parametri di un modello lineare, in R, può essere eseguita in modo molto banale, utilizzando la funzione ‘lm()’ Il codice è il seguente:

mod <- lm(Weight ~ factor(Treat), data = dataset)

Il primo argomento rappresenta il modello lineare che vogliamo adattare ai dati: l’incusione dell’intercetta, codificata con il carattere ‘1’ è opzionale (‘Weight ~ 1 + Treat’ e ‘Weight ~ Treat’ sono equivalenti), mentre il termine stocastico \(\epsilon\) viene incluso di default e non deve essere indicato. Il termine ‘factor’ sta a significare che la variabile ‘Treat’ è un fattore sperimentale; questa specifica è opzionale quando la variabile è di tipo ‘carattere’ (come in questo caso), ma è fondamentale quando abbiamo a che fare con una variabile a codifica numerica.

Una volta operato l’adattamento, l’oggetto ‘mod’ contiene tutti i risultati, che possiamo ottenere con opportuni ‘estrattori’. Ad esempio, la funzione ‘summary()’ restituisce le stime dei parametri:

summary(mod)
## 
## Call:
## lm(formula = Weight ~ factor(Treat), data = dataset)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -6.360 -2.469  0.380  2.567  6.025 
## 
## Coefficients:
##                             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                    9.175      1.959   4.684 0.000529 ***
## factor(Treat)Mixture_378      -4.047      2.770  -1.461 0.169679    
## factor(Treat)Rimsulfuron_30    7.685      2.770   2.774 0.016832 *  
## factor(Treat)Unweeded         17.598      2.770   6.352 3.65e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.918 on 12 degrees of freedom
## Multiple R-squared:  0.8554, Adjusted R-squared:  0.8193 
## F-statistic: 23.66 on 3 and 12 DF,  p-value: 2.509e-05

Notiamo immediatamente che viene utilizzata la parametrizzazione con vincolo sul trattamento, visto che l’intercetta coincide con la media del primo trattamento. I valori di \(\alpha\) non sono altro che differenze tra questa media e tutte le altre medie.

I valori attesi e i residui possono essere ottenuti, in R, applicando due metodi ‘fitted()’ e ‘residuals()’ all’oggetto ottenuto dal fitting:

attesi <- fitted(mod)
epsilon <- residuals(mod)

La devianza del residuo (somma dei quadrati degli scarti) è:

deviance(mod)
## [1] 184.1774

ementre la deviazione standard del residuo (\(\sigma\)), già visualizzabile nell’output della funzione ‘summary()’, può essere estratta come:

summary(mod)$sigma
## [1] 3.917668

La tabella finale dell’ANOVA può essere ottenuta in R utilizzando la seguente funzione:

anova(mod)
## Analysis of Variance Table
## 
## Response: Weight
##               Df  Sum Sq Mean Sq F value    Pr(>F)    
## factor(Treat)  3 1089.53  363.18  23.663 2.509e-05 ***
## Residuals     12  184.18   15.35                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

7.11 Medie marginali attese

Abbiamo visto che le somme \(\mu + \alpha_j\) restituiscono le medie dei trattamenti e prendono il nome di medie marginali attese. Quando l’esperimento è bilanciato (ugual numero di repliche per ogni trattamento), esse sono uguali alle medie aritmetiche di ogni gruppo, mentre, quando l’esperimento è sbilanciato esso sono diverse, ma costituiscono una stima migliore delle medie delle popolazioni da cui i gruppi sono estratti rispetto alle medie aritmetiche. In R, il metodo più semplice per calcolare le medie marginali attese è quello di utilizzare la funzione ‘emmeans()’, nel package ‘emmeans’ (Lenth, 2016), che deve essere preventivamente installato e caricato in memoria.

#install.packages("emmeans") # Installare il package
library(emmeans) #Caricare il package in memoria
medie <- emmeans(mod, ~Treat)
medie
##  Treat           emmean   SE df lower.CL upper.CL
##  Metribuzin__348   9.18 1.96 12     4.91     13.4
##  Mixture_378       5.13 1.96 12     0.86      9.4
##  Rimsulfuron_30   16.86 1.96 12    12.59     21.1
##  Unweeded         26.77 1.96 12    22.50     31.0
## 
## Confidence level used: 0.95

7.12 Per concludere …

Con l’ANOVA la variabilità totale dei dati viene decomposta in due quote, una attribuibile al trattamento sperimentale ed una inspiegabile (residuo)
L’effetto del trattamento è significativo, se la variabilità che esso provoca è superiore a quella inspiegabile
Il confronto tra varianze viene impostato sotto forma di rapporto (F).
L’ipotesi nulla è che il trattamento NON HA AVUTO effetto significativo
Sotto questa ipotesi nulla, l’F osservato ha una distribuzione F di Fisher
L’ipotesi nulla è rifiutata quando P \(\leq\) 0.05 (livello di protezione arbitrario, ma universalmente accettato)

Ovviamente, è necessario ricordare che tutte le considerazioni fatte finora sono valide se il dataset è conforme alle assunzioni di base per l’ANOVA, per cui bisogna sempre eseguire i necessari controlli, di cui parleremo nel prossimo capitolo.

7.13 Altre letture

Faraway, J.J., 2002. Practical regression and Anova using R. http://cran.r-project.org/doc/contrib/Faraway-PRA.pdf, R.
Fisher, Ronald (1918). “Studies in Crop Variation. I. An examination of the yield of dressed grain from Broadbalk” (PDF). Journal of Agricultural Science. 11 (2): 107–135.
Kuehl, R. O., 2000. Design of experiments: statistical principles of research design and analysis. Duxbury Press (CHAPTER 2)
Lenth, R.V., 2016. Least-Squares Means: The R Package lsmeans. Journal of Statistical Software 69. https://doi.org/10.18637/jss.v069.i01