Capitolo 12 Modelli ANOVA a due vie con interazione
12.1 Il concetto di ’interazione’
In alcuni casi siamo interessati a valutare l’effetto combinato di due fattori sperimentali, ad esempio, la lavorazione del terreno ed il diserbo chimico, in modo da mettere in evidenza possibili “interazioni”. Con questo termine, intendiamo il fenomeno per cui l’effetto di un fattore (ad es. la lavorazione) cambia a seconda del livello dell’altro fattore (il diserbo chimico).
Per comprendere meglio il concetto, osserviamo la Figura 12.1, dove sono mostrate le medie di quattro trattamenti, ottenuti dalla combinazione fattoriale di un trattamento A con due livelli (A1 e A2) e di un trattamento B con altrettanti livelli (B1 e B2). Nel grafico, ogni combinazione è rappresentata da un simbolo.
Concentriamoci un attimo sul grafico di sinistra e consideriamo la prima combinazione in ordine alfabetico (A1B1): per questa, la media è pari a 10. Se passiamo da A1 ad A2, fermo restando B1, l’incremento è + 4. Se invece passiamo da B1 a B2, fermo restando A1, l’incremento è + 5. Si deduce che, se gli effetti fossero puramente additivi, la media di A2B2 dovrebbe essere pari a 10 + 4 + 5 = 19, in quanto vengono modificati entrambi i livelli, da A1 ad A2 e da B1 a B2. Vediamo che l’osservazione conferma questa aspettativa di additività degli effetti e di mancanza di interazione.
Al contrario, nel grafico centrale vediamo che il risultato osservato di A2B2 non può essere ottenuto per semplice somma di effetti, perché, a fronte di un risultato atteso pari a 19 otteniamo invece 16. Evidentemente, vi è qualcosa in questa combinazione che altera l’effetto congiunto di A e B. Questo qualcosa può essere quantificato con il valore -3, così che la media A2B2 è pari a 10 + 4 + 5 - 3 = 16. Il valore -3 rappresenta la mancanza di additività o interazione; in questo caso si tratta di interazione semplice, in quanto la graduatoria dei trattamenti non cambia: A2 è sempre meglio di A1 e B2 è sempre meglio di B1, anche se gli effetti non sono quelli previsti.
Nel grafico di sinistra la situazione è analoga, ma più estrema: l’effetto dell’interazione è -10 e comporta un’inversione della graduatoria, per cui parliamo di interazione cross-over.
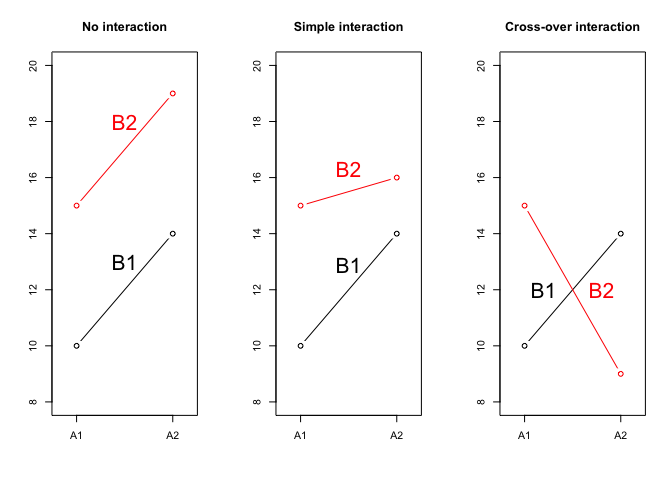
Figura 12.1: Esempi di interazione tra fattori sperimentali
Perchè siamo così interessati all’interazione e, in particolare, all’interazione cross-over? Esaminiamo più da vicino i valori nel grafico a destra in Figura 12.1, riportandoli nella tabella 12.1, insieme alle medie dei quattro livelli A1, A2, B1 e B2. Le medie delle combinazioni sono dette medie di cella, mentre le medie dei livelli principali sono dette medie marginali, perché si trovano al margine della tabella.
| B1 | B2 | Media | |
|---|---|---|---|
| A1 | 10.0 | 15.0 | 12.0 |
| A2 | 14.0 | 9.0 | 12.0 |
| Media | 12.5 | 11.5 | 12.0 |
Se guardassimo solo le medie marginali, avremmo l’impressione sbagliata che il fattore A, da solo, non ha alcun effetto (le medie A1 e A2 sono uguali) e che il fattore B ha solo un piccolissimo effetto. La realtà è invece che entrambi i fattori hanno un grande effetto, ma la presenza dell’interazione lo nasconde completamente, impedendoci di raggiungere conclusioni attendibili guardando ai due fattori, uno separatamente dall’altro.
12.2 Effetti incrociati: interazione tra lavorazioni e diserbo chimico
Un ricercatore ha organizzato un esperimento fattoriale a blocchi randomizzati, dove ha valutato l’effetto di tre tipi di lavorazione del terreno (lavorazione minima = MIN; aratura superficiale = SP; aratura profonda = DP) e di due tipi di diserbo chimico (a pieno campo = TOT; localizzato sulla fila della coltura = PART). L’ipotesi scientifica è che, in caso di diserbo localizzato, il rovesciamento del terreno prodotto dall’aratura sia fondamentale, in quanto sotterra i semi prodotti dalle piante infestanti, impedendone l’emergenza nella coltura successiva.
L’esperimento è completamente incrociato ed include, in totale, sei tratatmenti (tutte e sei le possibili combinazioni tra i due fattori sperimentali) e quattro repliche per un totale di 24 parcelle. Come consuetudine in pieno campo, l’esperimento è organizzato a blocchi randomizzati e le sei tesi sperimentali sono allocate a caso all’interno di ciascun blocco.
I risultati ottenuti con questo esperimento sono disponibili nel file ‘beet.csv’, che si trova nella solita repository online. Col codice sottostante possiamo caricare il file e trasformare tutte le variabili indipendenti in ‘factors’.
fileName <- "https://www.casaonofri.it/_datasets/beet.csv"
dataset <- read.csv(fileName, header=T)
dataset$Tillage <- as.factor(dataset$Tillage)
dataset$WeedControl <- as.factor(dataset$WeedControl)
dataset$Block <- as.factor(dataset$Block)
head(dataset)
## Tillage WeedControl Block Yield
## 1 MIN TOT 1 11.614
## 2 MIN TOT 2 9.283
## 3 MIN TOT 3 7.019
## 4 MIN TOT 4 8.015
## 5 MIN PART 1 5.117
## 6 MIN PART 2 4.30612.3 Definizione del modello lineare
I risultati di questo esperimento sono determinati da quattro elementi:
- l’effetto del blocco
- l’effetto della lavorazione
- l’effetto del diserbo chimico
- l’interazione ‘lavorazione \(\times\) diserbo’
Un modello lineare con questi quattro effetti potrebbe essere scritto:
\[Y_{ijk} = \mu + \gamma_k + \alpha_i + \beta_j + \alpha\beta_{ij} + \varepsilon_{ijk}\] dove \(\gamma\) è l’effetto del blocco \(k\), \(\alpha\) è l’effetto della lavorazione \(i\), \(\beta\) è l’effetto del diserbo \(j\), \(\alpha\beta\) è l’effetto dell’interazione per la specifica combinazione della lavorazione \(i\) e del diserbo \(j\). Oltre a questi elementi ‘deterministici’, i risultati sono influenzati dall’elemento stocastico \(\varepsilon\), associato ad ogni osservazione, che si assume normalmente distribuito con media 0 e deviazione standard pari a \(\sigma\).
12.4 Calcoli manuali
Per completezza d’informazione, illustriamo i calcoli necessari per la scomposizione ‘manuale’ della varianza. Il punto di partenza, come al solito, sono le medie per i livelli di ogni fattore sperimentale e per le loro combinazioni, che calcoliamo con l’usuale funzione tapply().
medieComb <- with(dataset, tapply(Yield,
list(WeedControl, Tillage),
mean))
medieComb
## DP MIN SP
## PART 10.62875 5.99500 8.47525
## TOT 9.20675 8.98275 9.14125
medieLav <- with(dataset, tapply(Yield, Tillage,
mean))
medieLav
## DP MIN SP
## 9.917750 7.488875 8.808250
medieWC <- with(dataset, tapply(Yield, WeedControl,
mean))
medieWC
## PART TOT
## 8.366333 9.110250
medieB <- with(dataset, tapply(Yield, Block,
mean))
medieB
## 1 2 3 4
## 9.385500 8.347500 8.557833 8.662333La media generale è:
Per calcolare gli effetti principali (blocchi, lavorazioni e diserbi), sottraiamo da ogni media la media generale:
gamma <- medieB - mu
alpha <- medieLav - mu
beta <- medieWC - mu
gamma; alpha; beta
## 1 2 3 4
## 0.64720833 -0.39079167 -0.18045833 -0.07595833
## DP MIN SP
## 1.17945833 -1.24941667 0.06995833
## PART TOT
## -0.3719583 0.3719583Per l’interazione, dobbiamo considerare che la media di ogni combinazione è pari a:
\[ \mu_{ij.} = \mu + \alpha_i + \beta_j + \alpha\beta_{ij}\]
e quindi:
\[ \alpha\beta_{ij} = \mu_{ij.} - \mu - \alpha_i - \beta_j\]
Ora, siccome
\[\alpha_i = \mu_{i..} - \mu\]
e
\[\beta_j = \mu_{.j.} - \mu\]
possiamo scrivere:
\[ \alpha\beta_{ij} = \mu_{ij.} - \mu - \mu_{i..} + \mu - \mu_{.j.} + \mu = \mu_{ij.} - \mu_{i..} - \mu_{.j.} + \mu\]
Ad esempio:
\[ \alpha\beta_{sp,part} = 5.995 - 7.488875 - 8.366333 + 8.738292 = - 1.121916\] Completando i calcoli, gli effetti dell’interazione sono pari a:
alphaBeta <- medieComb - rbind(medieLav, medieLav) -
cbind(medieWC, medieWC, medieWC) + mu
alphaBeta
## DP MIN SP
## PART 1.082958 -1.121917 0.03895833
## TOT -1.082958 1.121917 -0.03895833A questo punto possiamo calcolare i valori attesi e i residui, come scostamenti tra valori osservati e valori attesi, anche se questa parte ve la lasciamo per esercizio.
12.4.1 Scomposizione della varianza
Come abbiamo visto nei capitoli precedenti, le devianze di blocchi, lavorazioni e diserbo si calcolano come somme dei quadrati degli effetti, tenendo conto del numero di osservazioni per ogni blocco/lavorazione/diserbo. Ad esempio, in un blocco, abbiamo 6 osservazioni e quindi ognuno dei quattro effetti è ripetuto per sei volte; di conseguenza, la devianza dei blocchi è:
Le altre devianze si calcolano allo stesso modo:
SStil <- 8 * sum(alpha^2)
SStil
## [1] 23.65647
SSwc <- 12 * sum(beta^2)
SSwc
## [1] 3.320472
SScomb <- 4 * sum(alphaBeta^2)
SScomb
## [1] 19.46411Questi calcoli manuali possono essere utili per meglio comprendere il senso della scomposizione della varianza, ma sono da considerare obsoleti, in quanto, nell’uso comune, nessuno li esegue più senza l’aiuto di un computer.
12.5 Calcoli con R
12.5.1 Model fitting
Nella pratica quotidiana, per la stima dei parametri ci affidiamo ad R e al metodo dei minimi quadrati. La definizione del modello è:
Yield ~ Block + Tillage + WeedControl + Tillage:WeedControle può essere abbreviata utilizzando l’operatore ’*’:
Yield ~ Block + Tillage * WeedControlL’intero codice è mostrato nel box sottostante:
12.5.2 Verifica delle assunzioni di base
Prima di procedere, dobbiamo verificare il rispetto delle assunzioni di base, attraverso l’analisi grafica dei residui, come indicato in un capitolo precedente. Il grafico dei residui contro i valori attesi ed il QQ-plot sono riportati in Figura 12.2.
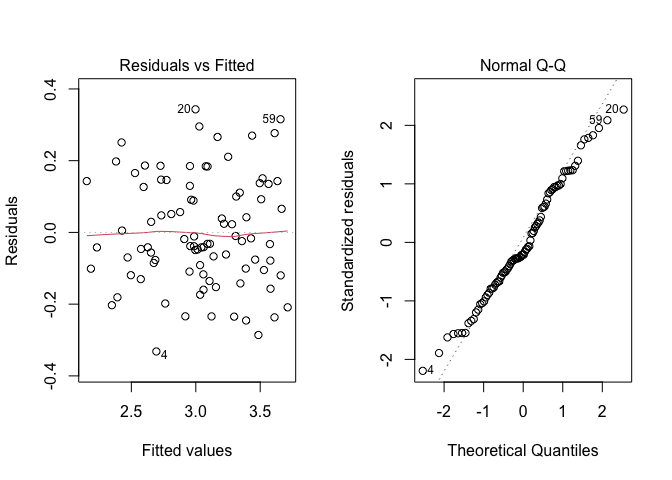
Figura 12.2: Analisi grafica dei residui con R
Il grafico dei residui mostra un sospetto outlier (il settimo dato). Tuttavia, non abbiamo memoria di errori durante la sperimentazione e a parte questo outlier, non paiono esserci problemi di omogeneità delle varianze. Pertanto, decidiamo di ignorare questo potenziale dato aberrante e proseguire nell’analisi, in quanto non sussistono particolare elementi che facciano sospettare qualche patologia dei dati più o meno rilevante.
12.5.3 Scomposizione della varianza
Sfruttando le funzionalità di R e, in particolare, la funzione anova(), otteniamo il seguente risultato:
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## Block 3 3.6596 1.2199 0.6521 0.59389
## Tillage 2 23.6565 11.8282 6.3228 0.01020 *
## WeedControl 1 3.3205 3.3205 1.7750 0.20266
## Tillage:WeedControl 2 19.4641 9.7321 5.2023 0.01922 *
## Residuals 15 28.0609 1.8707
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Come abbiamo visto nei capitoli precedenti, i gradi di libertà degli effetti principali sono pari al numero dei livelli di ogni trattamento meno uno; per quanto riguarda l’interazione, il numero dei gradi di libertà è pari al prodotto dei gradi di libertà degli effetti principali interessati dalla combinazione. In questo caso, l’interazione ‘lavorazione x diserbo’ ha \(2 \times 1 = 2\) gradi di libertà. I gradi di libertà dei residui si ottengono invece per differenza tra i gradi di libertà totali (per 24 dati abbiamo 23 gradi libertà) e i gradi di libertà di tutti gli altri effetti in gioco.
Nel leggere una tabella ANOVA a due (o più) vie, è fondamentale procedere dal basso verso l’alto, guardando subito se l’interazione sia significativa. Se fosse così, dovremmo considerare solo le medie per le combinazioni degli effetti in studio (medie di cella), trascurando invece le medie degli effetti principali (medie marginali), che potrebbero portare a una cattiva interpretazione dei risultati, come abbiamo visto all’inizio di questo capitolo. Se invece l’interazione fosse non significativa, allora potremmo considerare separatamente le medie marginali dei due fattori sperimentali, cosa che potrebbe semplificare notevolmente l’interpretazione.
12.5.4 Medie marginali attese e confronti multipli con R
In questo caso, l’interazione è significativa e, di conseguenza, dobbiamo determinare e confrontare le medie delle sei combinazioni tra lavorazioni e diserbi. In R, possiamo utilizzare la funzione ‘emmeans()’, come abbiamo fatto nei capitoli precedenti. Il codice sottostante permette di calcolare le medie per le combinazioni ‘lavorazione x diserbo’ e confrontare i diserbi a parità di lavorazione (notare l’operatore ‘|’).
library(emmeans)
medie <- emmeans(mod, ~WeedControl|Tillage)
multcomp::cld(medie, Letters = LETTERS)
## Tillage = DP:
## WeedControl emmean SE df lower.CL upper.CL .group
## TOT 9.21 0.684 15 7.75 10.66 A
## PART 10.63 0.684 15 9.17 12.09 A
##
## Tillage = MIN:
## WeedControl emmean SE df lower.CL upper.CL .group
## PART 6.00 0.684 15 4.54 7.45 A
## TOT 8.98 0.684 15 7.53 10.44 B
##
## Tillage = SP:
## WeedControl emmean SE df lower.CL upper.CL .group
## PART 8.48 0.684 15 7.02 9.93 A
## TOT 9.14 0.684 15 7.68 10.60 A
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.Se volessimo confrontare le lavorazioni a parità di diserbo o tutte le combinazioni dovremmo utilizzare una sintassi leggermente diversa:
medie <- emmeans(mod, ~Tillage|WeedControl)
multcomp::cld(medie, Letters=LETTERS)
## WeedControl = PART:
## Tillage emmean SE df lower.CL upper.CL .group
## MIN 6.00 0.684 15 4.54 7.45 A
## SP 8.48 0.684 15 7.02 9.93 AB
## DP 10.63 0.684 15 9.17 12.09 B
##
## WeedControl = TOT:
## Tillage emmean SE df lower.CL upper.CL .group
## MIN 8.98 0.684 15 7.53 10.44 A
## SP 9.14 0.684 15 7.68 10.60 A
## DP 9.21 0.684 15 7.75 10.66 A
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 3 estimates
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.
medie <- emmeans(mod, ~Tillage:WeedControl)
multcomp::cld(medie, Letters=LETTERS)
## Tillage WeedControl emmean SE df lower.CL upper.CL .group
## MIN PART 6.00 0.684 15 4.54 7.45 A
## SP PART 8.48 0.684 15 7.02 9.93 AB
## MIN TOT 8.98 0.684 15 7.53 10.44 AB
## SP TOT 9.14 0.684 15 7.68 10.60 B
## DP TOT 9.21 0.684 15 7.75 10.66 B
## DP PART 10.63 0.684 15 9.17 12.09 B
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## P value adjustment: tukey method for comparing a family of 6 estimates
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.Le tre analisi (contronti tra lavorazioni a parità di diserbo, tra diserbi a parità di lavorazione e tutti verso tutti) portano a risultati leggermente diversi per il diverso numero di confronti effettuati: tre nel primo caso, sei nel secondo e 15 nel terzo, che richiedono una diversa correzione per la molteplicità.
Per completezza di informazioni mostriamo anche il codice necessario per calcolare le medie marginali per le lavorazioni e per il diserbo, anche se non eseguiamo il confronto multiplo, per il motivo indicato in precedenza.
emmeans(mod, ~Tillage)
## Tillage emmean SE df lower.CL upper.CL
## DP 9.92 0.484 15 8.89 10.95
## MIN 7.49 0.484 15 6.46 8.52
## SP 8.81 0.484 15 7.78 9.84
##
## Results are averaged over the levels of: Block, WeedControl
## Confidence level used: 0.95
emmeans(mod, ~WeedControl)
## WeedControl emmean SE df lower.CL upper.CL
## PART 8.37 0.395 15 7.52 9.21
## TOT 9.11 0.395 15 8.27 9.95
##
## Results are averaged over the levels of: Block, Tillage
## Confidence level used: 0.95Ci soffermiamo un attimo sugli errori standard delle medie, che sono diversi per lavorazioni, i diserbi o le loro combinazioni. Infatti, nonostante la varianza dei residui sia la stessa, il numero di dati che concorrono a formare una medie è diverso. Più precisamente, le medie di ogni combinazione ‘diserbo x lavorazione’ hanno quattro repliche, mentre le medie delle lavorazioni hanno otto repliche, cioè quattro per il numero dei diserbi. Analogamente, Le medie dei diserbi hanno dodici repliche, cioè quattro per il numero delle lavorazioni.
Le formula per il calcolo degli errori standard sono le seguenti:
\[SEM_A = \sqrt{\frac{1.87}{4 \cdot 2}} = 0.483\]
\[SEM_B = \sqrt{\frac{1.87}{4 \cdot 3}} = 0.395\]
\[SEM_{AB} = \sqrt{\frac{1.87}{4}} = 0.684\]
Possiamo notare che le medie degli effetti principali, grazie al numero di repliche più elevato, sono stimate con maggiore precisione rispetto alle medie delle combinazioni.
12.6 Effetti innestati: valutazione di ibridi di mais
L’esempio precedente era relativo ad un disegno fattoriale completamente incrociato, dato che i livelli delle lavorazioni erano gli stessi per ogni livello di diserbo. In alcuni casi possiamo trovare disegni innestati, dove i livelli di un fattore cambiano al cambiare dei livelli dell’altro fattore. Nell’esempio seguente abbiamo considerato tre linee pure impollinanti di mais (A1, A2 ed A3), che abbiamo incrociato con tre linee pure portaseme, diverse per ogni impollinante (B1, B2, B3 per A1, B4, B5, B6 per A2 e B7, B8, B9 per A3). Alla fine abbiamo nove ibridi in tre gruppi, a seconda della linea impollinante.
Il dataset ‘crosses.csv’ riporta i risultati ottenuti con un esperimento a blocchi randomizzati con quattro repliche (36 dati in totale) e può essere caricato dalla solita repository online.
fileName <- "https://www.casaonofri.it/_datasets/crosses.csv"
dataset <- read.csv(fileName, header=T)
head(dataset, 15)
## Male Female Block Yield
## 1 A1 B1 1 9.984718
## 2 A1 B1 2 13.932663
## 3 A1 B1 3 12.201312
## 4 A1 B1 4 1.916661
## 5 A1 B2 1 8.928465
## 6 A1 B2 2 10.513908
## 7 A1 B2 3 10.035964
## 8 A1 B2 4 2.375822
## 9 A1 B3 1 21.511028
## 10 A1 B3 2 21.859852
## 11 A1 B3 3 17.626284
## 12 A1 B3 4 13.966646
## 13 A2 B4 1 17.483089
## 14 A2 B4 2 19.480893
## 15 A2 B4 3 12.83879212.7 Definizione del modello lineare
In questo esperimento, la produzione del mais dipende dal blocco e dall’effetto paterno, mentre l’effetto materno può essere solo determinato entro ogni linea impollinante. Si dice che l’effetto materno è innestato entro l’effetto paterno, come mostrato in Figura 12.3. Pertanto, il modello lineare risulta così definito:
\[Y_{ijk} = \mu + \gamma_k + \alpha_i + \delta_{ij} + \varepsilon_{ijk}\]
dove \(\gamma_k\) è l’effetto del blocco \(k\), \(\alpha_i\) è l’effetto dell’impollinante \(i\) e \(\delta_{ij}\) è l’effetto del portaseme \(j\) entro ogni linea impollinante \(i\). La componente random \(\varepsilon\) viene assunta, come al solito, gaussiana e omoscedastica, con media 0 e deviazione standard uguale a \(\sigma\).
La differenza con un modello ANOVA completamente incrociato dovrebbe essere chiara: in quest’ultimo caso abbiamo due effetti, A, B e la loro interazione A:B, mentre in un modello innestato abbiamo solo l’effetto A e l’effetto B entro A (A/B), mentre l’effetto principale B manca, in quanto non esiste in pratica.

Figura 12.3: Struttura di un disegno sperimentale gerarchico
12.8 Fitting del modello con R
Il modello viene codificato senza l’effetto principale del portaseme, utilizando l’operatore ‘/’.
L’ispezione dei residui viene fatta col metodo grafico usuale; la Figura 12.4 non mostra problemi visibili e quindi si può procedere con la scomposizione della varianza.
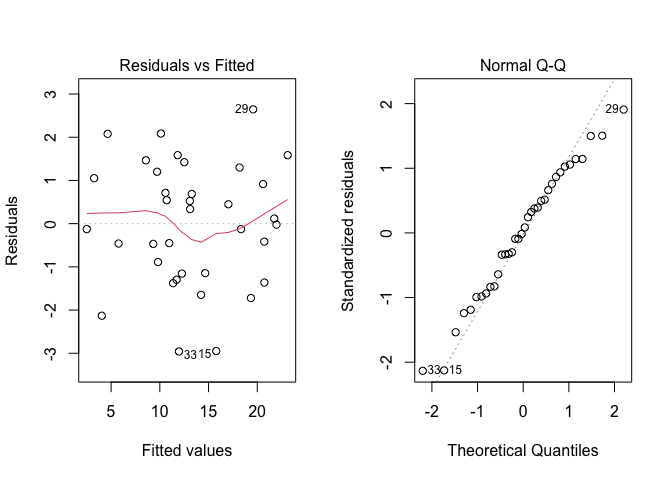
Figura 12.4: Analisi grafica dei residui per un modello ANOVA a due vie, con effetti innestati
anova(mod)
## Analysis of Variance Table
##
## Response: Yield
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(Block) 3 383.75 127.917 44.355 6.051e-10 ***
## Male 2 134.76 67.378 23.363 2.331e-06 ***
## Male:Female 6 575.16 95.860 33.239 1.742e-10 ***
## Residuals 24 69.21 2.884
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La tabella ANOVA mostra che tutti gli effetti sono significativi e, pertanto, possiamo esaminare e confrontare le medie dei diversi ibridi, anche considerando che l’effetto paterno è relativamente poco importante, dato che le linee impollinanti sono incrociate con linee portaseme diverse.
library(emmeans)
mfMeans <- emmeans(mod, ~Female|Male)
multcomp::cld(mfMeans, Letters = LETTERS)
## Male = A1:
## Female emmean SE df lower.CL upper.CL .group
## B2 7.96 0.849 24 6.21 9.72 A
## B1 9.51 0.849 24 7.76 11.26 A
## B3 18.74 0.849 24 16.99 20.49 B
##
## Male = A2:
## Female emmean SE df lower.CL upper.CL .group
## B6 8.72 0.849 24 6.97 10.47 A
## B5 11.23 0.849 24 9.48 12.98 AB
## B4 15.18 0.849 24 13.43 16.93 B
##
## Male = A3:
## Female emmean SE df lower.CL upper.CL .group
## B9 10.11 0.849 24 8.35 11.86 A
## B8 17.73 0.849 24 15.97 19.48 B
## B7 20.12 0.849 24 18.36 21.87 B
##
## Results are averaged over the levels of: Block
## Confidence level used: 0.95
## Results are averaged over some or all of the levels of: Block
## P value adjustment: tukey method for comparing a family of 9 estimates
## significance level used: alpha = 0.05
## NOTE: If two or more means share the same grouping symbol,
## then we cannot show them to be different.
## But we also did not show them to be the same.In conclusione, vediamo che l’analisi dei disegni con due fattori innestati è piuttosto simile a quella per due fattori incrociati, con l’unica eccezione che l’effetto principale per il fattore innestato non è incluso nel modello.