Capitolo 6 Decisioni e incertezza
Nel capitolo precedente abbiamo visto come è possibile esprimere l’incertezza che il campionamente e, in genere, l’errore sperimentale producono sulle nostre stime. In particolare, abbiamo visto che, per una certa statistica rilevata su un campione, è possibile utilizzare la sampling distribution (o sample space o distribuzione campionaria), con un procedimento che prende il nome di inferenza statistica (stima per intervallo). Analogamente, la sampling distribution può essere utilizzata per prendere decisioni in presenza di incertezza, con un procedimento che si chiama test d’ipotesi. Anche in questo capitolo, vediamo alcuni esempi, partendo da quello già esposto in precedenza.
6.1 Confronto tra una media osservata e una media teorica
Nel capitolo precedente, abbiamo misurato la concentrazione di una soluzione erbicida tramite un gascromatografo. Facendo l’analisi in triplicato, abbiamo ottenuto i tre valori riportati di seguito.
## [1] 105.5152 123.3292 133.0133Abbiamo calcolato la media, la deviazione standard, l’errore standard e l’intervallo di confidenza. Ora immaginiamo che esista un livello soglia pari a 200 mg/l, al disopra del quale il prodotto diviene tossico per i mammiferi. Dato che non conosciamo il vero valore di \(\mu\) ci chiediamo: è possibile che le nostre tre repliche, nella realtà, provengano da una popolazione che ha media uguale a 200?
In questo caso sappiamo bene che non è possibile, visto che abbiamo generato i dati sperimentali (vedi il capitolo precedente), tramite simulazione Monte Carlo, partendo da una verità vera nota (\(\mu\) = 120 e \(\sigma\) = 12); tuttavia, nella realtà, la domanda è lecita.
Potremmo formalizzare la nostra domanda mediante un’ipotesi scientifica, detta ipotesi nulla (\(H_0\)), per la quale assumiamo che \(\mu = 200\). Scriviamo:
\[H_0: \mu = 200\]
Cerchiamo ora di vedere quanto la nostra osservazione è ‘discrepante’ rispetto all’ipotesi nulla.
In particolare, possiamo calcolare una statistica, che abbiamo già utilizzato per l’intervallo di confidenza, in grado di misurare questa discrepanza:
\[ T = \frac{m - 200}{s_m} \]
Il valore da noi osservato è:
il che implica un certo grado di discrepanza, altrimenti avremmo dovuto osservare un valore di T più vicino a 0. Possiamo affermare che ciò sia imputabile solo alla variabilità di campionamento e che quindi il nostro esperimento confermi l’ipotesi nulla (\(\mu = 200\))?
È evidente che l’ipotesi nulla, oltre che come l’abbiamo scritta più sopra, potrebbe anche essere posta come:
\[H_0: T = 0\]
Oltre all’ipotesi nulla, dobbiamo anche definire l’ipotesi alternativa semplice (a ‘due code’), che potrebbe essere:
\[H_1: T \neq 0\]
E’possibile anche definire ipotesi alternative complesse del tipo:
\[H_1: T < 0\]
oppure:
\[H_1: T > 0\]
Bisogna ricordare che le ipotesi debbono essere stabilite prima di effettuare l’esperimento. In questo caso abbiamo fatto un campionamento e abbiamo trovato un valore (120.619) inferiore a quello atteso (200). Che cosa ci attendevamo prima di fare l’esperimento? Ci attendevamo un valore diverso da 200, ma non avevamo informazioni per immaginare se avrebbe potuto essere maggiore o minore? In questo caso l’ipotesi alternativa dovrebbe essere la prima (quella semplice). Avevamo invece ragionevoli motivi per ritenere che \(m\) avrebbe potuto essere inferiore, ma non superiore a 200? In questo caso l’ipotesi alternativo potrebbe essere la seconda (ipotesi alternativa complessa). Propendiamo per quest’ultima ipotesi, cioè \(\mu < 200\).
Siamo in totale coerenza con la logica Galileiana: abbiamo un ipotesi di partenza e un esperimento, col quale eventualmente rigettare questa ipotesi ,per abbracciarno una alternativa. Fisher, negli anni 20 del 1900, propose di utilizzare come ‘forza dell’evidenza scientifica’ la probabilità di ottenere un risultato uguale o più estremo di quello osservato, calcolato supponendo vera l’ipotesi nulla. Penso che il modo migliore di spiegare questo concetta è attraverso l’esempio pratico.
6.1.1 Simulazione Monte Carlo
Supponiamo che l’ipotesi nulla sia vera. È evidente che, se prendiamo una popolazione gaussiana con \(\mu = 200\), cominciamo ad estrarre campioni e, per ognuno di essi, calcoliamo T, otterremo un ’ventaglio di valori, che danno origine ad una sampling distribution. Ci chiediamo: come è fatta questa sampling distribution?
La cosa migliore è costruirla con una simulazione Monte Carlo, ripetendo molte volte (es. 100’000) l’estrazione di campioni con numerosità pari a 3, da una distribuzione normale con media pari a 200 e deviazione standard pari a 13.948. Utilizziamo questo valore di deviazione standard perché è quello osservato nel campione e, nella realtà, sarebbe l’unico valore disponibile, dato che non sapremmo nulla della popolazione originale. Per eseguire questa operazione utilizziamo il seguente codice R:
set.seed(1234)
result <- rep(0, 100000)
for (i in 1:100000){
sample <- rnorm(3, 200, s)
result[i] <- (mean(sample) - 200) / (sd(sample)/sqrt(3))
}In questo modo otteniamo 100’000 valori di T e possiamo calcolare la proporzione di questi che è pari o inferiore al valore da noi osservato (1):
Eseguendo questa simulazione, otteniamo una proporzione di valori pari a 0.00517. Il risultato si riassume dicendo che il P-level per l’ipotesi nulla è pari a 0.00517. La regola di condotta della statistica tradizionale è quella di rigettare l’ipotesi nulla quando il P-level è inferiore ad una certa soglia prefissata (normalmente P \(\leq\) 0.05). Di conseguenza, concludiamo che vi sono elementi sufficienti per rifiutare l’ipotesi che il valore incognito della concentrazione di erbicida sia pari a 200 mg/l. Infatti, se l’ipotesi nulla fosse vera, avremmo osservato qualcosa di estremamente improbabile.
In altre parole, l’evidenza scientifica è sufficientemente buona per il rifiuto dell’ipotesi nulla, anche se esiste una certa probabilità d’errore, pari appunto alla probabilità che l’ipotesi nulla sia vera (P = 0.00517).
6.1.2 Soluzione formale
Possiamo definire una distribuzione di frequenze per T? Empiricamente possiamo osservare che, analogamente al caso degli intervalli di confidenza, la distribuzione di riferimento non è normale, bensì t di Student, con due gradi di libertà. Analogamente al caso degli intervalli di confidenza, la gaussiana è una buona approssimazione solo se il campione è molto numeroso o se \(\sigma\) della popolazione è noto.
#Sampling distribution per T
max(result);min(result)
## [1] 545.0709
## [1] -594.9397
b <- seq(-600, 600, by=0.25)
hist(result, breaks = b, freq=F,
xlab = expression(paste(m)), ylab="Density",
xlim=c(-10,10), ylim=c(0,0.45), main="")
curve(dnorm(x), add=TRUE, col="blue")
curve(dt(x, 2), add=TRUE, col="red")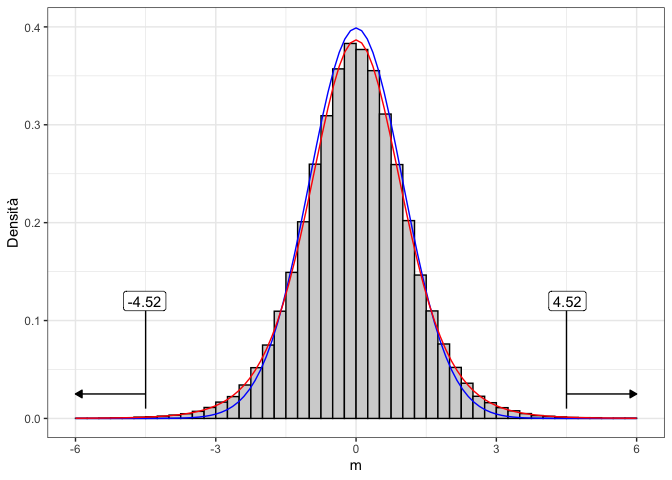
Figure 6.1: Sampling distribution empirica a confronto con una distribuzione normale (in rosso) e una distribuzione t di Student con due gradi di libertà
Senza ricorrere alla simulazione Monte Carlo, possiamo quindi risolvere il problema utilizzando la distribuzione t di Student, nella quale cercheremo la probabilità di ottenere valori di T minori o uguali a quello da noi osservato:
dove gli argomenti indicano rispettivamente il valore osservato. Il P-level è molto simile a quello ottenuto con la simulazione Monte Carlo.
Allo stesso valore, più semplicemente, si giunge utilizzando la funzione “t.test()”:
6.1.3 Interpretazione del P-level
Quando il P-level è inferiore a 0.05, concludiamo che vi sono prove scientifiche sufficientemente forti per rifiutare la nostra ipotesi di partenza.
Bisogna sottolineare come il P-level nella statistica tradizionale sia stato inizialmente proposto da Fisher come criterio di comportamento e non come un vero e proprio criterio inferenziale-probabilistico. Successivamente, Jarzy Neyman ed Egon Pearson, intorno al 1930, proposero di utilizzare il P-level come probabilità di errore di I specie, cioè come probabilità di rifiutare erroneamente l’ipotesi nulla. Tuttavia, trattandosi di una probabilità calcolata a partire da una sampling distribution, cioè da un’ipotetica infinita ripetizione dell’esperimento, essa non ha alcun valore in relazione al singolo esperimento effettivamente eseguito, come i due autori menzionati in precedenza hanno esplicitamente chiarito.
Di conseguenza, nel caso in esempio, affermare che abbiamo una probabilità di errore pari a 0.0051 nel rifiutare l’ipotesi nulla, rappresenterebbe un abuso: le nostre conclusioni potrebbero essere false o vere, ma non abbiamo alcun elemento per scegliere tra le due opzioni. Possiamo solo affermare che, se ripetessimo infinite volte l’esperimento e se l’ipotesi nulla fosse vera, otterremmo un risultato estremo come il nostro o più estremo solo in 5 casi (circa) su 1000. In altre parole, nel lungo periodo, basando le nostre conclusioni sul criterio anzidetto (rifiuto l’ipotesi nulla se il P-value è inferiore a 0.05) commettiamo un errore in non più del 5% dei casi. Insomma, il P-level non può essere guardato come la probabilità di ‘falso-positivo’ ad ogni singolo test, ma solo nel lunghissimo periodo.
6.2 Confronto tra due medie: il test t di Student
Un ricercatore ha scelto casualmente dieci piante da una popolazione; ne ha trattate cinque con l’erbicida A e cinque con il placebo P. Alla fine dell’esperimento ha determinato il peso di ognuna delle dieci piante. E’ evidente che le piante in prova sono solo un campione di quelle possibili, così come è evidente che il peso, come ogni altra variabile biologica, è soggetto ad una certa variabilità naturale, legata sia a questioni genotipiche che fenotipiche, oltre che ad eventuali errori casuali di misura.
I risultati sono i seguenti:
Nel campione A la media è pari a 70.2, mentre la deviazione standard è pari a 4.87. L’errore standard è pari a 2.18 e quindi l’intervallo di confidenza della media è 70.2 \(\pm\) 6.04. Invece, nel campione P, la media è 85.4, mentre la deviazione standard è pari a 5.72. L’errore standard è pari a 2.56, mentre l’intervallo di confidenza per la media è 85.4 \(\pm\) 7.11
Possiamo affermare che l’erbicida A riduce il peso delle piante trattate, coerentemente con le aspettative riguardo ad una molecola di questo tipo? Nel rispondere a questa domanda bisogna tener presente che i campioni sono totalmente irrilevanti, dato che il nostro interesse è rivolto alle popolazioni che hanno generato i campioni. Vogliamo cioè che le nostre conclusioni abbiano carattere di universalità e non siano specifiche a quanto abbiamo osservato nel nostro esperimento. Intanto possiamo notare che il limite di confidenza superiore per A (70.2 + 6.04 = 76.24) è inferiore al limite di confidenza inferiore per P (75.4 - 7.11 = 68.29). Questo non è un criterio sul quale basare le nostre considerazioni, ma è comunque un segno che le popolazioni da cui provengono i due campioni potrebbero essere diverse.
Per trovare un criterio decisionali più rigoroso, possiamo formulare l’ipotesi nulla in questi termini:
\[H_0: \mu_1 = \mu_2 = \mu\]
In altre parole, la nostra ipotesi di lavoro è che i due campioni siano in realtà estratti da due distribuzioni normali con la stessa media e la stessa deviazione standard, il che equivale a dire che essi provengono da un’unica distribuzione normale con media \(\mu\) e deviazione standard \(\sigma\).
L’ipotesi alternativa semplice può essere definita:
\[H_1 :\mu_1 \ne \mu_2\]
Se avessimo elementi sufficienti già prima di effettuare l’esperimento (e non dopo aver visto i risultati), potremmo anche adottare ipotesi alternative complesse, del tipo
\[H_1 :\mu _1 > \mu _2\]
oppure:
\[H_1 :\mu _1 < \mu _2\]
Quale statistica potrebbe meglio descrivere l’andamento dell’esperimento, in relazione all’ipotesi nulla? E’ evidente che questa statistica dovrebbe essere basata su due indicatori diversi:
- l’entità della differenza tra le medie: più la differenza tra le due medie è alta e più è probabile che essa sia significativa;
- l’entità dell’errore standard. Più è elevata la variabilità dei dati (e quindi l’errore di stima) più è bassa la probabilità che le differenze osservate tra le medie siano significative.
Su queste basi, si può individuare la seguente statistica:
\[T = \frac{m_1 - m_2}{SED}\]
Si può osservare che T, in realtà, non è altro che il rapporto tra le quantità indicate in precedenza ai punti 1 e 2: infatti la quantità al numeratore è la differenza tra le medie dei due campioni, mentre la quantità al denominatore è il cosiddetto errore standard della differenza tra due medie (SED). Quest’ultima quantità si può ottenere pensando che i due campioni sono estratti in modo indipendente e, pertanto, la varianza della somma (algebrica) è uguale alla somma delle varianze. La varianza delle due medie è data dal quadrato delle loro deviazioni standard, cioè dal quadrato degli errori standard (SEM). Pertanto:
\[SED^2 = SEM_1^2 + SEM_2^2\]
Sappiamo anche che il SEM si ottiene dividendo la deviazione standard di ogni campione per la radice quadrata del numero dei dati, quindi:
\[SED^2 = \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\]
cioè:
\[SED = \sqrt{ \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }\]
Possiamo anche scrivere:
\[SED = \sqrt{ \frac{s_1^2 \, n_2 + s_2^2 \, n_1}{n_1 \, n_2} }\]
e, se le varianze sono uguali (\(s_1^2 = s_2^2 = s^2\)), segue che:
\[SED = \sqrt {s^2 \frac{n_1 + n_2}{n_1 \, n_2 } }\]
Se fosse anche \(n_1 = n_2 =n\), potremmo scrivere:
\[SED = \sqrt{2 \, \frac{s^2}{n} } = \sqrt{2} \times SEM\]
Il valore osservato per T è quindi uguale a:
\[T = \frac{85.4 - 70.2}{3.361547} = 4.5217\]
dove il denominatore è ottenuto come:
\[SED = \sqrt{ 2.18^2 + 2.56^2 } = 3.361547\]
A questo punto avendo osservato T = 4.5217, possiamo chiederci: qual è la ‘sampling distribution’ per T, cioè quali valori potrebbe assumere questa statistica se ripetessimo il campionamento infinite volte, assumendo che l’ipotesi nulla fosse vera?
La sampling distribution per T potrebbe essere ottenuta empiricamente, utilizzando una simulazione Monte Carlo. Il codice da utilizzare per questa simulazione è fornito in appendice, dove si può vedere che, formalmente, la sampling distribution per T è una distribuzione t di Student, con 8 gradi di libertà (quattro per campione). Siamo quindi in grado di calcolare la probabilità di ottenere valori di T altrettanto estremi o più estremi di quello da noi osservato, tenendo però presente che il test è ‘a due code’. Infatti, il T osservato è positivo, ma solo perché abbiamo scritto la differenza come \(m_2 - m_1\) invece che come \(m_1 - m_2\). Tuttavia, entrambe le differenze sono possibili, quindi dobbiamo considerare anche il valore reciproco -T. In altre parole, ci chiediamo qual è la possibilità di campionare da una distribuzione t di Student valori esterni all’intervallo (-4.5217; 4.5217). La risposta, con R, è piuttosto semplice da ottenere:
Abbiamo moltiplicato per 2 il risultato, in quanto la funzione ‘dt()’ fornisce la probabilità di trovare individui inferiori a -4.5217 (‘lower.tail = T’). Essendo la distribuzione simmetrica, la probabilità di trovare soggetti superiori a 4.5217 è esattamente la stessa.
Vediamo che il P-level è minore di 0.05 e possiamo quindi rifiutare l’ipotesi nulla. Concludiamo che vi è un’evidenza scientifica abbastanza forte per ritenere che l’erbicida A induca una riduzione del peso delle piante trattate.
Allo stesso valore, più semplicemente, si perviene utilizzando la funzione:
t.test(A, P, var.equal=T)
##
## Two Sample t-test
##
## data: A and P
## t = -4.5217, df = 8, p-value = 0.001945
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -22.951742 -7.448258
## sample estimates:
## mean of x mean of y
## 70.2 85.4Gli argomenti della funzione ‘t.test()’ sono i due vettori è l’argomento ‘var.equal’, che in questo caso è stato settato su TRUE. Chi volesse comprendere meglio il motivo di questa specifica, può leggerlo in appendice, alla fine del capitolo. Per gli altri, precisiamo solo che il test di t così eseguito è valido quando i due campioni sono indipendenti ed estratti da distribuzioni gaussiane con la stessa varianza. Queste assunzioni, soprattutto la seconda, sono sostenibili solo se le varianze osservate per i due campioni sono molto simili, con una differenza al di sotto di un ordine di grandezza, come accade nel nostro esempio.
6.3 Confronto tra due proporzioni: il test \(\chi^2\)
Il test di t è molto utile, ma soltanto nel caso in cui si abbia a che fare con caratteri quantitativi, cioè con variabili misurate su una scala continua, per le quali sia possibile calcolare statistiche descrittive, come appunto la media. Talvolta, i ricercatori sono interessati a rilevare caratteristiche qualitative, come ad esempio lo stato di una pianta in seguito ad un trattamento (morta o viva), il colore dei semi (si ricordino i piselli verdi e gialli di Mendel) ed altre caratteristiche che non sono misurabili su una scala continua.
Avendo a che fare con variabili qualitative, l’unica statistica rilevabile è il numero di soggetti che presentano le diverse modalità. Ad esempio, immaginiamo un esperimento per verificare se un coadiuvante aumenta l’efficacia di un insetticida. In questo esperimento, utilizziamo l’insetticida da solo e miscelato con il coadiuvante su due gruppi di insetti diversi. Nel primo gruppo (trattato con insetticida) contiamo 56 morti su 75 insetti trattate, mentre nel secondo gruppo (trattato con insetticida e coadiuvante) otteniamo 48 morti su 50 insetti trattati.
I risultati di questo esperimento si riducono ad una tabella di contingenza:2
counts <- c(56, 19, 48, 2)
tab <- matrix(counts, 2, 2, byrow = T)
row.names(tab) <- c("I", "IC")
colnames(tab) <- c("M", "V")
tab
## M V
## I 56 19
## IC 48 2Per una tabella di contingenza, possiamo determinare una statistica che misura la connessione tra variabili (trattamento e mortalità), detta \(\chi^2\). La connessione è l’indicatore giusto per rispondere alla nostra domanda di ricerca; infatti ci stiamo chiedendo se la proporzione dei morti è indipendente dal tipo di trattamento oppure no.
Con R, il \(\chi^2\) si calcola applicando la funzione summary all’oggetto ‘data.table’. Dato che la nostra tabella ‘tab’ è, in realtà, una matrice (almeno così come l’abbiamo creata), prima di interrogarla con il metodo ‘summary()’ dobbiamo trasformarla in un oggetto ‘data.table’, con la funzione ‘as.table()’:
summary( as.table(tab) )
## Number of cases in table: 125
## Number of factors: 2
## Test for independence of all factors:
## Chisq = 9.768, df = 1, p-value = 0.001776Il valore di \(\chi^2\) osservato è pari a 9.768, il che indica un certo grado di connessione. Infatti, ricordiamo che, in caso di indipendenza tra le variabili, \(\chi^2\) dovrebbe essere zero. Tuttavia, noi non siamo interessati ai due campioni, in quanto i 125 soggetti osservati sono tratti da due popolazioni più ampie. Considerando queste due popolazioni, poniamo l’ipotesi nulla in questi termini:
\[H_o :\pi_1 = \pi_2 = \pi\]
Vediamo che, come negli altri esempio, l’ipotesi nulla riguarda i parametri delle popolazioni (\(\pi_1\) e \(\pi_2\)), non quelli dei campioni (\(p_1\) e \(p_2\)). Ci chiediamo: se l’ipotesi nulla è vera (\(\pi_1 = \pi_2\)), qual è la sampling distribution per \(\chi^2\)? E soprattutto, quanto è probabile ottenere un valore alto come il nostro o più alto?
In appendice mostriamo come si possa arrivare a questo risultato con una simulazione Monte Carlo. In modo formale, si può dimostrare che, se \(n\) è sufficientemente grande (n > 30), il valore osservato di \(\chi^2\) segue appunto la distribuzione di probabilità \(\chi^2\), con un numero di gradi di libertà \(\nu\) pari al numero dei dati indipendenti, che, in questo caso, è pari ad 1. Infatti, una volta fissata una frequenza, le altre sono automaticamente definite, dovendo restituire i totali marginali. In R, possiamo utilizzare la funzione ‘pchi()’ per calcolare la probabilità di ottenere valori pari o superiori a 9.768:
Allo stesso risultato, ma in modo più semplice, è possibile pervenire utilizzando la già citata funzione ‘summary()’, applicata alla tabella di contingenza (vedi sopra), oppure:
chisq.test(tab, correct = F)
##
## Pearson's Chi-squared test
##
## data: tab
## X-squared = 9.768, df = 1, p-value = 0.001776Come nel caso del ‘t’ di Student, abbiamo diversi tipi di test di chi quadro. In particolare, possiamo applicare o no la correzione per la continuità, che è necessaria quando il numero dei soggetti è piccolo (minore di 30, grosso modo),. Nel nostro caso, non lo abbiamo ritenuto necessario ed abbiamo quindi aggiunto l’argomento ‘correct = F’.
6.4 Conclusioni
Abbiamo visto quale strumento abbiamo a disposizione per tirare conclusioni in presenza di incertezza sperimentale. Dovrebbe essere evidente che anche le nostre conclusioni sono incerte, in quanto soggette all’errore di campionamento. In particolare, abbiamo visto che esiste un rischio di errore di prima specie, cioè rifiutare erronamente l’ipotesi nulla (falso positivo). Allo stesso modo, esiste anche un rischio di errore di II specie, cioè accettare erroneamente l’ipotesi nulla (falso negativo). Di questi due tipi di errore abbiamo parlato più diffusamente in appendice.
6.5 Riepilogo
Lo schema di lavoro, nel test d’ipotesi, è il seguente:
- Si formula l’ipotesi nulla;
- Si individua una statistica che descriva l’andamento dell’esperimento, in relazione all’ipotesi nulla;
- Si individua la sampling distribution per questa statistica, assumendo vera l’ipotesi nulla; la sampling distribution può essere empirica (ottenuta per simulazione) o teorica, scelta in base a considerazioni probabilistiche
- Si calcola la probabilità che, essendo vera l’ipotesi nulla, si possa osservare una valore altrettanto estremo o più estremo di quello calcolato, per la statistica di riferimento;
- Se il livello di probabilità è inferiore ad una certa soglia \(\alpha\) prefissata (generalmente 0.05), si rifiuta l’ipotesi nulla.
6.6 Esercizi
- Uno sperimentatore ha impostato un esperimento verificare l’effetto di un fungicida (A) in confronto al testimone non trattato (B), in base al numero di colonie fungine sopravvissute. Il numero delle colonie trattate è di 200, con 180 colonie sopravvissute al trattamento. Il numero di quelle non trattate è di 100, con 50 colonie sopravvissute. Stabilire se i risultati possono essere considerati significativamente diversi, per un livello di probabilità del 5%
- Uno sperimentatore ha impostato un esperimento per confrontare due tesi sperimentali (A, B). Per la tesi A sono stati osservate le seguenti produzioni: 9.3, 10.2, 9.7. Per la tesi B, sono state osservati valori di 12.6, 12.3 e 12.5. Stabilire se i risultati possono essere considerati significativamente diversi, per un livello di probabilità del 5%.
- Uno sperimentatore ha impostato un esperimento per confrontare se l’effetto di un fungicida è significativo, in un disegno sperimentale con tre ripetizioni. Con il trattamento, i risultati produttivi (in t/ha) sono 65, 71 e 68. Con il non trattato, i risultati sono 54, 51 e 59. E’significativo l’effetto del trattamento fungicida sulla produzione, per un livello di probabilità di errore del 5%?
- Immaginate di aver riscontrato che, in determinate condizioni ambientali, 60 olive su 75 sono attaccate da Daucus olee (mosca dell’olivo). Nelle stesse condizioni ambientali, diffondendo in campo un insetto predatore siamo riusciti a ridurre il numero di olive attaccate a 12 su 75. Si tratta di una oscillazione casuale del livello di attacco o possiamo concludere che l’insetto predatore è stato un mezzo efficace di lotta biologica alla mosca dell’olivo?
6.7 Per approfondire un po’…
6.7.1 Tipologie alternative di test t di Student
Chiunque abbia utilizzato un computer per eseguire un test di t, si sarà accorto che è necessario scegliere tra tre procedure alternative. Infatti, abbiamo:
- t-test appaiato. In questo caso le misure sono prese a coppia sullo stesso soggetto e non sono quindi indipendenti.
- t-test omoscedastico. Le misure sono prese su soggetti diversi (indipendenti) e possiamo suppore che i due campioni provengano da due popolazioni con la stessa varianza.
- t-test eteroscedastico. Le misure sono prese su soggetti diversi, ma le varianze non sono omogenee.
Consideriamo i due campioni:
C1
## [1] 12.660770 9.947017 10.500794 13.471233 13.459139
C2
## [1] 16.14014 16.20918 12.96391 15.51307 14.91213
mean(C1)
## [1] 12.00779
mean(C2)
## [1] 15.14769
var(C1)
## [1] 2.798071
var(C2)
## [1] 1.767402Vediamo che le medie sono diverse ma le varianze sono simili, dello stesso ordine di grandezza. Pertanto, possiamo utilizzare un test t omoscedastico, che garantisce un più alto livello di potenza.
t.test(C1, C2, var.equal = T, paired = F)
##
## Two Sample t-test
##
## data: C1 and C2
## t = -3.2859, df = 8, p-value = 0.01109
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -5.3434208 -0.9363712
## sample estimates:
## mean of x mean of y
## 12.00779 15.14769Consideriamo invece quest’altra coppia di campioni:
D1
## [1] 12.06608 11.79470 11.85008 12.14712 12.14591
D2
## [1] 35.14014 35.20918 31.96391 34.51307 33.91213
mean(D1)
## [1] 12.00078
mean(D2)
## [1] 34.14769
var(D1)
## [1] 0.02798071
var(D2)
## [1] 1.767402In questo caso le varianza sono molto diverse e l’assunzione di omoscedasticità non è tenibile. Dobbiamo utilizzare un test eteroscedastico e, di conseguenza, mentre il SED si calcola con la formula esposta più sopra, si pone il problema di stabilire il numero di gradi di libertà del SED stesso. Dato che il sed è ottenuto come somma di varianze, il numero di gradi di libertà può essere approssimato con la formula di Satterthwaite:
\[DF_s \simeq \frac{ \left( s^2_1 + s^2_2 \right)^2 }{ \frac{(s^2_1)^2}{DF_1} + \frac{(s^2_2)^2}{DF_2} }\]
Vediamo che se le varianze e i gradi di libertà sono uguali, la formula precedente riduce a:
\[DF_s = 2 \times DF\]
Nel nostro caso:
In effetti:
t.test(D1, D2, var.equal=F)
##
## Welch Two Sample t-test
##
## data: D1 and D2
## t = -36.959, df = 4.1266, p-value = 2.326e-06
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -23.79070 -20.50312
## sample estimates:
## mean of x mean of y
## 12.00078 34.14769Se le misure in D1 e D2 fossero state rilevate sugli stessi soggetti (due misure per soggetto), allora avremmo cinque soggetti invece che dieci e, di conseguenza solo 4 gradi di libertà:
t.test(D1, D2, var.equal=F, paired=T)
##
## Paired t-test
##
## data: D1 and D2
## t = -38.002, df = 4, p-value = 2.864e-06
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -23.76497 -20.52885
## sample estimates:
## mean of the differences
## -22.146916.7.2 Simulazione del P-value nel test d’ipotesi
Più sopra abbiamo visto che il test d’ipotesi viene eseguito sulla base del principio che, quando l’ipotesi nulla è vera, una statistica campionaria (T, \(\chi^2\) o altro) mostra una certa variabilità tra un campionamento e l’altro. Quando i campionamenti sono tanti (meglio, infiniti), i valori ottenuti danno origine ad una sampling distribution, che può essere modellizzata utilizzando una qualche distribuzione di probabilità formale, come il t di Student il chi quadro e così via.
Invece che ricorrere ad una distribuzione di probabilità nota, possiamo costruire una sampling distribution empirica, utilizzando le simulazioni Monte Carlo. In questo caso, il campionamento viene ripetuto molte volte, assumendo che l’ipotesi nulla sia vera. Mostriamo ora come questo approccio possa essere utilizzato per confrontare due medie oppure due proporzioni campionarie.
Immaginiamo di avere i due campioni, A e P, indicati in precedenza, con un T osservato pari a -4.521727. Se i due campioni fossero estratti dalla stessa popolazione normale, questa dovrebbe avere una media pari a (70.2 + 85.4)/2 = 77.8 e una deviazione standard pari alla deviazione standard delle dieci osservazioni (tutte insieme, senza distinzioni di trattamento), cioè 9.45.
Proviamo ora ad utilizzare un generatore di numeri casuali gaussiani per estrarre numerose (100’000) coppie di campioni, e calcolare, per ogni coppia, il valore T, come abbiamo fatto con la nostra coppia iniziale.
Il codice da utilizzare in R per le simulazioni è il seguente:
T_obs <- -4.521727
set.seed(34)
result <- rep(0, 100000)
for (i in 1:100000){
sample1 <- rnorm(5, media, devSt)
sample2 <- rnorm(5, media, devSt)
SED <- sqrt( (sd(sample1)/sqrt(5))^2 +
(sd(sample2)/sqrt(5))^2 )
result[i] <- (mean(sample1) - mean(sample2)) / SED
}
length(result[result < T_obs]) / 100000
## [1] 0.00095
length(result[result > - T_obs]) /100000
## [1] 0.00082Possiamo notare che, dei 100’000 valori di T osservati assumendo vera l’ipotesi nulla, meno dell’un per mille sono inferiori a quello da noi osservato e altrettanti sono superiori al suo reciproco (4.5217). In totale, la probabilità di osservare un valore di T così alto in valore assoluto e dello 0.18 %, molto simile a quella ottenuta più sopra con il test t di Student.
E se dobbiamo confrontare due proporzioni? Prendiamo la tabella di contingenze utilizzata più sopra:
La connessione si esprime con la statistica chi quadro e il valore osservato è 9.768. Qual è la probabilità che, se i caratteri sono indipendenti, si produca un valore di chi quadro pari o superiore a 9.768?
Per la simulazione possiamo utilizzare la funzione ‘r2dtable()’, che produce il numero voluto di tabelle di contingenza, con righe e colonne indipendenti, rispettando i totali marginali voluti. Le tabelle prodotte (nel nostro caso 10’000) sono restituite come lista, quindi possiamo utilizzare la funzione ‘lapply()’ per applicare ad ogni elemento della lista la funzione che restituisce il \(\chi^2\) (‘chiSim’).
chiSim <- function(x) summary(as.table(x))$stat
set.seed(1234)
tabs <- r2dtable(10000, apply(tab, 1, sum), apply(tab, 2, sum))
chiVals <- as.numeric( lapply( tabs, chiSim) )
length(chiVals[chiVals > 9.768])
## [1] 19Vediamo che vi sono 19 valori più alti di quello da noi osservato, quindi il p-value è 0.0019. Anche in questo caso molto simile a quello ottenuto con un test statistico formale.
6.7.3 Altre letture
- Hastie, T., Tibshirani, R., Friedman, J., 2009. The elements of statistical learning, Springer Series in Statistics. Springer Science + Business Media, California, USA.
da Wikipedia: Le tabelle di contingenza sono un particolare tipo di tabelle a doppia entrata (cioè tabelle con etichette di riga e di colonna), utilizzate in statistica per rappresentare e analizzare le relazioni tra due o più variabili. In esse si riportano le frequenze congiunte delle variabili↩︎